直线渲染算法

概述

目前直线渲染算法主要分为五种：

• 朴素算法
• DDA(Digital Differential Analyzer)算法
• Bresenham算法
• Xiaolin Wu算法
• Gupta-Sproull算法
  Xiaolin Wu算法和Gupta-Sproull算法主要解决直线渲染抗锯齿的问题，意义不大，暂时搁置。下面详细介绍主流算法：DDA和Bresenham算法。

朴素算法

直接根据微分方程计算，源代码如下：

//plot (x1,y1) to (x2,y2)
//x1,y1,x2,y2 是整型

double dx=x2-x1;     //由于要做乘除法，所以使用double型
double dy=y2-y1;
double k=dy/dx;
for(int x=x1；x<=x2;x++)   //逐像素
{
   y=k*x+x1;                
   drawPixel(x,round(y))
}

如下图所示：网格上每个点代表像素点，蓝色的点代表被渲染的点。当k绝对值小于1时(左图)，较为正常，但当k的绝对值大于1时(右图），会造成像素点过于稀疏（左侧）。此时，交换x，y即可（右侧）。

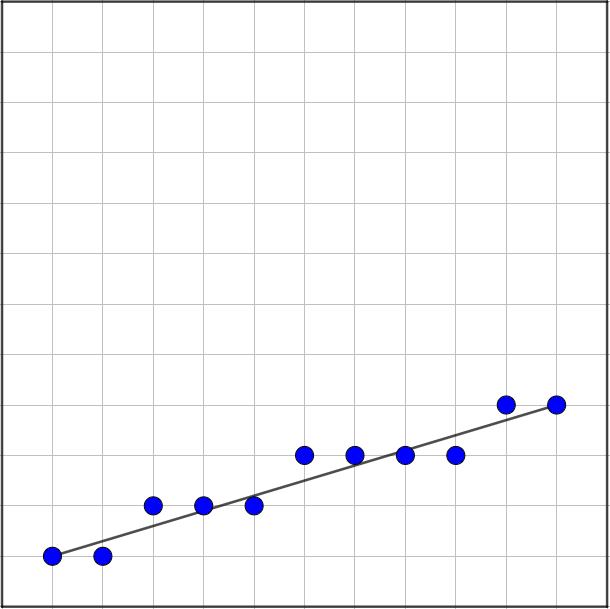
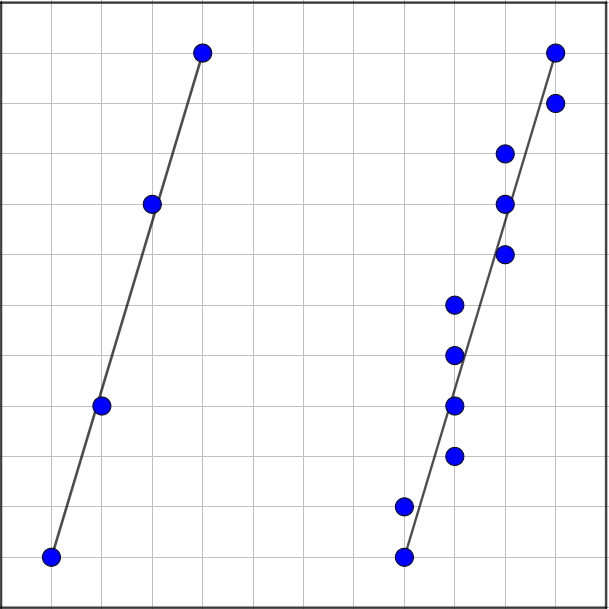
DDA算法

DDA算法实际上就是综合考虑了斜率绝对值小于1以及大于等于1的情况，源代码如下：

//plot (x1,y1) to (x2,y2)
//x1,y1,x2,y2 是整型
double dx=x2-x1;     //由于要做乘除法，所以使用double型
double dy=y2-y1;
double step;
if(abs(dx)>abs(dy)) step=abs(dx);
else                step=abs(dy);
dx=dx/step;
dy=dy/step;
int i=0;
while(i<step)
{
   drawPixel(round(x),round(y));
   x+=dx;
   y+=dy;
   i++;
}

Bresenham算法

Bresenham算法主要解决DDA算法中使用浮点数运算的问题。由于浮点数运算速度比整数运算要慢,所以为提高效率，Bresenham算法只使用整数运算。Bresenham算法将直线分为八个计算域，如下图左。首先需要说的的是：对于任意一条直线，可以把平面分为两个部分，对于两个相邻的像素点，如果它们的中间点，在直线下方，则渲染上面的像素；如果中间点在直线上方，则渲染下面的像素。如下图右，可以看到中间点 \((x_k,y_k+\frac{1}{2})\) 在直线下方，则应该渲染像素点 \((x_k,y_k+1)\) 。

如上图（右）所示，当已知一条直线，以及两个相邻的像素点，那么可以求解两个像素点的中点，接下来判断中间点在直线上面还是下面，来决定渲染哪一个像素点。由于不能使用浮点数，在计算过程中，在不影响结果的情况下，可以将浮点数转化为整数进行运算。
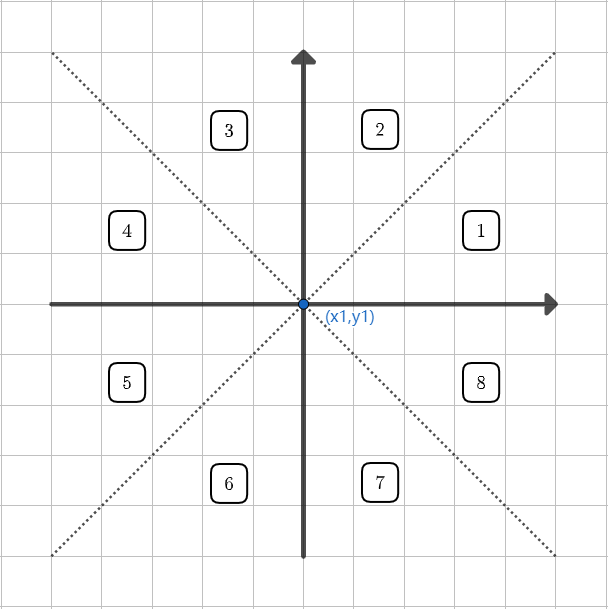
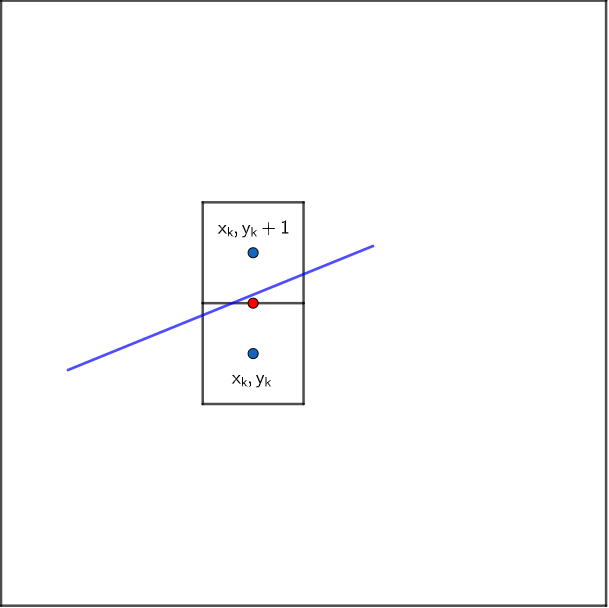
已知直线：起点$(x_0,y_0)$，终点$(x_n,y_n)$，渲染该直线。可以得到直线方程 :$f(x,y)=(y_n-y_0)(x-x_0)-(x_n-x_0)(y-y_0)=0$,化为一般形式$f(x,y)=Ax+By+C=0$.
其中$A=y_n-y_0=dy,B=-(x_n-x_0)=-dx,C=y_0x_n-y_nx_0$.
在第1个计算域中，直线斜率小于1，所以如果第k个被渲染的像素点为$(x_k,y_k)$，那么下一个像素点为$(x_k+1,y_k)$或者$(x_k+1,y_k+1)$。接下来通过中心点$(x_k,y_k+\frac{1}{2})$ 来判断渲染哪一个像素点。若$f(x_k+1,y_k+\frac{1}{2})>0$,则渲染$(x_k+1,y_k+1)$，否则渲染$(x_k+1,y_k)$。那么接下来的问题是如何判断$f(x_k+1,y_k+\frac{1}{2})$的符号。
记$D_k=2f(x_k+1,y_k+\frac{1}{2})$，注意到$f(x_0,y_0)=0$,即$D_0=2f(x_0+1,y_0+\frac{1}{2})=2A+B$。
$\delta{D}=D_{k+1}-D_{k}=2A(x_{k+1}-x_{k})+2B(y_{k+1}-y_{k})=2A+2B(y_{k+1}-y_{k})$,则可得： $$ \displaylines{ D_0=2A+B \\ \delta{D}=D_{k+1}-D_{k}= \begin{cases} 2A, \quad D_k<0即y_{k+1}=y_k \\ 2A+2B, \quad D_k>=0即y_{k+1}=y_k+1 \end{cases} } $$ 则第一个象限代码为：

//plot from (x0,y0) to (xn,yn)
int a=yn-y0;
int b=-(xn-x0);
int d=2*a+b;
int x=x0,y=y0;
while(x<xn)
{
  if(d>=0)
  {
     drawPixel(++x,++y);
     d+=2a+2b;
     y++;
  }else
  {
    drawPixel(++x,y);
    d+=2a;
  }
}

Reference

1. Line drawing algorithm Wiki
2. WhatWhenHow