基础算法模板
基础算法
筛法
埃氏筛
核心思想：只要碰到素数，就将其倍数都筛掉，会有重启筛的情况
时间复杂度：\(O(nloglogn)\)
#include<bits/stdc++.h>
using namespace std;
int n = 0;
bool a[50000010] = {};
int main()
{
scanf("%d", &n);
for(int i=2; i<=n; i++)
{
if(a[i] == 0)
{
for(int j=i; j<=n/i; j++) a[i*j] = 1;
}
}
for(int i=2; i<=n; i++)
if(a[i] == 0) printf("%d\n", i);
}
线性筛
核心思想：
任何合数都可以唯一表示为最小质因数与其他因数的乘积
基于以上原理，我们设计算法，使每个合数只被他的最小质因数筛掉
时间复杂度：\(O(n)\)
#include <bits/stdc++.h>
using namespace std;
/*
线性筛
核心思想：
任何合数都可以唯一表示为最小质因数与其他因数的乘积
基于以上原理，我们设计算法，使每个合数只被他的最小质因数筛掉
*/
int n = 0;
int prim[50000000] = {}, cnt = 0; //prim存储所有素数，cnt为素数的数量
bool notprim[50000000] = {}; //notprim[i]标记i不是素数
int main()
{
scanf("%d", &n);
for(int i=2; i<=n; i++)
{
if(!notprim[i]) prim[++cnt] = i;
for(int j=1; j<=cnt; j++)
{
if(i * prim[j] > n) break;
notprim[i * prim[j]] = true;
//prim[j]即为i的最小质因数
//j后面的质数就没必要再乘了
//比如：当i=9时，此时prim的值为2/3/5/7
//当prim[j]=3时，跳出循环，后面的就不需要再处理了
//假如再处理个5*9,标记上45，但45应该被3*15标记，即i=15时处理
if(i % prim[j] == 0) break;
}
}
for(int i=1; i<=cnt; i++)
{
printf("%d\n", prim[i]);
}
return 0;
}
分治
整数二分
bool check(int x) //检查x是否满足某种性质
int l = 1, r = n, ans = 0;
while(l <= r)
{
int mid = (l+r)>>1;
if(check(mid)) { ans = mid; r = mid - 1; }
else l = mid + 1;
}
printf("%d", ans);
浮点数二分
bool check(double x) //检查x是否满足某种性质
double l = 1, r = n;
while(l + eps < r)
{
double mid = (l+r)/2;
if(check(mid)) r = mid;
else l = mid;
}
printf("%lf", l);
//或者写成这样
double l = 1, r = n;
for(int i=1; i<=100; i++)
{
double mid = (l+r)/2;
if(check(mid)) r = mid;
else l = mid;
}
printf("%lf", l);
蒙哥马利快速幂取模算法
void merge_sort(int q[], int l, int r)
{
typedef long long ll;
ll montgomery(ll a, ll b, ll c)
{
ll ans = 1;
a = a % c;
while(b > 0)
{
if(b & 1) ans = (ans * a) % c;
b = b >> 1;
a = a * a % c;
}
return ans;
}
排序算法
排序的稳定性是指排序完成后，相等数字的相对位置是否改变，不改变则是稳定排序，改变则是不稳定排序。
稳定排序：
插入排序
桶排序
归并排序
不稳定排序：
快速排序
快速排序
原理： 通过分治的方式将一个数组排序
快排分为三个过程：
1、将数列划分为两部分（要求保证相对大小关系）
2、递归到两个子序列中分别进行快速排序
3、不用合并，因为此时数列已经完全有序
时间复杂度： 快排的最优时间复杂度和平均时间复杂度为\(O(nlogn)\),最坏时间复杂度为\(O(n^2)\)
稳定性： 快排是一种不稳定的排序算法。
例题：
P1177 【模板】排序
https://www.luogu.com.cn/problem/P1177
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n = 0;
int a[maxn] = {};
void qsort(int q[], int l, int r)
{
if(l >= r) return;
int i = l - 1, j = r + 1;
int x = q[(l + r) >> 1]; //阈值
while(i < j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
qsort(q, l, j);
qsort(q, j+1, r);
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
qsort(a, 1, n);
for(int i=1; i<=n; i++) printf("%d ", a[i]);
return 0;
}
插入排序
原理： 将待排序元素划分为“已排序”和“未排序”两部分，每次从“未排序”元素中选择一个插入到“已排序”的元素中的正确位置。
时间复杂度：
最优时间复杂度为\(O(n)\)，在数列几乎有序时效率很高。
最坏时间复杂度和平均时间复杂度都为\(O(n^2)\)
稳定性： 插入排序是一种稳定的排序算法。
例题：
该题用插入排序，有些点会TLE
P1177 【模板】排序
https://www.luogu.com.cn/problem/P1177
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n = 0;
int a[maxn] = {};
//插入排序
void insort(int arr[], int cnt)
{
for(int i=2; i<=cnt; i++)
{
int key = a[i]; //将a[i]的值记录下来
int j = i - 1;
//从i-1开始往前找，找到第一个小于a[i]值的位置j
//如果大于a[i]则不断往后移
while(j >= 1 && arr[j] > key)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
insort(a, n);
for(int i=1; i<=n; i++) printf("%d ", a[i]);
return 0;
}
桶排序
桶排序适用于待排序数据值域较大但分布比较均匀的情况
排序过程：
1、直接设置n个桶，求出每个桶可放元素的范围
2、遍历序列，将元素一个个放到对应的桶中
3、对每个不是空的桶进行排序（插入排序）
4、从不是空的桶里把元素再放回原来的序列中
时间复杂度：
桶排序的平均时间复杂度为\(O(n+n^2/k+k)\)(将值域平均分成\(n\)块+排序+重新合并元素)，当k≈n时为\(O(n)\)
桶排序的最坏时间复杂度为\(O(n^2)\)
稳定性： 最后的桶排序是一种稳定的，如果桶内排序使用插入排序，则整体是稳定的。
ps: 分成\(n\)个桶是按值域分的，不是按元素的个数
例题：
P1177 【模板】排序
https://www.luogu.com.cn/problem/P1177
#include <bits/stdc++.h>
using namespace std;
/*
直接开n个桶就行，因为这样时间复杂度最低
*/
const int maxn = 1e5 + 10;
int n = 0;
int a[maxn] = {};
vector<int> b[maxn];
//插入排序
void insort(vector<int> &v)
{
for(int i=1; i<v.size(); i++)
{
int key = v[i];
int j = i - 1;
while(j >= 0 && v[j] > key)
{
v[j+1] = v[j];
j--;
}
v[j+1] = key;
}
}
void bucketsort()
{
//直接按值域开n个桶
//求出每个桶可以放的数量，方便后边求每个元素应该放到哪个桶中
int size = 1e9 / n + 1;
//将每个元素放到不同的桶中
for(int i=1; i<=n; i++)
{
b[a[i] / size].push_back(a[i]);
}
int p = 0;
for(int i=0; i<n; i++)
{
insort(b[i]); //对每个桶进行插入排序
for(int j=0; j<b[i].size(); j++)
{
a[++p] = b[i][j]; //将每个桶中的元素放回原数组
}
}
}
int main()
{
int x = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
bucketsort();
for(int i=1; i<=n; i++) printf("%d ", a[i]);
return 0;
}
归并排序
原理： 归并排序基于分治思想将数组分段排序后再合并，合并是核心
时间复杂度：
时间复杂度在最优、最坏与平均情况下均为\(O(nlogn)\)，空间复杂度为\(O(n)\)
稳定性： 归并排序是一种稳定排序算法
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
//不断的细分，直到只有一个元素
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
//回溯时进行合并
//将[l, r]这段区间分为[l, mid]和[mid+1, r]两部分，边比较边放入临时数组
int k = 0, i = l, j = mid + 1;
while(i<=mid && j<=r)
{
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
//将前mid前或mid后的剩余元素加入临时数组
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
//将临时数组中的元素，放到原数组，位置是对应的，相当于对这一段进行了排序
for (i=l, j=0; i<=r; i++) q[i] = tmp[j++];
}
前缀和&差分
一维前缀和
主要用于求数列区间和的问题，是一种重要的预处理方式
#include <bits/stdc++.h>
using namespace std;
//a为原数组，s为前缀和
int a[10] = {}, s[10] = {};
int main()
{
for(int i=1; i<=5; i++)
{
scanf("%d", &a[i]);
s[i] = s[i-1] + a[i];
}
int l = 2, r = 4;
//求a数组区间[l,r]的和
int ans = s[r] - s[l-1];
printf("%d", ans);
return 0;
}
二维前缀和
1、计算前缀和
基于容斥原理
给定大小为\(m*n\)的二维数组\(A\),要求出其前缀和\(S\)。那么，\(S\)同样是大小为\(m*n\)的二维数组
且
\(S_{i,j}=\sum_{i'\leqslant i}\sum_{j'\leqslant j}A_{i',j'}\)
如下图：
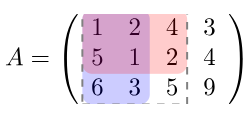
\(S_{i-1,j}\)和\(S_{i,j-1}\)会有\(S_{i-1,j-1}\)的重合，因此，这两部分相加后要减去重合的部分
所以二维前缀和的计算公式为：
\(S_{i,j}=S_{i-1,j}+S_{i,j-1}-S_{i-1,j-1}+A_{i,j}\)
2、计算子矩阵和
在已经预处理出二维前缀和后，要查询左上角为\(（i_1, j_1）\)、右下角为\(（i_2, j_2）\)的子矩阵的和，方式如下：
\(S_{i_2,j_2} - S_{i_1-1,j_2} - S_{i_2,j_1-1} + S_{i_1-1,j_1-1}\)
这可以在\(O(1)\)时间内完成。
在二维的情形，以上算法的时间复杂度可以简单认为是\(O(mn)\)，即与给定数组的大小成线性关系。
例题：[HNOI2003]激光炸弹
https://h.hszxoj.com/d/hztg/p/HNOI2003?tid=67734b28c12f64c045802fa8
#include <bits/stdc++.h>
using namespace std;
/*
二维前缀和
*/
const int maxn = 1e4 + 10;
int n = 0, R = 0;
int a[5010][5010] = {}, s[5010][5010] = {};
int main()
{
int x = 0, y = 0, v = 0;
int ans = 0;
scanf("%d%d", &n, &R);
for(int i=1; i<=n; i++)
{
scanf("%d%d%d", &x, &y, &v);
//让数组下标从1开始，方便计算前缀和
a[x+1][y+1] = v;
}
//求二维前缀和
for(int i=1; i<=5001; i++)
{
for(int j=1; j<=5001; j++)
{
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
}
}
//求边长为R的正方形的和的最大值
for(int i=R; i<=5001; i++)
{
for(int j=R; j<=5001; j++)
{
ans = max(ans, s[i][j] - s[i-R][j] - s[i][j-R] + s[i-R][j-R]);
}
}
printf("%d", ans);
return 0;
}
树上前缀和
一维前缀和还可以推广到有根树（树根为1）的情形。通过预处理前缀和，可以快速求解树上一段路径的权值和。
点权的情形
权值存储在结点处，设结点\(x\)处有权值\(a_x\)，可以通过递推关系
\(S_1=a_1\),\(S_x=S_{\text{fa}(x)}+a_x\)
求出从根结点到结点\(x\)的路径上的节点的权值和，其中，\(fa(x)\)表示\(x\)的父节点。预处理完前缀和后，就可以通过
\(S_x + S_y - S_{\text{lca}(x,y)} - S_{\text{fa}(\text{lca}(x,y))}\)
计算连接节点\(x\)和\(y\)的路径上的节点权值和。其中\(lca(x, y)\)表示节点\(x\)和\(y\)的最近公共祖先
边权的情形
权值储存在边上的情形几乎可以转化为点权的情形。
对于所有非根节点\(x \neq 1\)，记\(edge(x)\)表示连接节点\(x\)和它的父节点\(fa(x)\)的边，那么可以假设边权存储在离根远的节点上，也就是说，节点\(x\)处存储的是边\(edge(x)\)上的边权，根节点处存储的权值是\(0\)。
可以预处理出根节点到节点\(x\)的路径经过的所有边的权值和\(S_x\)，此时，连接节点\(x\)和\(y\)的路径上的节点权值和可以通过
\(S_x + S_y - 2 * S_{\text{lca}(x, y)}\)
进行查询。
注意：与点权的情形不同，所查询的权值和不包括\(lca(x, y)\)处的权值，因为它存储的边权不在所求路径中。
子树和
一般情况下，树上前缀和指的是自上而下计算的前缀和。
这里将自下而上计算的前缀和称为子树和。
以节点\(x\)为根的子树的点权权值和，即相应的子树和，就是
\(T_x = \sum_{y \in \text{desc}(x)} a_x\)
其中，\(desc(x)\)表示\(x\)的所有子孙节点（包括其自身）的集合。
与树上前缀和不同，子树和并不能应用于\(O(1)\)求路径权值和，但是可以用于理解下文的树上差分
差分数组
1、解释
差分是一种和前缀和相对的策略，可以当做是求和的逆运算，定义方式如下：
2、性质
\(a_i\)是\(b_i\)的前缀和，即$$a_j = \sum_{i=1}^{j} b_i$$
3、应用
通过差分数组，可以将原数组的区间修改操作转变为差分数组的单点修改操作，时间复杂度由\(O(n)\)降为\(O(1)\)
4、代码示例
b[1] = a[1];
for(int i=2; i<=n; i++)
{
b[i] = a[i] - a[i-1];
}
浙公网安备 33010602011771号