C++语言基础
编程工具devc++
devc++是一个非常简洁的开发工具,集编辑器和编译器为一体,非常适合初学者使用。
下载地址
https://sourceforge.net/projects/orwelldevcpp/
设置软件为中文
1、点击上方"Tools"->"Environment Options"
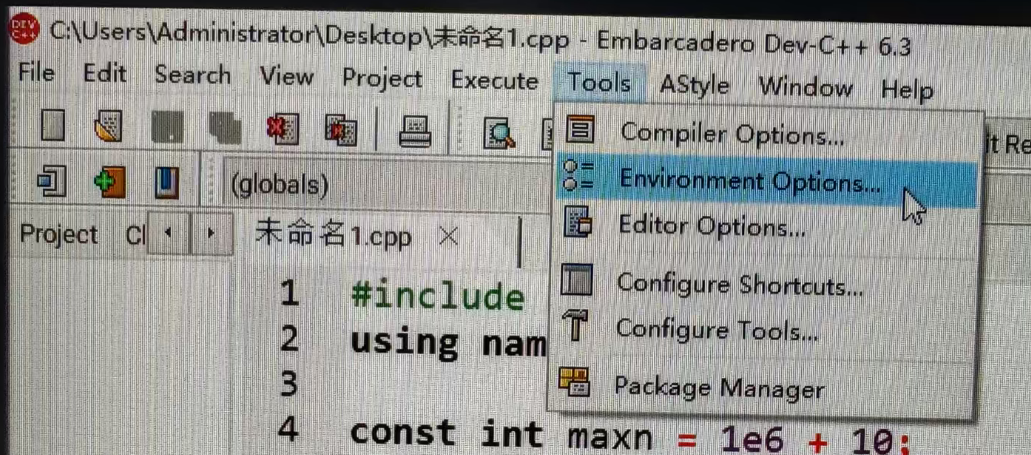
2、找到"Language",选择“简体中文/Chinese”即可
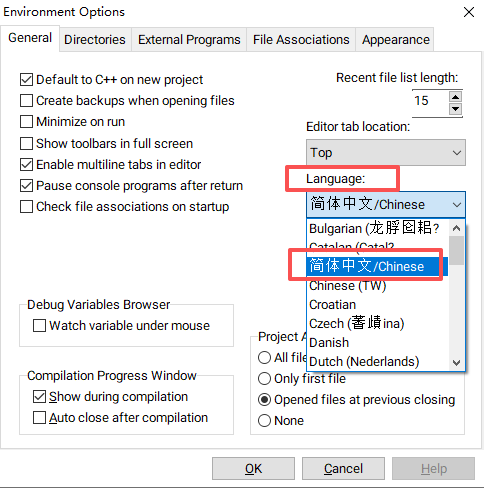
使用方法
1、安装完成后打开软件
2、点击左上角“文件”->“新建”->“源代码”
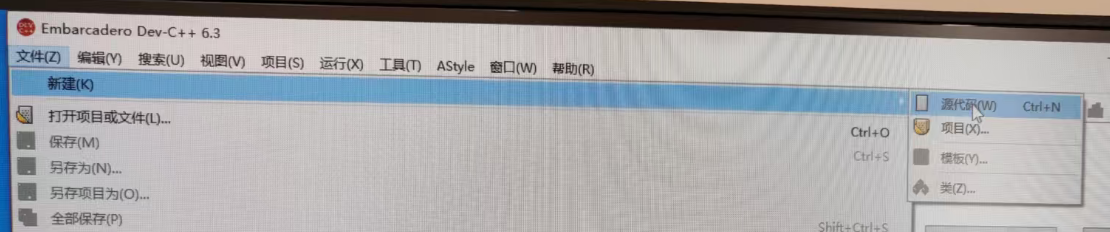
3、点击左上角“文件”->“另存为”,将文件保存到本地
4、打开刚刚保存的文件,开始编写代码
5、编写完代码后,点击“运行”->“编译运行”,即可将代码跑起来
打开调试信息
1、点击上方菜单栏“工具”-“编译选项”
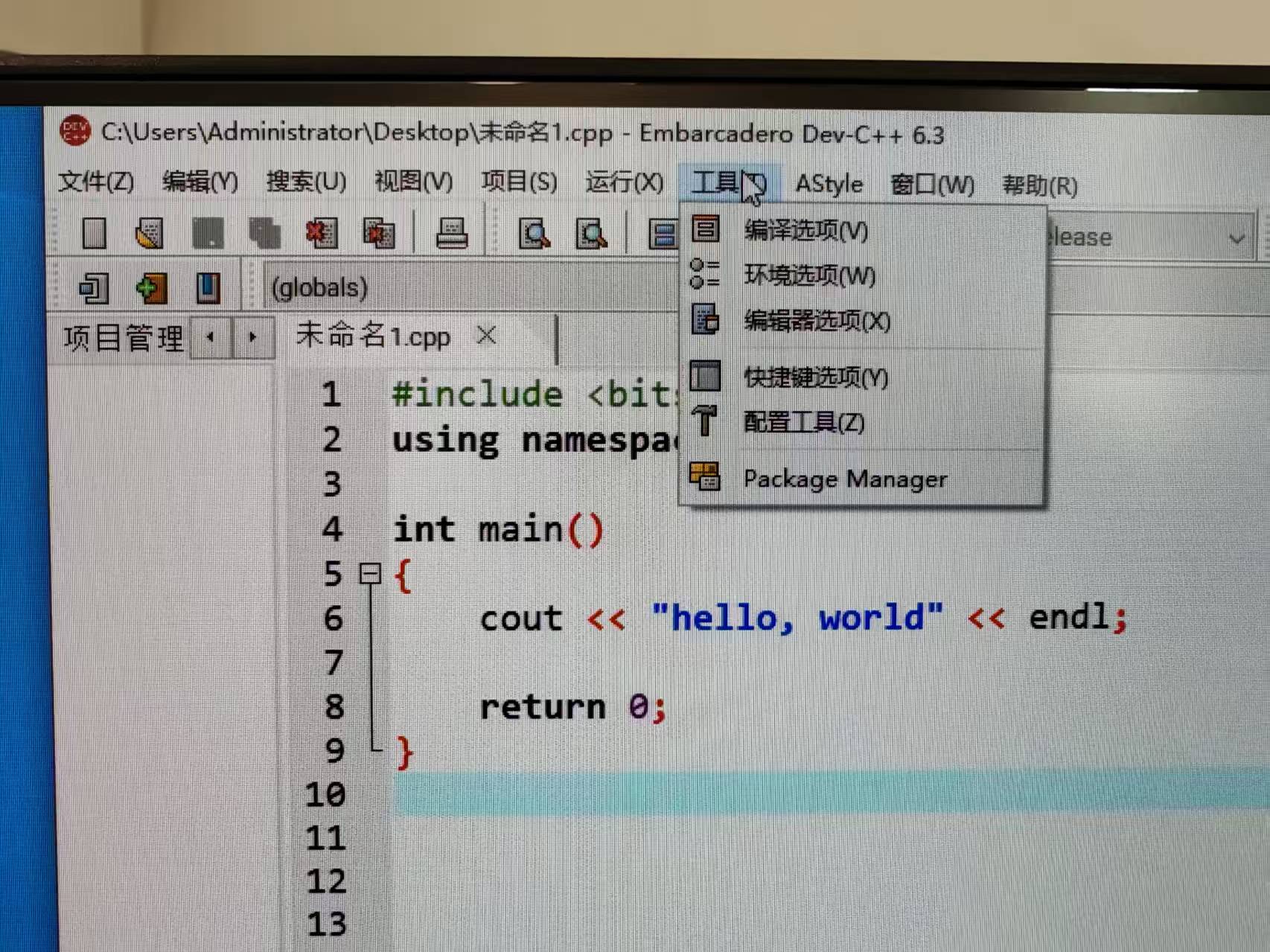
2、选择“代码生成/优化”-“连接器”-“产生调试信息”,改为Yes
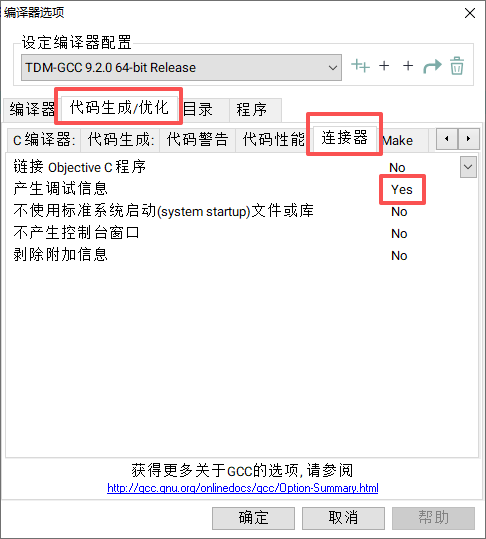
添加编译命令
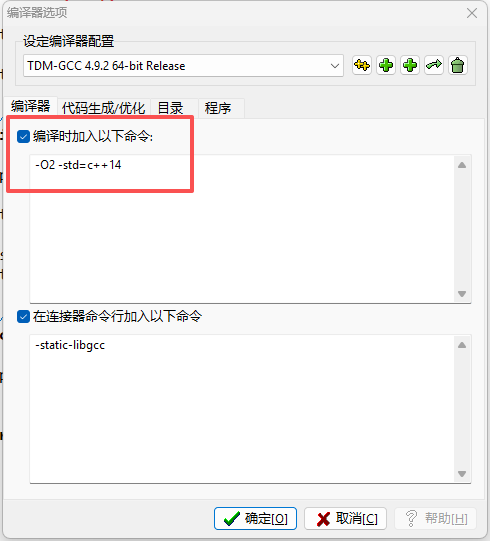
信息学竞赛的编译环境为C++14,开O2,可将命令添加到devc++
命令:-O2 -std=c++14
方法:打开“工具”-“编译选项”,在“编译时加入以下命令”中,添加上述命令
顺序结构
1.1 代码框架
#include <bits/stdc++.h>
using namespace std;
int main()
{
return 0;
}
上述代码为c++程序的主体框架,在写程序前先把这个框架打出来,然后再填充具体内容
#include<bits/stdc++.h>表示包含万能头文件,包含信息奥赛所有功能
using namespace std;声明定义域std
int main() 主函数,c++程序运行时首先进入主函数
return 0;函数的返回值
1.2 程序员的第一段代码“hello, world”
#include <bits/stdc++.h>
using namespace std;
int main()
{
cout << "hello, world" << endl;
return 0;
}
代码解释:
cout为输出功能,上述代码表示输出一个字符串"hello, world",endl表示回车
1.2.1 例题:Hello,World!
#include <bits/stdc++.h> //万能头文件
using namespace std; //包含定义域
int main()
{
cout << "Hello,World!" << endl;
return 0;
}
1.3 变量
在编写程序时,需要输入数据,程序会把这些数据保存到计算机内存当中,而声明一个变量就是在内存中占据一定的空间,对变量的操作就是对内存的操作。
1.3.1 命名规则
①变量名必须以字母或下划线开头,名字中间只能由字母、数字、下划线"_"组成
②变量名在有效范围内必须是唯一的
③变量名不能是关键字
1.3.2 c++中的数据类型
c++中的数据必须有其数据类型,常用的基本数据类型有整形、浮点型、字符型、布尔型。每一种数据类型都有自己的数据范围和在内存中存储大小。
| 类型 | 关键字 | 格式控制符 | 存储(字节) | 范围 |
|---|---|---|---|---|
| 短整型 | short int | %hd | 2 | \(-2^{15}\)~\(2^{15}-1\) |
| 无符号短整型 | unsigned short int | %hu | 2 | \(0\)~\(2^{16}-1\) |
| 整型 | int | %d | 4 | \(-2^{31}\)~\(2^{31}-1\) |
| 无符号整型 | unsigned int | %u | 4 | \(0\)~\(2^{32}-1\) |
| 长整型 | long long | %lld | 8 | \(-2^{63}\)~\(2^{63}-1\) |
| 无符号长整型 | unsigned long long | %llu | 8 | \(0\)~\(2^{64}-1\) |
| 单精度浮点型 | float | %f | 4 | 6~7位有效位数 |
| 双精度浮点型 | double | %lf | 8 | 15~16位有效数 |
| 长双精度浮点型 | long double | %Lf(L大写) | 16 | 18~19位有效数 |
| 字符型 | char | %c | 1 | |
| 布尔型 | bool | 无 | 1 | c++有,c无 |
1.3.3 变量定义
int a; //定义一个整形变量,可用于存储整数
double b;//定义一个双精度浮点型变量,可用于存储小数
char c;//定义一个字符型变量,可用于存储特殊字符
1.4 输入、输出
cin/cout写法
基本写法
int a, b, c, d; //定义4个整型变量
cin >> a; //输入一个变量
cin >> b >> c >> d; //输入多个变量
cout << a; //输出一个变量
cout << b << c << d; //输出多个变量
double d; //定义一个双精度浮点型,用于存储小数
cin >> d; //输入一个小数
cout << d; //输出一个小数
char c; //定义一个字符变量,用于存储特殊字符
cin >> c; //输入一个特殊字符
cout c; //输出一个特殊字符
例题
例题1:A+B
#include <bits/stdc++.h> //万能头文件
using namespace std; //包含定义域
int main()
{
int a, b, c;
cin >> a; //输入a
cin >> b; //输入b
c = a + b; //运算
cout << c; //输出c
return 0;
}
例题2:字符三角形
#include <bits/stdc++.h> //万能头文件
using namespace std; //包含定义域
int main()
{
char c;
cin >> c;
cout << " " << c << " " << endl;
cout << " " << c << c << c << " " << endl;
cout << c << c << c << c << c;
return 0;
}
输入输出流的控制符
| 控制符 | 作 用 |
|---|---|
| dec | 设置数值的基数为10 |
| hex | 设置数值的基数为16 |
| oct | 设置数值的基数为8 |
| setfill(c) | 设置填充字符c,c可以是字符常量或字符变量 |
| setprecision(n) | 设置浮点数的精度为n位。在以一般十进制小数形式输出时,n代表有效数字。在以fixed(固定小数位数)形式和 scientific(指数)形式输出时,n为小数位数 |
| setw(n) | 设置字段宽度为n位 |
| setiosflags( ios::fixed) | 设置浮点数以固定的小数位数显示 |
| setiosftags( ios::scientific) | 设置浮点数以科学记数法(即指数形式)显示 |
| setiosflags( ios::left) | 输出数据左对齐 |
| setiosflags( ios::right) | 输出数据右对齐 |
| setiosflags( ios::skipws) | 忽略前导的空格 |
| setiosflags( ios::uppercase) | 数据以十六进制形式输出时字母以大写表示 |
| setiosflags( ios::lowercase) | 数据以十六进制形式输出时宇母以小写表示 |
| setiosflags(ios::showpos) | 输出正数时给出“+”号 |
使用方法
int a, b, c;
cout << a << " " << b << " " << c; //输出三个变量,用空格隔开
//引号内的字符会原样输出,起到提示作用
cout << "a=" << a << "b=" << b << "c=" << c;
cout << a << " " << b << endl; //endl表示回车
//变量a,b输出最少5个字符,不够左边补空格
cout << setw(5) << a << b << endl;
//输出变量a,保留两位小数
cout << setprecision(2) << fixed << a << endl;
例题
例题1:保留3位小数的浮点数
#include <bits/stdc++.h>
using namespace std;
int main()
{
double a;
cin >> a;
cout << fixed << setprecision(3) << a;
return 0;
}
scanf/printf写法
scanf
说明: 格式化输入函数,用于按指定格式读取数据
基本语法:
scanf("格式字符串", &变量地址1, &变量地址2, ...)
示例:
int a, b;
scanf("%d%d", &a, &b); //读入整型数据
double pi;
scanf("%lf", &pi); //读入双精度浮点型数据
char ch;
scanf("%c", &ch); //读入字符型数据
scanf(" %c", &ch); //%c前加空格,跳过前导空白
char s[100];
scanf("%s", s); //读入字符数组
注意事项:
- 取地址符&:初字符串数组(数组名本身就是地址,无需&)外,其他变量必须使用&传地址
- 空白字符:读\(%c\)时会包括空格/换行,若要跳过前导空白,需要在\(%c\)前加空格
printf
说明: 格式化输出函数,用于将数据按指定格式输出
基本语法:
printf("格式字符串", 变量1, 变量2, ...)
示例:
int a, b;
printf("%d %d", a, b);//输出两个整型数据,以空格隔开
double pi;
printf("%lf", pi); //输出一个双精度浮点型数据
printf("%.2f", pi); //输出一个浮点数,保留两位小数
long double x;
printf("%.2Lf", x); //字母L是大写,专门用于输出long double
char ch;
printf("%c", ch); //输出一个字符
char s[100];
printf("%s", s); //输出字符串s
int a, b;
scanf("%d%d", &a, &b);
printf("%5d%5d", a, b); //整数占5个字符宽度,不足补空格
int a, b;
scanf("%d%d", &a, &b);
printf("%05d%05d", a, b); //整数占5个字符宽度,不足补0
注意事项:
可以通过格式说明符控制精度、宽度等
- 保留\(n\)位小数:%.nf(如%.2f保留2位)
- 指定输出宽度:%5d(整数占5个字符宽度,不足补空格)
- 指定输出宽度:%05d(整数占5个字符宽度,不足补0)
1.5 运算符
1.5.1 赋值运算符 "="
语法:
变量 = 表达式
int a, b;
a = 10; //将a的值设为10
b = a; //将a的值赋给b
a = b = 5; //将a和b的值都设为5
1.5.2 算术运算符
| 运算符 | 描述 |
|---|---|
| + | 把两个操作数相加 |
| - | 从第一个操作数中减去第二个操作数 |
| * | 把两个操作数相乘 |
| / | 分子除以分母 |
| % | 取模运算符,整除后的余数 |
| ++ | 自增运算符,整数值增加 1 |
| -- | 自减运算符,整数值减少 1 |
int a = 8, b = 5, c = 0;
c = a + b; //c为13
c = a - b; //c为3
c = a * b; //c为40
c = a / b; //c为1,此处注意8/5为1.6,但c为int,所以只保留整数部分
c = a % 5; //c为3
a = 8;
a++; //a为9
a = 8;
c = a++; //先执行c=a,再执行a++,故c为8,a为9
a = 8;
c = ++a; //先执行++a, 再执行c=a,故c为9,a为9
a = 8;
a--; //a为7
a = 8;
c = a--; //先执行c=a,再执行a--,故c为8,a为7
a = 8;
c = --a; //先执行--a, 再执行c=a,故c为7,a为7
1.5.3 例题
例题:计算(a+b)×c的值
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 0, b = 0, c = 0, d = 0;
cin >> a >> b >> c;
d = (a + b) * c;
cout << d;
return 0;
}
1.6 常量
常量就是不能被改变的值
1.6.1 类型
常量可以是整形、浮点型、字符型等
10; //单独一个整形,常量
10 = 15; //报错,不能给常量赋值
3.14; //单独一个浮点型,常量
3.14 = 9.3; //报错,不能给常量赋值
'#'; //单独一个字符型,常量
'#' = '*'; //报错,不能给字符常量赋值
1.6.1 自定义常量
1、使用const关键字
const int maxn = 100; //maxn为值为100的常量
maxn = 150; //报错,不能给常量赋值
int n = 0;
n = maxn; //正确,可以把常量的值赋给其他变量
2、使用 #define 宏定义
#define PI 3.14 //PI为值为3.14的常量
PI = 1.23; //报错,不能给常量赋值
double a = 0;
a = PI; //正确,可以把常量的值赋给其他变量
1.7 自动类型转换
1、一个表达式中出现不同类型间的混合运算,较低类型自动向较高类型转换
①整型类别从低到高:
int -> unsigned int -> long -> unsigned long -> long long -> unsigned long long
int a = 10;
long long b = 5;
a + b; //a*b的值类型为long long
②浮点型类别从低到高:
float -> double
float a = 3.14;
double b = 5.2;
a * b; //a*b的值类型为double
③当表达式中有浮点型数据时,所有操作数自动转换为浮点型
int a = 3;
double b = 5.2;
a * b; //a*b的值类型为double
1.8 强制类型转换
形式为:(类型说明符)(表达式)
int a = 12, b = 5;
double c = 0, d = 0;
c = a / b; //c的值为2,因为a和b都为整型,所以a/b也为整型,然后再赋值给c
d = (double)a / b; //d的值为2.4,(double)a强制将a转为浮点型,这样a/b的类型也为浮点型,然后再赋值给d
1.8.1 例题
例题:计算球的体积
#include <bits/stdc++.h>
using namespace std;
const double PI = 3.14;
double v = 0, r = 0;
int main()
{
cin >> r;
v = 4.0 / 3 * PI * r * r * r;
cout << fixed << setprecision(2) << v;
return 0;
}
选择结构
2.1 运算符
2.1.1 关系运算符
下表显示了 C++ 支持的关系运算符。假设变量 A = 10,变量 B=20,则:
| 运算符 | 描述 | 实例 |
|---|---|---|
| == | 检查两个操作数的值是否相等,如果相等则条件为真。 | (A == B) 不为真。 |
| != | 检查两个操作数的值是否相等,如果不相等则条件为真。 | (A != B) 为真。 |
| > | 检查左操作数的值是否大于右操作数的值,如果是则条件为真。 | (A > B) 不为真。 |
| < | 检查左操作数的值是否小于右操作数的值,如果是则条件为真。 | (A < B) 为真。 |
| >= | 检查左操作数的值是否大于或等于右操作数的值,如果是则条件为真。 | (A >= B) 不为真。 |
| <= | 检查左操作数的值是否小于或等于右操作数的值,如果是则条件为真。 | (A <= B) 为真。 |
2.1.2 逻辑运算符
下表显示了 C++ 支持的关系逻辑运算符。假设布尔变量 A = true,布尔变量 B = false,则:
| 运算符 | 描述 | 实例 |
|---|---|---|
| && | 称为逻辑与运算符。如果两个操作数都非零,则条件为真。 | (A && B) 为假。 |
| || | 称为逻辑或运算符。如果两个操作数中有任意一个非零,则条件为真。 | (A || B) 为真。 |
| ! | 称为逻辑非运算符。用来逆转操作数的逻辑状态。如果条件为真则逻辑非运算符将使其为假。 | !(A && B) 为真。 |
ps:若变量为整型,则0为false,非0为true
2.2 if语句
2.1.1 单分支结构
if(条件表达式)
{
语句1;
语句2;
···
}
功能:如果条件表达式的值为真,即条件成立,花括号中的语句将被顺序执行。否则,花括号中的所有语句将被忽略(不被执行),程序将按顺序从整个选择结构之后的下一条语句继续执行。
说明:格式中的“条件表达式”必须用圆括号括起来,执行语句若只有一条,可省略花括号,两条及以上,必须要有花括号
示例代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 15;
//如果a大于10,输出yes
if(a > 10)
{
cout << "yes" << endl;
}
return 0;
}
2.1.2 双分支结构
//条件表达式为true,执行语句1、语句2
//否则执行语句3、语句4
if(条件表达式)
{
语句1;
语句2;
···
}
else
{
语句3;
语句4;
}
功能:如果条件表达式为真(true),执行语句1、语句2,条件表达式为假(false),执行语句3、语句4
示例代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 5;
//如果a大于10,输出yes,否则输出no
if(a > 10)
{
cout << "yes" << endl;
}
else
{
cout << "no" << endl;
}
return 0;
}
2.1.3 多分支结构
if(条件表达1)
{
语句1;
语句2;
···
}
else if(条件表达式2)
{
语句3;
语句4;
}
else if(条件表达式3)
{
语句5;
语句6;
}
else
{
语句7;
语句8;
}
功能:
若条件表达式1为真(true),则执行语句1,语句2。
在条件表达式1为假(false)的情况下,若条件表达式2为真(true),则执行语句3,语句4。
在条件表达式1和2都为假(false)的情况下,若条件表达式3为真(true),则执行语句5,语句6。
在条件表达式1和2和3都为假(false)的情况下,则执行语句7,语句8。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 25;
if(a < 10) //a<10
{
cout << "a" << endl;
}
else if(a > 20) //a>20
{
cout << "b" << endl;
}
else //10<=a && a<=20
{
cout << "c" << endl;
}
return 0;
}
2.1.4 例题
PJ31 判断数正负
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
if(n > 0)
{
cout << "positive" << endl;
}
else if(n < 0)
{
cout << "negative" << endl;
}
else
{
cout << "zero" << endl;
}
return 0;
}
循环结构
for 循环
格式:
for(控制变量初始化;条件表达式;增量表达式)
{
语句1;
语句2;
...
}
说明:
花括号中的内容为循环体,如果循环体中只有一条语句,花括号可以省略
执行过程:
1、执行“控制变量初始化”,使控制变量获得一个初值
2、判断是否满足“条件表达式”,若满足则执行一遍循环体,然后执行第3步;否则结束循环
3、执行增量表达式,计算出控制变量所得到的新值
4、自动跳转到第2步
5、若条件表达式一直为真,则陷入死循环
格式举例:
for(int i=1; i<=100; i++) //控制变量从1变到100,增量为1
for(int i=1; i<=100; i+=5) //控制变量从1变到100,增量为5
for(int i=100; i>=1; i--) //控制变量从100变到1,增量为-1
for(int i=100; i>=1; i-=5) //控制变量从100变到1,增量为-5
例题: PJ52 求平均年龄
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, s = 0, x;
double a;
cin >> n;
for(int i=1; i<=n; i++)
{
cin >> x;
s += x;
}
a = (double)s / n;
cout << fixed << setprecision(2) << a << endl;
return 0;
}
while 循环
格式:
while(条件表达式)
{
语句1;
语句2;
...
}
说明:
花括号内为循环体
执行过程:
1、判断“条件表达式”是否为真,若为真则执行循环体,否则结束循环
2、重复步骤1,直到条件表达式为假
3、若条件表达式一直为真,则陷入死循环
格式举例:
//输出1~10
int i = 1;
while(i <= 10)
{
cout << i << endl;
i++;
}
例题:
求\(s=1+2 +3……+n\),当加到第几项时,\(s\)的值会超过\(1000\)?
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n = 0, s = 0;
while(s <= 1000)
{
n++;
s += n;
}
cout << n; //加到第n项时,s会超过1000
return 0;
}
do...while 循环
格式:
do
{
语句1;
语句2;
...
}while(条件表达式);
说明:
花括号内为循环体
执行过程:
1、先执行一遍循环体
2、判断“条件表达式”是否为真,若为真则执行循环体,否则结束循环
2、重复步骤2,直到条件表达式为假
3、若条件表达式一直为真,则陷入死循环
//只输出输出1
int i = 1;
do
{
cout << i << endl;
i++;
}while(i > 5);
break、continue、return
1、break:终止当前结构,跳出整个循环,执行该循环后面的代码
示例:
for(int i=1; i<=5; i++)
{
if(i == 3) //当i=3时,终止整个for循环
{
break;
}
cout << i << " ";
}
//输出:1 2(i=3时触发break,循环直接结束,不会执行i=3/4/5的迭代)
int i = 1;
while(i <= 5)
{
if(i == 3) break;
cout << i << endl;
i++;
}
//输出1 2(i=3时触发break,循环直接结束)
2、continue:跳过本次循环剩余语句,进入下一次循环
示例:
for(int i=1; i<=5; i++)
{
if(i == 3) //当i=3时,跳过本次循环剩余语句,直接进入下一次循环
{
continue;
}
cout << i << " ";
}
//输出:1 2 4 5(i=3时触发continue,跳过了cout,直接执行i++进入下一次循环)
int i = 1;
while(i <= 5)
{
if(i == 3)
{
i++;
continue;
}
cout << i << endl;
i++;
}
//输出:1 2 4 5(i=3时触发continue,跳过了cout)
3、return:用于退出函数,具体作用见“函数”章节
在main中return 0;就是退出主函数,即退出整个程序
#include <bits/stdc++.h>
using namespace std;
int main()
{
//该段代码只输出1 2
//在i=3的时候,执行return 0,程序就结束了
for(int i=1; i<=5; i++)
{
if(i == 3) return 0;
cout << i << " ";
}
cout << "hello world" << endl;
return 0;
}
循环嵌套
顾名思义,在循环中嵌套循环
例题:
PJ77 【循环结构】阶乘和
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n = 0;
long long sum = 0, a = 0;
cin >> n;
for(int i=1; i<=n; i++)
{
a = 1;
for(int j=1; j<=i; j++)
{
a *= j;
}
sum += a;
}
cout << sum;
return 0;
}
数组
数组是存放相同类型对象的容器,数组中存放的对象没有名字,而是要通过其所在的下标访问。
- 数组的大小是固定的,不能随便改变数组的长度
- 一个数组的所有元素在内存中的存储位置是连续的
一维数组
数组的定义
格式: 数据类型 数组名[常量表达式]
例子:
int a[10]; //定义能存储10个整型变量的数组,下标是:0~9
char c[100]; //定义能存储100个字符变量的数组,下标是:0~99
double f[5]; //定义能存储5个双精度实数变量的数组,下标是:0~4
说明:
1、数组名的命名规则与变量名的命名规则一致
2、常量表达式表示数组元素的个数。可以是常量和符号常量,不能是变量
3、数组的长度必须是整数
错误示例:
int n;
cin >> n;
int a[n]; //不能用变量n定义数组
数组的初始化
数组的初始化可以在定义时一并完成,有多种形式
1、顺序指定全部元素的初始值
int a[5] = {1, 2, 3, 4, 5};
2、顺序指定部分元素的初始值
int a[10] = {0, 1, 2, 3, 4}; //该方法仅对数组的前5个元素依次进行初始化,其余值为0
3、对数组元素全部初始化为0,可以简写为:{}或{0}
int a[5] = {};
4、初始化时不指定数组元素的个数(不常用)
int a[] = {1, 2, 3}; //该方法会定义一个长度为3的数组,每个元素初始值依次为1,2,3
注意: 初始化时,{}里面的元素个数不能超过数组的大小
数组元素的引用
格式: 数组名[整型表达式]
规定:
1、下标可以是任意值为整型的表达式,该表达式里可以包含变量和函数调用。
2、下标的范围是0到数组的最大长度减1,引用时,下标值应在数组合法的下标值范围内。例如定义数组int a[3],则元素分别为a[0],a[1],a[2]
3、C语言只能逐个引用数组元素,而不能一次引用整个数组
4、数组元素可以像同类型的普通变量那样使用,对其进行赋值和运算的操作,和普通变量完全相同。例如:a[5]=34,实现了给a[5]赋值为34
例如:
a[5] //引用a数组下标为5的元素
a[i+1] //先计算表达式i+1的值,再引用相应值作为下标的元素
a[++j] //先计算表达式++j的值,再引用相应值作为下标的元素
数组的输入和输出
- C语言规定,对数组的使用只能逐个引用数组元素,不能一次引用整个数组。同样,对数组的输入输出也是一次对每个元素进行的,不可整体输入输出。
- 数组往往和循环一起结合使用,通常用循环里面的控制变量来作为数组的下标,对数组的每个元素进行引用
例如:输入\(n\)个整数,并将他们输出
int n, a[20];
cin >> n;
for(int i=0; i<n; i++)
{
cin >> a[i];
}
for(int i=0; i<n; i++)
{
cout << a[i] << " ";
}
例题
PJ86 与指定数字相同的数的个数
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m, a[110], ans = 0;
cin >> n;
for(int i=1; i<=n; i++)
{
cin >> a[i];
}
cin >> m;
for(int i=1; i<=n; i++)
{
if(a[i] == m) ans++;
}
cout << ans;
return 0;
}
二维数组
形象的来说,一维数组是一条线,二维数组则是有很多条线组成的面。
注意:在内存存储中,一维数组和二维数组的地址都是连续的
二维数组的定义
格式: 数据类型 数组名[常量表达式1][常量表达式2]
int a[10][5]; //定义一个10行5列的存储整型变量的二维数组
double b[20][9]; //定义一个20行9列的存储双精度浮点型变量的二维数组
char c[100][120]; //定义一个100行120列的字符变量二维数组
一维数组和二维数组直观上的区别:
一维数组:

二维数组:

二维数组的初始化
数组的初始化可以在定义时一并完成,有多种形式:
1、顺序指定全部元素的初始值(每一行数据单独写在一个花括号里,中间以逗号隔开)
int a[3][2] = {{1, 2}, {3, 4}, {5, 6}};
2、顺序指定部分元素的初始值
int x[10][2] = {{0, 1}, {2}, {3, 4}}; //该方法仅对数组对应位置的元素依次进行初始化,其余值为0
3、对数组元素全部初始化为0,可以简写为:{}或{0}
int a[5][3] = {}; //将数组a的15个元素都初始化为0
4、初始化时不指定行数,但必须指定列数
int a[][2] = {{1, 2}, {3, 4}}; //该方法会定义一个2行2列的数组,每个元素的初始值依次为1,2,3,4
注意: 初始化时,{}里面的元素个数不能超过数组的大小
二维数组的引用
格式: 数组名[行下标][列下标]
规定:
1、与一维数组一致
2、定义数组int a[3][3],则元素分别为:
a[0][0], a[0][1], a[0][2]
a[1][0], a[1][1], a[1][2]
a[2][0], a[2][1], a[2][2]
例如:
a[5][10]; //引用下标为5和10的元素
a[i+1][j-1]; //先计算i+1和j-1再引用
a[++j]; //先计算++j,再引用
二维数组的输入和输出
例如: 输入n行m列的整数,并将他们输出
int n, m, a[20][20];
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
cin >> a[i][j];
}
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=m; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
例题
PJ95 杨辉三角
#include <bits/stdc++.h>
using namespace std;
/*
杨辉三角转化为二维数组可这样直观表示
0 0 0 0 0 0 0
0 1 0 0 0 0 0
0 1 1 0 0 0 0
0 1 2 1 0 0 0
0 1 3 3 1 0 0
0 1 4 6 4 1 0
...
找规律:
①a[1][1]固定为1
②其他位置的值可认为是其正上方的值加其左上方的值
即a[i][j] = a[i-1][j] + a[i-1][j-1]
③杨辉三角中,第i行共有i个数
*/
int main()
{
int n;
//针对输入不确定个数的值,这样处理
//cin >> n表示读入一个数,成功返回true,失败返回false
//while(cin >> n)表示一直读取数据,直到读取失败(即读完)
while(cin >> n)
{
int a[40][40] = {};
a[1][1] = 1;
for(int i=2; i<=n; i++)
{
for(int j=1; j<=i; j++)
{
a[i][j] = a[i-1][j] + a[i-1][j-1];
}
}
//格式化输出
for(int i=1; i<=n; i++)
{
for(int j=1; j<=i; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
return 0;
}
字符数组
定义
格式:char 数组名[常量表达式]
例如:char sz[100];
初始化
1、用字符初始化
char sz[6] = {'a', 'b', 'c', 'd', 'e'};
从首元素开始赋值,剩余元素默认为空字符(也叫结束符,用'\0'表示,其ASCII码为0)
2、用字符串常量初始化
char sz1[5] = {"abcd"};
char sz2[5] = "abcd";
字符串常量的长度不能超过数组的长度,其中的每个字符依次为数组的每个元素进行初始化,剩余的元素用空字符'\0'补全
输入输出
输入
1、cin语句
格式:cin >> 字符数组名,读入字符串,遇空格、回车结束。
char s[100];
cin >> s;
//输入:abc def
//输出:abc
//因为cin遇到空格即结束
2、scanf语句
格式:
scanf("%s", 字符数组名称),读取一个字符串
scanf("%s%s%s", 字符数组名称1, 字符数组名称2, 字符数组名称3),读取多个字符串
char s1[100], s2[100], s3[100];
scanf("%s%s%s", s1, s2, s3);
//输入 Let us go
//s1为"Let",s2为"us",s3为"go"
3、cin.getline()
格式:
cin.getline(字符数组名,字符个数)
cin.getline(字符数组名,字符个数,结束符)
此函数会一次读取多个字符(包括空格、tab),直到读满 “字符个数”-1 个字符。
若不指定结束符,则默认以回车或EOF作为结束符。
若指定结束符,则以结束符或EOF作为结束符(可以读入回车)。
char s[100];
cin.getline(s, 3); //读取前2个字符,若输入少于2,则遇到回车或EOF截止
//输入abcde
//s为ab
//输入a
//s为a
char s[100];
cin.getline(s, 3, 'b'); //读取前2个字符,若存在'b'则读到'b'截止,否则读满2个字符或遇到EOF为止
//输入abcde
//s为a
//输入a\nb \n为回车
//输出a\n
输出
1、cout语句
格式:cout << 字符串名
char s[100];
cout << s;
2、printf语句
格式:printf("%s", 字符数组名)
说明:输出内容遇到结束符'\0'才会结束
char s[100];
printf("%s", s);
3、puts函数
格式:puts(字符数组名);
说明:
①puts函数输出一个字符串和一个换行符
②printf("%s\n", s)和puts(s)是等价的
char s[100];
puts(s);
字符串处理函数
1、strcat(dst, src),将src连接到dst后面
char s1[100] = "hello", s2[100] = "world";
strcat(s1, s2);
cout << s1; //输出helloworld
2、strncat(dst, src, num),将src的前num个字符连接到dst的后面
char s1[100] = "hello", s2[100] = "world";
strncat(s1, s2, 3);
cout << s1; //输出hellowor
3、strcpy(dst, src),将src复制到dst
char s1[100] = "hello", s2[100] = "world";
strcpy(s1, s2);
cout << s1; //输出world
4、strncpy(dst, src, num),将src的前num个字符复制到dst
注意:该函数只单纯复制字符,不会在后面添加终止符
char s1[100] = "hello", s2[100] = "world";
strncpy(s1, s2, 3);
cout << s1; //输出worlo
5、int strcmp(str1, str2),比较字符串str1和str2的大小
说明:
从两个字符串的第一个字符开始比较其字符的ASCII,如果同一位置字符相同,接着比较后面的字符,直到不同为止
str1<str2:返回负数
str1=str2:返回0
str1>str2:返回正数
int a = 0, b = 0, c = 0;
a = strcmp("abc", "def");
b = strcmp("abc", "abc");
c = strcmp("abc", "ab");
cout << a << endl; //a<0
cout << b << endl; //b=0
cout << c << endl; //c>0
6、int strncmp(str1, str2, num),比较字符串str1和str2前num个字符的大小
int a = 0, b = 0, c = 0;
char s1[100] = "abc", s2[100] = "abcdef";
a = strncmp(s1, s2, 5);
b = strncmp(s1, s2, 3);
c = strncmp("abcdef", "abc", 5);
cout << a << endl; //a<0
cout << b << endl; //b=0
cout << c << endl; //c>0
7、strlen(str),返回字符数组的长度,不包括终止符
char s[100] = "abc";
int len = 0;
len = strlen(s);
cout << len; //len=3
8、char *strstr(str1, str2),判断str2是否是str1的子串
说明:
①如果str2是str1的一个子串,返回一个指向str2在str1中首次出现的位置
②如果str2不是str1的一个子串,返回空指针NULL
char s[100] = "abcdef";
if(strstr(s, "cd") != NULL)
{
cout << "yes";
}
else
{
cout << "no";
}
char s[100] = "abcdef";
int pos = 0;
char *p = strstr(s, "cd");
if(p != NULL)
{
pos = p - s;
cout << pos; //输出2,即cd在abcdef中首次出现的位置,下标从0开始
}
例题
ybt1138 将字符串中的小写字母转换成大写字母
#include <bits/stdc++.h>
using namespace std;
char s[110];
int main()
{
int len = 0;
cin.getline(s, 110); //输入字符串包含空格
len = strlen(s);
for(int i=0; i<len; i++)
{
if(s[i] >= 'a' && s[i] <= 'z') //小写字母
{
printf("%c", s[i] - 'a' + 'A'); //转大写
}
else
{
printf("%c", s[i]);
}
}
return 0;
}
附 ASCII表

函数
函数的概念与意义
在\(c++\)中,函数 是一段封装了特定功能的可重用的代码块,通过函数名被调用。
核心价值:
- 代码复用:避免重复编写相同逻辑,降低冗余
- 模块化:将复杂问题拆解为多个小功能,便于维护和调试
- 可读性:通过函数名直观理解代码功能,提升程序清晰度
例如: 计算两个数的和可以封装为\(add\)函数,后续无需重复编写加法逻辑,直接调用即可。
函数的定义与声明
函数的定义:实现功能的具体代码
函数定义的完整结构如下:
返回值类型 函数名(参数列表)
{
//函数体:实现功能的语句
return 返回值; //若返回值类型为void,可省略return
}
说明:
- 返回值类型:函数执行后返回的数据类型(如:int/double/void等)。void表示无返回值
- 函数名:遵循标识符命名规则(字母、数字、下划线,首字符非数字)
- 参数列表:函数接收的输入数据,格式为"类型 参数名",多个参数用逗号分隔(无参数时写())
- 函数体:用{}包裹的语句块,实现具体功能
- return 语句:将结果返回给调用者,若返回值类型为void,可省略(或仅写return;),只要执行到return,则代表该函数结束
示例:
//1、无参数、无返回值(void)
void p()
{
printf("hello world");
}
//2、有参数、有返回值(int)
int myadd(int a, int b)
{
int s = a + b;
return s;
}
//3、多参数、返回值为double
double ave(double a, double b)
{
return (a + b) / 2;
}
函数声明:告诉编译器函数的存在
函数定义在调用位置,之前:不用声明;之后:需要声明
格式: 仅保留函数结构,省略函数体,以分号结尾
即:返回值类型 函数名(参数列表);
示例:
#include <bits/stdc++.h>
using namespace std;
//函数声明(告知编译器:存在一个add函数)
int myadd(int a, int b);
int main()
{
int x = 1, y = 1, z = 0;
z = myadd(x, y); //调用add函数
printf("%d", z); //输出2
return 0;
}
//函数定义
int myadd(int a, int b)
{
return a + b;
}
说明:
- 函数声明时参数名可省略(仅需类型),如int add(int, int);,但保留参数名更容易理解
- 声明需与定义的“返回值类型、函数名、参数列表”完全一致(否则编译错误)
函数的调用与参数传递
函数调用是执行函数功能的过程,需传递实际参数(实参)给形式参数(形参)
函数调用的格式
格式:
- 函数名(实参列表); //无返回值时
- 返回值类型 变量 = 函数名(实参列表) //有返回值时
示例:
#include <bits/stdc++.h>
using namespace std;
void p()
{
printf("hello world");
}
int myadd(int a, int b)
{
int s = a + b;
return s;
}
int main()
{
int x = 1, y = 1, z = 0;
z = myadd(x, y); //调用有参函数,接收返回值
printf("%d\n", z);
p(); //调用无参函数
return 0;
}
实参与形参的关系
- 形参:函数定义时的参数(如add(int a, int b)中的a.b),仅在函数体内有效(局部变量)
- 实参:调用函数时传递的具体值(如add(x, y)中的x.y),可以是常量、变量或表达式
- 传递规则:实参与形参的类型、个数、顺序必须一一对应,否则编译错误
参数传递方式:值传递(默认)
c++默认采用值传递:将实参的“值副本”传递给形参,函数内修改形参不会影响实参。
示例: 值传递的特性
#include <bits/stdc++.h>
using namespace std;
void myswap(int x, int y)
{
int t = 0;
t = x;
x = y;
y = t;
printf("x=%d, y=%d\n", x, y);
}
int main()
{
int a = 3, b = 5;
myswap(a, b);
printf("a=%d, b=%d\n", a, b);
return 0;
}
结论: 值传递中,形参与实参是独立变量,修改形参不影响实参
局部变量与全局变量
局部变量
定义位置: 在函数内部、代码块(如\(if/for/while\)的\({}\)内)或函数参数列表中定义的变量。
作用域: 仅在定义他的函数或代码块内部有效,出了这个范围就无法访问。
生命周期: 从进入作用域(如函数被调用、代码块开始执行)时创建,离开作用域(如函数执行结束、代码块执行完毕)时自动销毁。
初始化: 若未手动初始化,局部变量的值是未定义的(即随机值),使用时可能导致程序异常。
#include <bits/stdc++.h>
using namespace std;
void test()
{
int a = 10; //局部变量(函数内部)
if(a > 5)
{
int b = 20; //局部变量(if代码块内部)
printf("b = %d\n", b); //有效:在if块内
}
//printf("b = %d\n", b); //错误:出了if块,b已销毁
printf("a = %d\n", a); //有效:在test函数内
}
int main()
{
test();
//printf("a = %d\n", a); //错误:a是test函数的局部变量,main中不可访问
return 0;
}
全局变量
定义位置: 在所有函数和代码块之外(通常在文件顶部)定义的变量。
作用域: 从定义位置开始,整个程序文件内有效。
生命周期: 从程序启动(main函数执行前)创建,直到程序结束(main函数执行完毕)才销毁。
初始化: 若未手动初始化,会被编译器默认初始化为0.
#include <bits/stdc++.h>
using namespace std;
int a = 100; //全局变量(函数外部)
void func1()
{
printf("func1: a=%d\n", a); //有效
}
void func2()
{
a = 200; //修改全部变量
printf("func2: a=%d\n", a);
}
int main()
{
func1(); //输出:100
func2(); //输出:200
printf("main: a=%d\n", a); //输出:200(已被func2修改)
return 0;
}
屏蔽规则
当局部变量与全局变量同名时,局部变量会屏蔽全局变量(优先访问局部变量)
ps:自己写代码时应避免同名
#include <bits/stdc++.h>
using namespace std;
int a = 10; //全局变量
int main()
{
a = 20; //局部变量(与全局变量同名)
printf("a = %d\n", a); //输出20(局部变量屏蔽全局变量)
return 0;
}
例题
PJ132 求阶乘和
#include <bits/stdc++.h>
using namespace std;
long long jc(int k)
{
long long ret = 1;
for(int i=1; i<=k; i++)
{
ret *= i;
}
return ret;
}
int main()
{
int n = 0;
long long ans = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
ans += jc(i);
}
printf("%lld", ans);
return 0;
}
递归
定义:
在数学和计算机科学中是指在函数的定义中使用函数自身的方法,在计算机科学中还额外指一种通过重复将问题分解为同类的子问题而解决问题的方法。
简而言之:函数直接或间接的调用自身,称为递归。适用于解决“可拆解为同类子问题”的场景。
递归的两个必要条件:
1、终止条件: 当满足某条件时停止递归(避免无限循环)
2、递归关系: 将原问题拆解为规模更小的子问题
递归的调用过程:
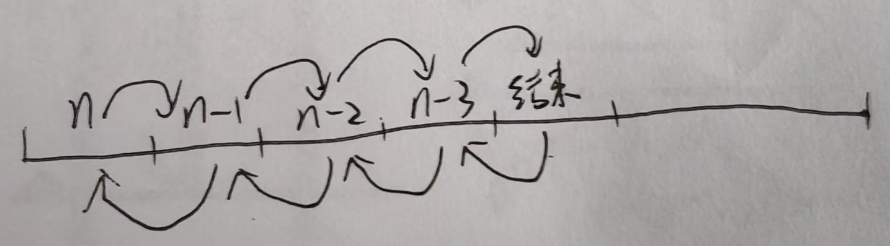
1、当参数为\(n\)时,调用一次函数,占用一段内存,然后执行参数\(n-1\),再调用一次函数,占用一段内存,直到参数到达结束条件。
2、当最后一次函数执行完毕后,将所需要的结果返回上一层函数,直到返回\(n\)时,得到最终结果,结束递归。
为什么要写递归:
1、结构清晰,可读性强
2、练习分析问题的结构。当发现问题可以被分解成相同结构的小问题时,递归写多了就能敏锐发现这个特点,进而高效解决问题
缺点:
在程序执行中,递归是利用堆栈来实现的。每当进入一个函数调用,栈就会增加一层栈帧,每次函数返回,栈就会减少一层栈帧。
而栈不是无限大的,当递归层数过多时,就会造成栈溢出的后果。
写递归的要点:
明白一个函数的作用并相信它能完成这个任务,千万不要跳进这个函数里面企图探究更多细节。
否则就会陷入无穷的细节无法自拔,人脑能压几个栈啊。
例题:
PJ189 【递归】求f(x,n)
#include<bits/stdc++.h>
using namespace std;
int n = 0;
double x = 0;
double f(double x, int n)
{
if(n == 1) return sqrt(1+x);
return sqrt(n+f(x, n-1));
}
int main()
{
scanf("%lf%d", &x, &n);
printf("%.2lf\n", f(x, n));
return 0;
}
结构体
概念
概念: 结构体是一种用户自定义的数据类型,用于将多个不同类型的数据(成员)组合成一个整体,以实现一个“实体”的属性。
例如:
描述一个“学生”,需要包含姓名(字符数组)、年龄(整数)、成绩(浮点数)等信息。
核心价值:
将关联的数据“打包”,使代码更符合现实世界的实体描述,提升可读性和维护性。
定义与初始化
结构体的定义
格式:
struct 结构体名
{
成员类型1 成员名1; //成员可以是基本类型、数组、指针、其他结构体等
成员类型2 成员名2;
//... 更多成员
}; //注意末尾的分号
说明:
- 结构体名:遵循标识符命名规则
- 成员:结构体包含的“属性”,每个成员有自己的类型和名称
- 结构体定义本身不分配内存,仅声明一种新的数据类型
示例:
struct Student
{
int id; //学号(整数)
char name[20]; //姓名(字符数组)
double score; //成绩(浮点数)
};
结构体变量的定义与初始化
定义
1、先定义结构体,再定义变量
struct Student
{
int id; //学号(整数)
char name[20]; //姓名(字符数组)
double score; //成绩(浮点数)
};
Student stu1, stu2; //定义两个结构体变量
2、定义结构体的同时定义变量
struct Student
{
int id; //学号(整数)
char name[20]; //姓名(字符数组)
double score; //成绩(浮点数)
}stu1, stu2; //定义两个结构体变量
初始化
定义时初始化
struct Student
{
int id; //学号(整数)
char name[20]; //姓名(字符数组)
double score; //成绩(浮点数)
};
Student stu1 = {1, "zhangsan", 80.5}; //依次为成员赋值
Student stu2 = {}; //初始化所有成员为0
成员访问
用点运算符(.)
#include <bits/stdc++.h>
using namespace std;
struct Student
{
int id; //学号(整数)
char name[20]; //姓名(字符数组)
double score; //成绩(浮点数)
};
Student stu1 = {1, "zhangsan", 80.5}; //依次为成员赋值
Student stu2 = {}; //初始化所有成员为0
int main()
{
//读取值
printf("%d\n%s\n%lf\n", stu1.id, stu1.name, stu1.score);
//赋值
stu2.id = 2;
strcpy(stu2.name, "lisi");
stu2.score = 100;
printf("%d\n%s\n%lf\n", stu2.id, stu2.name, stu2.score);
//相同类型的变量可以直接赋值
stu2 = stu1;
printf("%d\n%s\n%lf\n", stu2.id, stu2.name, stu2.score);
return 0;
}
内存分配机制
注意: 定义一个结构体类型时不分配内存,只有定义结构体变量时才分配内存
原则: 结构体的总大小为其最宽基本类型成员大小的整数倍。
struct Student
{
char a;
int b;
char c;
}stu;
//stu在内存中占12个字节
//int b占4个字节,所以char a后面会自动补3个字节,char c后面也会自动补3个字节
struct Student
{
char a;
char c;
int b;
}stu;
//stu在内存中占8个字节
//int b占4个字节,char a和char c各占一个字节,后面自动补充2个字节
提示:
在竞赛阶段,为了节约内存,在组织数据结构的数据成员的时候,可以将相同类型的成员放在一起,这样就减少了编译器为了对齐而添加的填充字符。
补充:
sizeof 是c++中的一个运算符(非函数),用于计算变量、数据类型在内存中所占的字节数
示例:
#include <bits/stdc++.h>
using namespace std;
struct Student
{
char a;
int b;
char c;
}stu;
int s[10];
int main()
{
int x = sizeof(stu); //计算stu所占内存
int y = sizeof(int); //计算int类型所占内存
int z = sizeof(s); //计算数组s所占内存
//x=12,y=4,z=40
printf("x=%d,y=%d,z=%d\n", x, y, z);
return 0;
}
运算符重载
结构体是构造类型,无法直接进行逻辑运算、四则运算等,但我们可以对相应的运算符进行重载。
1、作为成员变量重载
格式:
bool operator 运算符(const 结构体类型名 &参数) const
{
//条件表达式
}
说明:
1、operator为关键字
2、第一个const表示形参为只读
3、第二个const表示不允许修改成员变量,固定格式
示例:
#include <bits/stdc++.h>
using namespace std;
struct Student
{
int id; //学号(整数)
char name[20]; //姓名(字符数组)
double score; //成绩(浮点数)
//重载运算符<
bool operator < (const Student &s) const
{
//id表示本身的成员变量
//s.id表示参数的成员变量
return id < s.id;
}
}stu1, stu2;
int main()
{
stu1.id = 1;
strcpy(stu1.name, "zhangsan");
stu1.score = 100;
stu2.id = 2;
strcpy(stu2.name, "lisi");
stu2.score = 80;
//结果输出yes
if(stu1 < stu2) printf("yes");
else printf("no");
return 0;
}
2、全局重载
格式:
bool operator 运算符 (const 结构体类型名 &参数1, const 结构体类型名 &参数2)
{
//条件表达式
}
示例:
#include <bits/stdc++.h>
using namespace std;
struct Student
{
int id; //学号(整数)
char name[20]; //姓名(字符数组)
double score; //成绩(浮点数)
}stu1, stu2;
bool operator < (const Student &a, const Student &b)
{
return a.id < b.id;
}
int main()
{
stu1.id = 1;
strcpy(stu1.name, "zhangsan");
stu1.score = 100;
stu2.id = 2;
strcpy(stu2.name, "lisi");
stu2.score = 80;
//结果输出yes
if(stu1 < stu2) printf("yes");
else printf("no");
return 0;
}
文件操作
文件是根据特定的目的而收集在一起的有关数据的集合。C/C++把每一个文件都看成是一个有序的字节流,每个文件都是以文件结束标志(EOF)结束。
freopen(函数)
函数用于将制定输入输出流以指定方式重定向到文件,包含于头文件stdio.h(cstdio)中,该函数可以在不改变代码原貌的情况下改变输入输出环境,但使用时应当保证流是可靠的。
命令格式:
FILE* freopen(const char* filename, const char* mode, FILE* stream);
参数说明:
1、filename:要打开的文件名
2、mode:文件打开的模式,表示文件访问的权限
3、stream:文件指针,通常使用标准文件流(stdin/stdout)或标准错误输出流(stderr)
4、返回值:文件指针,指向被打开文件
文件打开格式:
信息奥赛中常用的就两种:
1、r:以只读方式打开文件,文件必须存在,只允许读入数据
2、w:以只写方式打开文件,文件不存在会新建文件,否则清空内容,只允许写入数据
使用方法:
1、读入文件内容:
//data.in 就是读取的文件名,要和可执行文件放在同一目录下
freopen("data.in", "r", stdin);
2、输出到文件
//data.out就是输出文件的文件名,和可执行文件在同一目录下
freopen("data.out", "w", stdout);
3、关闭标准输入/输出流
fclose(stdin);
fclose(stdout);
注:
printf/scanf/cin/cout等函数默认使用stdin/stdout,将stdin/stdout重定向后,这些函数将输入/输出到被定向的文件
示例代码
#include <bits/stdc++.h>
using namespace std;
int main()
{
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
/*
中间的代码不需要改变,直接使用 cin 和 cout 即可
*/
fclose(stdin);
fclose(stdout);
return 0;
}
标准模板库(STL)
C++标准模板库(Standard Template Library,简称 STL)是\(C++\)标准库的核心组成部分,它提供了一套通用的、可复用的模板类和函数。
sort函数
STL提供的\(sort\)函数是基于模板实现的高效排序工具,支持多种类型,且可自定义排序规则。
格式:
\(sort\)(起始位置,起始位置+长度)
\(sort\)(起始位置,起始位置+长度,自定义比较规则)
说明:
①自定义比较规则,可省略,如果省略,默认按升序排列
②\(sort\)默认通过元素的\(<\)(小于号)运算符比较大小,支持任意可比较的数据类型(如:\(int\)、\(double\)等)
默认升序排序
#include <bits/stdc++.h>
using namespace std;
int main()
{
//对3, 2, 9, 1, 5进行升序输出
int a[10] = {0, 3, 2, 9, 1, 5};
//a+1为起始位置,a+1+5为起始位置+长度
//没有自定义比较规则,所以默认升序
sort(a+1, a+1+5);
//输出结果为:1 2 3 5 9
for(int i=1; i<=5; i++)
{
printf("%d ", a[i]);
}
return 0;
}
自定义排序规则
需要自定义自定义比较规则(\(cmp\)),\(cmp\)函数返回值为\(bool\),表示“是否让第一个参数排在第二个参数前面”
1、对整数数组排序
#include <bits/stdc++.h>
using namespace std;
bool cmp(int x, int y)
{
return x > y;
}
int main()
{
//对3, 2, 9, 1, 5进行降序输出
int a[10] = {0, 3, 2, 9, 1, 5};
//cmp为自定义比较规则
sort(a+1, a+1+5, cmp);
//输出结果为:9 5 3 2 1
for(int i=1; i<=5; i++)
{
printf("%d ", a[i]);
}
return 0;
}
2、对结构体排序
2.1 对结构体重载\(<\)(小于号)运算符
#include <bits/stdc++.h>
using namespace std;
struct node
{
int id; //学号
int score; //分数
bool operator < (const node &nd) const
{
return id < nd.id;
}
}a[10];
int main()
{
a[1].id = 1000;
a[1].score = 90;
a[2].id = 3239;
a[2].score = 88;
a[3].id = 2390;
a[3].score = 95;
a[4].id = 7231;
a[4].score = 84;
a[5].id = 1005;
a[5].score = 95;
sort(a+1, a+1+5);
for(int i=1; i<=5; i++)
{
printf("%d %d\n", a[i].id, a[i].score);
}
//输出结果:
//1005 95
//2390 95
//1000 90
//3239 88
//7231 84
return 0;
}
2.2 自定义自定义比较规则(\(cmp\))
#include <bits/stdc++.h>
using namespace std;
struct node
{
int id; //学号
int score; //分数
}a[10];
//自定义规则,按分数从高到低
//若分数相同,则按学号从低到高
bool cmp(node nd1, node nd2)
{
if(nd1.score == nd2.score) return nd1.id < nd2.id;
return nd1.score > nd2.score;
}
int main()
{
a[1].id = 1000;
a[1].score = 90;
a[2].id = 3239;
a[2].score = 88;
a[3].id = 2390;
a[3].score = 95;
a[4].id = 7231;
a[4].score = 84;
a[5].id = 1005;
a[5].score = 95;
sort(a+1, a+1+5, cmp);
for(int i=1; i<=5; i++)
{
printf("%d %d\n", a[i].id, a[i].score);
}
//输出结果:
//1005 95
//2390 95
//1000 90
//3239 88
//7231 84
return 0;
}
string字符串
\(string\)是\(c++\)标准库提供的字符串类,用于便捷的管理和操作字符串。
string的定义与初始化
string s1 = "hello"; //将s1初始化为hello
string s2("hello"); //将s2初始化为hello
//string s3(n, c); //将s3初始化为n个字符c
string s3(5, 'a'); //s3的值为aaaaa
string的输入与输出
\(string\)的输入与输出需要使用\(cin\)和\(cout\),不能用\(scanf\)和\(printf\)
输入
1、cin
会忽略开头的制表符、换行符、空格,当再次碰到空白字符就停止(并不会读取空字符)
string s1;
cin >> s1;
cout << s1;
//输入hello world,输出hello,因为读入时,碰到中间的空格,就停止了
2、getline()
格式:getline(cin, s); //cin指的是读入流,一般情况下直接写cin即可,s是存储字符串的变量
getline会读入整个句子(连空格一起读入)
string s1;
//输入hello world,输出hello world
//因为连中间空格一起读入了
getline(cin, s1);
cout << s1;
输出
直接用\(cout\)输出即可
string常用操作
| 操作 | 含义 |
|---|---|
| s.empty() | 如果s为空串,则返回 true,否则返回 false |
| s.size() | 返回s中字符的个数,与s.length()用法一致 |
| s[i] | s中下标为i的字符,下标从 0 开始计数(可对其进行读写操作) |
| s1 = s2 | 把 s1 内容替换为 s2 的副本,即赋值 |
| s3 = s1 + s2 | 把 s2 连到 s1 之后生成一个新字符串,赋值给 s3 |
| s1==s2 | 比较 s1 与 s2 的内容,相等则返回 true,否则返回 false |
| !=, <, >, <=, >= | 按照字典序比较两个字符串,例如: if (s1 > s2) |
| s.insert(pos,s2) | 在 s 下标为 pos 的元素前插入 string 类型 s2 |
| s.substr(pos, len) | 返回一个 string 类型,它包含 s 中下标为 pos 起的连续 len 个字符构成的子串 |
| s.erase(pos, len) | 删除s中下标为 pos 开始的 len 个字符 |
| s.replace(pos, len, s2) | 将 s 中下标为 pos 开始的连续 len 个字符替换为 s2 |
| s.find(s2, pos) | 返回在 s 中以 pos 下标起查找 s2 第一次出现的位置,如果未找到,返回 string::npos(也可以看成是有符号整型的 -1) |
| s.c_str() | 返回一个与 s 字面值相同的 C 语言风格的字符串(可以先简单理解为字符数组) |
示例:
#include <bits/stdc++.h>
using namespace std;
int main()
{
string s1;
s1 = "abcde";
printf("%d\n", s1.size()); //输出5
s1[2] = 'f';
cout << s1 << endl; //输出abfde
s1 = "abcde";
s1.insert(1, "xyz");
cout << s1 << endl; //输出axyzbcde
s1 = "abcde";
string s2 = s1.substr(1, 2);
cout << s2 << endl; //输出bc
s1 = "abcde";
s1.erase(1, 2);
cout << s1 << endl; //输出ade
s1 = "abcde";
s1.replace(1, 3, "xy");
cout << s1 << endl; //输出axye
s1 = "abcde";
int x = s1.find("cd", 0);
cout << x << endl; //输出2
x = s1.find("ab", 3);
cout << x << endl; //输出-1
return 0;
}
vector容器
定义与本质
- Vector是C++ STL中的动态数组,支持元素的动态扩容和随机访问
- 底层通过连续内存存储元素,类似数组,但可以自动管理内存
初始化
vector<int> a; //空的容器
vector<int> b(5); //长度为5,默认值为0
vector<int> c(5, 3); //长度为5,初始值3
常用操作
常用操作
| 函数 | 功能描述 | 时间复杂度 |
|---|---|---|
[] |
通过下标访问元素,a[i] | O(1) |
front() |
访问首元素 | O(1) |
back() |
访问尾元素 | O(1) |
push_back(x) |
在尾部添加元素 | O(1) 均摊 |
pop_back() |
删除尾部元素 | O(1) |
clear() |
清空所有元素 | O(n) |
empty() |
返回一个\(bool\)值,判断是否为空 | O(1) |
size() |
返回当前元素个数 | O(1) |
capacity() |
返回容器的容量,即当前已为多少个元素分配了空间 | O(1) |
reserve(n) |
预分配至少\(n\)个元素的空间,避免频繁扩容 | O(n) |
resize(n) |
调整大小为\(n\),新增元素默认初始化 | O(n) |
#include <bits/stdc++.h>
using namespace std;
int main()
{
vector<char> v;
printf("%d\n", v.size()); //输出0
v.push_back('a');
v.push_back('b');
v.push_back('c');
v.push_back('d');
v.push_back('e');
printf("%c %c\n", v.front(), v.back()); //输出a e
printf("%d\n", v.size()); //输出5
//遍历容器元素
for(int i=0; i<v.size(); i++)
{
printf("%c ", v[i]);
}
printf("\n");
v.resize(10);
printf("%d\n", v.size()); //输出10
//遍历容器元素
for(char c : v)
{
printf("%c ", c);
}
return 0;
}
pair
定义
- \(pair\)用于存储两个不同或相同类型的数据
- 本质是将两个变量“打包”成一个整体,方便作为单个变量传递
声明与初始化
1、格式:\(pair\)<类型1,类型2> 变量名
2、初始化:
| 初始化方式 | 代码示例 | 说明 |
|---|---|---|
| 默认初始化 | pair<int, string> p; |
first和second为对应类型的默认值(int为0,string为空) |
| 构造函数初始化 | pair<int, string> p(101, "Alice"); |
直接传入两个值,顺序对应first、second |
make_pair 函数 |
pair<int, string> p; p = make_pair(101, "Alice"); |
先定义,再赋值 |
| 列表初始化(C++11+) | pair<int, string> p = {101, "Alice"}; |
简洁直观,奥赛中最常用 |
//构造函数初始化
pair<int, string> p1(101, "Alice");
//make_pair初始化
pair<int, string> p2;
p2 = make_pair(102, "Bob");
//列表初始化
pair<int, string> p3 = {103, "charlie"};
赋值操作与成员访问
整体赋值: 两个\(pair\)类型完全匹配时,可直接用=赋值
成员单独赋值: 通过\(first\)和\(second\)直接修改单个成员
- first: 访问第一个元素(对应模板的“类型1”)
- second: 访问第二个元素(对应模板的“类型2”)
#include <bits/stdc++.h>
using namespace std;
int main()
{
pair<int, string> p1(101, "Alice");
pair<int, string> p2;
p2 = p1;
cout << p2.first << endl;
cout << p2.second << endl;
p2.first = 102;
p2.second = "Bob";
cout << p2.first << endl;
cout << p2.second << endl;
return 0;
}
比较运算和交换操作
\(pair\)支持比较运算和交换操作,这是其在排序、容器中应用的核心基础
比较运算
\(pair\)重载了\(<、<=、>、>=、==、!=\)运算符,默认比较规则为“先比first,再比second”,即:优先按第一关键字排序,再按第二关键字排序
#include <bits/stdc++.h>
using namespace std;
int main()
{
pair<int, int> p1 = {2, 3};
pair<int, int> p2 = {2, 5};
pair<int, int> p3 = {1, 10};
// 比较结果
cout << (p1 < p2) << endl; // 1(true:first相同,p1.second=3 < p2.second=5)
cout << (p1 > p3) << endl; // 1(true:p1.first=2 > p3.first=1)
cout << (p2 == p3) << endl; // 0(false:first和second均不同)
return 0;
}
交换操作
使用\(swap()\)函数交换两个类型完全相同的\(pair\)的所有成员(first和second同时交换)
#include <bits/stdc++.h>
using namespace std;
int main()
{
pair<int, string> p1 = {101, "Alice"};
pair<int, string> p2 = {102, "Bob"};
p1.swap(p2); //交换p1和p2
cout << p1.first << " " << p1.second << endl; //102 Bob
cout << p2.first << " " << p2.second << endl; //101 Alice
return 0;
}
高精度
高精度计算,也被称作大整数计算,运用了一些算法结构来支持更大整数间的运算(数字大小超过语言内建整型(\(int\) ,\(long long\)))。
反转存储
在平常的实现中,高精度数字利用字符串表示,每一个字符表示数字的一个十进制位。因此,可以说,高精度数值计算实际上是一种特别的字符串处理。
读入字符串时,数字最高位在字符串首(下标小的位置)。但习惯上,下标最小的位置存放的是数字的最低位,即存储反转的字符串。
这么做的原因在于,数字的长度可能发生变化,但我们希望同样权值位始终保持对齐(例如,希望所有的个位都在下标[1],所有的十位都在下标[2]...)。
同时,加、减、乘的运算一般都从个位开始进行(回想小学的竖式运算)。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3000;
char s1[maxn] = {};
int a[maxn] = {};
int main()
{
int len = 0;
scanf("%s", s1);
//将字符串s1反转存储到a数组
len = strlen(s1);
a[0] = len; //a[0]存储整个字符串的长度
for(int i=1; i<=len; i++)
{
a[i] = s1[len - i] - '0'; //反转存储
}
//将反转存储的数组进行输出
for(int i=1; i<=a[0]; i++)
{
printf("%d", a[i]);
}
return 0;
}
高精加法
高精度加法,其实就是竖式加法。
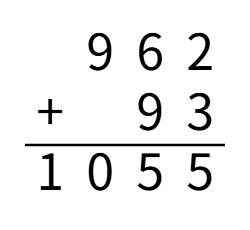
也就是从最低位开始,将两个加数对应位置上的数码相加,并判断是否达到或超过10。
如果达到,那么处理进位:
将更高一位的结果上增加1,当前位的结果减少10。
//高精+高精
void GaddG(char s1[], char s2[], int c[])
{
int a[maxn] = {}, b[maxn] = {};
int len1 = strlen(s1);
int len2 = strlen(s2);
//反转存储
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
int len3 = max(len1, len2);
for(int i=1; i<=len3; i++)
{
c[i] += a[i] + b[i];
c[i+1] = c[i] / 10; //进位
c[i] %= 10; //余数即为当前位
}
if(c[len3+1] > 0) len3++;
c[0] = len3;
}
高精减法
高精度减法,也就是竖式减法
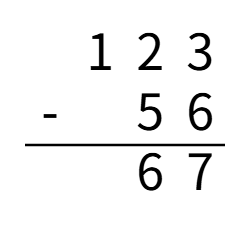
从个位起逐位相减,遇到负的情况则向上一位借1。整体思路与加法完全一致。
//高精 - 高精
void GjianG(char s1[], char s2[], int c[])
{
int a[maxn] = {}, b[maxn] = {};
int len1 = strlen(s1);
int len2 = strlen(s2);
//首先判断结果的正负
if(len1<len2 || (len1==len2 && strcmp(s1, s2)<0))
{
printf("-");
swap(s1, s2);
}
//反转存储
len1 = strlen(s1);
len2 = strlen(s2);
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
int len3 = max(len1, len2);
for(int i=1; i<=len3; i++)
{
c[i] += a[i] - b[i];
if(c[i] < 0)
{
c[i+1]--; //向高位借1
c[i] += 10; //当前为加10
}
}
//删除前导0,注意这里至少要保留1位
//当结果为0时,也要输出0
while(len3>1 && c[len3]==0) len3--;
c[0] = len3;
}
高精乘法
高精乘低精
高精乘低精,用低精数和高精的每一位\(i\)相乘,向\(i+1\)进位
注意:当乘到最后一位(\(len\))时,可能会向\(len+1\)及以后进位(当进位到\(len+1\)时,超过进制的最大值时,便向\(len+2\)及以后进位)
void GchengD(int a[], int k)
{
int x = 0;
for(int i=1; i<=a[0]; i++)
{
a[i] = a[i] * k + x;
x = a[i] / 10;
a[i] = a[i] % 10;
}
while(x)
{
a[++a[0]] = x % 10;
x /= 10;
}
}
高精乘高精
高精度乘法,也是竖式乘法
a₄ a₃ a₂ a₁
* b₃ b₂ b₁
—————————————————————————————
C₄' C₃' C₂' C₁'
C₅'' C₄'' C₃'' C₂''
C₆''' C₅''' C₄''' C₃'''
—————————————————————————————————
C₆ C₅ C₄ C₃ C₂ C₁
\(c_i\) = \(c_i\)' + \(c_i\)'' + \(c_i\)'''
以\(c_3\)为例:
\(c_3\) = \(c_3\)' + \(c_3\)'' + \(c_3\)'''
\(c_3\)' = \(a_3\) * \(b_1\)
\(c_3\)'' = \(a_2\) * \(b_2\)
\(c_3\)''' = \(a_1\) * \(b_3\)
观察规律可知:\(a_i\) * \(b_j\)的值都累加到了\(c_{i+j-1}\),进位到了\(c_{i+j}\)。
//高精乘高精
void GchengG(char s1[], char s2[], int c[])
{
int a[maxn] = {}, b[maxn] = {};
int len1 = strlen(s1);
int len2 = strlen(s2);
//反转存储
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
for(int i=1; i<=len1; i++)
{
for(int j=1; j<=len2; j++)
{
c[i+j-1] += a[i] * b[j]; //a[i] * b[j]的值累加到c[i+j-1]
c[i+j] += c[i+j-1] / 10; //向c[i+j]进位
c[i+j-1] %= 10;
}
}
//删除前导0
int len3 = len1 + len2;
while(len3>1 && c[len3]==0) len3--;
c[0] = len3;
}
高精除法
高精除低精
竖式除法
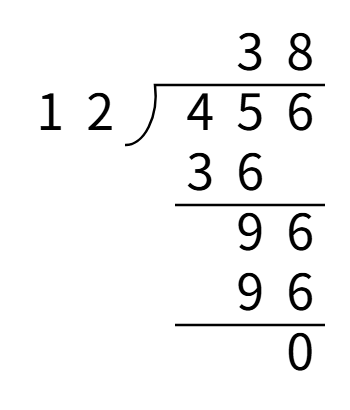
除法运算不要反转存储,因为除法运算是从高位开始除。
从最高位开始除,相除后的结果保存在该位,余数*10后,累加到下一位再继续除
//高精除低精
//c为商,d为余数
void GchuD(char s1[], int b, int c[], int &d)
{
int a[maxn] = {};
int t[maxn] = {};
int len1 = strlen(s1);
//正向存储
for(int i=1; i<=len1; i++) a[i] = s1[i-1] - '0';
//从高位开始除
int x = 0;
for(int i=1; i<=len1; i++)
{
t[i] = (x*10+a[i]) / b;
x = (x*10+a[i]) % b;
}
d = x;
//前导可能为0,st记录第一个非0的位置
int st = 1;
while(t[st]==0 && st<len1) st++;
//将结果保存到c数组
c[0] = 0;
for(int i=st; i<=len1; i++) c[++c[0]] = t[i];
}
高精除高精
高精除高精依然使用竖式长除法
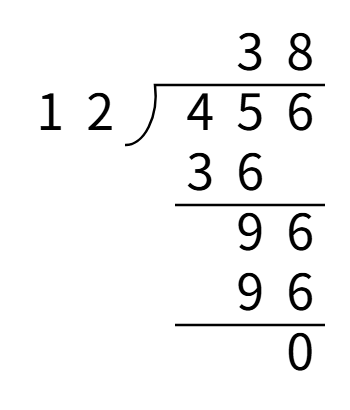
竖式长除法实际上可以看作一个逐次减法的过程。
例如上图中商数十位的计算可以这样理解:将\(45\)减去三次\(12\)后变得小于\(12\),不能再减,故此位为\(3\)。
因此可以把除法转变为多次减法,减完后剩余的数即为余数。
//比较字符串a[k, k+len-1]和b的大小
//即a从下标k开始,长度为len
//a>=b返回true,a<b返回false
bool compare(int a[], int b[], int k, int len)
{
if(a[k+len] > 0) return true; //字符串a上面那位还有值,则一定比b大
for(int i=len-1; i>=0; i--)
{
if(a[k+i] > b[i+1]) return true; //明确a>b
else if(a[k+i] < b[i+1]) return false; //明确a<b
}
return true; //每一位都相等,则表示a和b相等
}
//高精除高精
//运算成功返回true,失败返回false
bool GchuG(char s1[], char s2[], int c[], int d[])
{
int a[maxn] = {}, b[maxn] = {};
int len1 = strlen(s1);
int len2 = strlen(s2);
//除数为0
if(len2==0 && s2[0]==0) return false;
//反向存储,因为后面要用到高精减法
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
//从a[len1-len2+1,len1]开始减
for(int i=len1-len2+1; i>=1; i--)
{
//只要a[i, i+len2-1]大于等于b,就不断地减b
while(compare(a, b, i, len2))
{
//高精减
for(int j=0; j<len2; j++)
{
a[i+j] -= b[j+1];
if(a[i+j] < 0)
{
a[i+j+1] -= 1;
a[i+j] += 10;
}
}
c[i] += 1;
}
}
//c保存的是商,此处是计算商的长度
for(int i=len1-len2+1; i>=1; i--)
{
if(c[i] != 0)
{
c[0] = i;
break;
}
}
if(c[0] == 0) c[0] = 1; //处理商为0的情况,长度设为1,其余均为0
//a中剩下的数字即为余数,复制到r中
for(int i=len1; i>=1; i--)
{
if(a[i] != 0) //d数组的初值都是0,所以a[i]为0时不用赋值
{
d[i] = a[i];
if(d[0] == 0) d[0] = i; //计算余数的长度
}
}
if(d[0]==0) d[0] = 1; //处理余数为0的情况,长度设为1,其余均为0
return 0;
}
四则运算
完整的四则运算代码,高精加、高精减、高精乘、高精除低精、高精除高精
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3000;
int ans[maxn] = {}, r[maxn] = {}, z = 0;
//高精 + 高精
void GaddG(char s1[], char s2[], int c[])
{
int a[maxn] = {}, b[maxn] = {};
int len1 = strlen(s1);
int len2 = strlen(s2);
//反转存储
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
int len3 = max(len1, len2);
for(int i=1; i<=len3; i++)
{
c[i] += a[i] + b[i];
c[i+1] = c[i] / 10; //进位
c[i] %= 10; //余数即为当前位
}
if(c[len3+1] > 0) len3++;
c[0] = len3;
}
//高精 - 高精
void GjianG(char s1[], char s2[], int c[])
{
int a[maxn] = {}, b[maxn] = {};
int len1 = strlen(s1);
int len2 = strlen(s2);
//首先判断结果的正负
if(len1<len2 || (len1==len2 && strcmp(s1, s2)<0))
{
printf("-");
swap(s1, s2);
}
//反转存储
len1 = strlen(s1);
len2 = strlen(s2);
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
int len3 = max(len1, len2);
for(int i=1; i<=len3; i++)
{
c[i] += a[i] - b[i];
if(c[i] < 0)
{
c[i+1]--; //向高位借1
c[i] += 10; //当前为加10
}
}
//删除前导0,注意这里至少要保留1位
//当结果为0时,也要输出0
while(len3>1 && c[len3]==0) len3--;
c[0] = len3;
}
//高精乘高精
void GchengG(char s1[], char s2[], int c[])
{
int a[maxn] = {}, b[maxn] = {};
int len1 = strlen(s1);
int len2 = strlen(s2);
//反转存储
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
for(int i=1; i<=len1; i++)
{
for(int j=1; j<=len2; j++)
{
c[i+j-1] += a[i] * b[j]; //a[i] * b[j]的值累加到c[i+j-1]
c[i+j] += c[i+j-1] / 10; //向c[i+j]进位
c[i+j-1] %= 10;
}
}
//删除前导0
int len3 = len1 + len2;
while(len3>1 && c[len3]==0) len3--;
c[0] = len3;
}
//高精除低精
//c为商,d为余数
void GchuD(char s1[], int b, int c[], int &d)
{
int a[maxn] = {};
int t[maxn] = {};
int len1 = strlen(s1);
//正向存储
for(int i=1; i<=len1; i++) a[i] = s1[i-1] - '0';
//从高位开始除
int x = 0;
for(int i=1; i<=len1; i++)
{
t[i] = (x*10+a[i]) / b;
x = (x*10+a[i]) % b;
}
d = x;
//前导可能为0,st记录第一个非0的位置
int st = 1;
while(t[st]==0 && st<len1) st++;
//将结果保存到c数组
c[0] = 0;
for(int i=st; i<=len1; i++) c[++c[0]] = t[i];
}
//比较字符串a[k, k+len-1]和b的大小
//即a从下标k开始,长度为len
//a>=b返回true,a<b返回false
bool compare(int a[], int b[], int k, int len)
{
if(a[k+len] > 0) return true; //字符串a上面那位还有值,则一定比b大
for(int i=len-1; i>=0; i--)
{
if(a[k+i] > b[i+1]) return true; //明确a>b
else if(a[k+i] < b[i+1]) return false; //明确a<b
}
return true; //每一位都相等,则表示a和b相等
}
//高精除高精
//运算成功返回true,失败返回false
bool GchuG(char s1[], char s2[], int c[], int d[])
{
int a[maxn] = {}, b[maxn] = {};
int len1 = strlen(s1);
int len2 = strlen(s2);
//除数为0
if(len2==0 && s2[0]==0) return false;
//反向存储,因为后面要用到高精减法
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
//从a[len1-len2+1,len1]开始减
for(int i=len1-len2+1; i>=1; i--)
{
//只要a[i, i+len2-1]大于等于b,就不断地减b
while(compare(a, b, i, len2))
{
//高精减
for(int j=0; j<len2; j++)
{
a[i+j] -= b[j+1];
if(a[i+j] < 0)
{
a[i+j+1] -= 1;
a[i+j] += 10;
}
}
c[i] += 1;
}
}
//c保存的是商,此处是计算商的长度
for(int i=len1-len2+1; i>=1; i--)
{
if(c[i] != 0)
{
c[0] = i;
break;
}
}
if(c[0] == 0) c[0] = 1; //处理商为0的情况,长度设为1,其余均为0
//a中剩下的数字即为余数,复制到r中
for(int i=len1; i>=1; i--)
{
if(a[i] != 0) //d数组的初值都是0,所以a[i]为0时不用赋值
{
d[i] = a[i];
if(d[0] == 0) d[0] = i; //计算余数的长度
}
}
if(d[0]==0) d[0] = 1; //处理余数为0的情况,长度设为1,其余均为0
return 0;
}
int main()
{
char s1[maxn], s2[maxn];
// scanf("%s%s", s1, s2);
// GaddG(s1, s2, ans);
// for(int i=ans[0]; i>=1; i--)
// {
// printf("%d", ans[i]);
// }
// scanf("%s%s", s1, s2);
// GjianG(s1, s2, ans);
// for(int i=ans[0]; i>=1; i--)
// {
// printf("%d", ans[i]);
// }
// scanf("%s%s", s1, s2);
// GchengG(s1, s2, ans);
// for(int i=ans[0]; i>=1; i--)
// {
// printf("%d", ans[i]);
// }
// int x = 0;
// scanf("%s%d", s1, &x);
// GchuD(s1, x, ans, z);
// for(int i=1; i<=ans[0]; i++)
// {
// printf("%d", ans[i]);
// }
// printf("\n%d", z);
scanf("%s%s", s1, s2);
GchuG(s1, s2, ans, r);
for(int i=ans[0]; i>=1; i--)
{
printf("%d", ans[i]);
}
printf("\n");
//余数
for(int i=r[0]; i>=1; i--)
{
printf("%d", r[i]);
}
return 0;
}
压位高精度
引入:
在一般的高精度加法、减法、乘法运算中,我们都是将参与运算的数拆分成一个个单独的数码进行运算。
例如计算\(8192*42\)时,如果按照高精度乘高精度的计算方式,我们实际上算的是\((8000+100+90+2)*(40+2)\)。
在位数较多的时候,拆分出的数也很多,高精度运算的效率就会下降。
优化:
注意到拆分数字的方式并不影响最终的结果,因此我们可以将若干个数码进行合并。
过程:
还是以上面的例子为例,如果我们每两位拆分一个数,我们可以拆分成\((8100+92)*42\).
这样的拆分不影响最终结果,但是因为拆分出的数字变少了,计算效率也就提升了。
进位制:
从进位制的角度理解这一过程,我们通过在较大的进位制(上面每两位拆分一个数,可以认为是在\(100\)进制下进行运算)下进行运算,从而达到减少参与运算的数字的位数,提升运算效率的目的。
压位高精加法:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3000;
int ans[maxn] = {}, r[maxn] = {};
//压位高精度(百进制)
//高精 + 高精
void GaddG(char s1[], char s2[], int c[])
{
int a[maxn] = {}, b[maxn] = {}; //十进制
int a1[maxn] = {}, b1[maxn] = {}; //百进制
int len1 = strlen(s1);
int len2 = strlen(s2);
//反转存储(十进制)
for(int i=1; i<=len1; i++) a[i] = s1[len1-i] - '0';
for(int i=1; i<=len2; i++) b[i] = s2[len2-i] - '0';
//反转存储(百进制)
len1 = (len1 + 1) / 2;
len2 = (len2 + 1) / 2;
for(int i=1; i<=len1; i++) a1[i] = a[1+2*(i-1)+1] * 10 + a[1+2*(i-1)];
for(int i=1; i<=len2; i++) b1[i] = b[1+2*(i-1)+1] * 10 + b[1+2*(i-1)];
//百进制格式下进行加法
int len3 = max(len1, len2);
for(int i=1; i<=len3; i++)
{
c[i] += a1[i] + b1[i];
c[i+1] = c[i] / 100; //进位
c[i] %= 100; //余数即为当前位
}
if(c[len3+1] > 0) len3++;
c[0] = len3;
}
int main()
{
char s1[maxn], s2[maxn];
scanf("%s%s", s1, s2);
GaddG(s1, s2, ans);
//按百进制输出
printf("%d", ans[ans[0]]);
for(int i=ans[0]-1; i>=1; i--)
{
printf("%02d", ans[i]);
}
return 0;
}
栈和队列
栈
一些概念
栈是\(OI\)中常用的一种线性数据结构。
注意: 本文主要讲的是栈这种数据结构,而非程序运行时的系统栈/栈空间。
特点: 栈的修改与访问是按照后进先出的原则进行的,因此栈通常被称为是后进先出表,简称\(LIFO\)表。
举例来讲:
可以把食堂里洗净的一摞碗看做一个栈,通常情况下,最先洗净的碗总是放在最底下,后洗净的碗总是摞在最顶上。
而使用时,却是从顶上拿取,也就是说,后洗的先取用,后摞上的先取用。
如果我们把洗净的碗“摞上”称为进栈,把“取用碗”称为出栈,那么,上例的特点是:后进栈的先出栈。
用图形来表示:
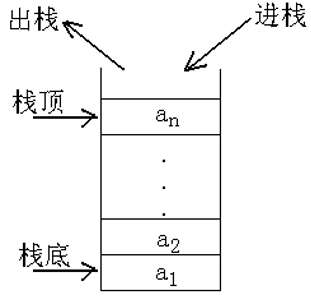
常见运算:
- 进栈: 往栈顶加入一个元素
- 出栈:删除栈顶元素
- 读栈:查看当前的栈顶元素
- 建栈:在使用栈之前,首先需要建立一个空栈
- 测试栈:使用栈的过程中,不断测试栈是否为空或已满
用数组模拟栈
//st表示栈,top为栈顶元素下标
int st[maxn] = {}, top = 0;
//进栈
st[++top] = x;
//读栈
int y = st[top];
//出栈
if(top) top--;
//清空栈
top = 0;
STL中的栈
stack<int> s;
s.empty(); //如果栈为空,返回true,否则返回false
s.size(); //返回栈中元素的个数
s.pop(); //删除栈顶元素但不返回其值
s.top(); //返回栈顶的元素,但不删除该元素
s.push(); //在栈顶压入新元素
//清空栈
while(!s.empty()) s.pop();
例题:
B3614 【模板】栈
数组模拟实现:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 10;
int n = 0;
long long st[maxn] = {}, top = 0;
int main()
{
string s1;
int x = 0;
while(scanf("%d", &n) != EOF)
{
top = 0; //清空栈
for(int i=1; i<=n; i++)
{
cin >> s1;
if(s1 == "push")
{
cin >> x;
st[++top] = x; //进栈
}
if(s1 == "pop")
{
if(top > 0) top--; //出栈
else cout << "Empty" << endl;
}
if(s1 == "query")
{
if(top > 0) cout << st[top] << endl;//读栈
else cout << "Anguei!" << endl;
}
if(s1 == "size") cout << top << endl; //栈的大小
}
}
return 0;
}
STL实现:
#include <bits/stdc++.h>
using namespace std;
int n = 0;
stack<long long> st;
int main()
{
string s1;
int x = 0;
while(cin >> n)
{
while(st.size()) st.pop();
while(n--)
{
cin >> s1;
if(s1 == "push")
{
cin >> x;
st.push(x);
}
if(s1 == "pop")
{
if(st.size() == 0) cout << "Empty" << endl;
else st.pop();
}
if(s1 == "query")
{
if(st.size() == 0) cout << "Anguei!" << endl;
else cout << st.top() << endl;
}
if(s1 == "size") cout << st.size() << endl;
}
}
return 0;
}
队列
一些概念
队列: 是一种具有先进入队列的元素一定先出队列性质的表。由于该性质,队列通常也被称为先进先出表,简称\(FIFO\)表。
举例来讲:
就像排队买东西,排在前面的人先买完东西后离开队伍(删除),而后来的人总是排在队伍末尾(插入)。
通常把队列的删除和插入分别称为出队和入队。
用图形来表示:
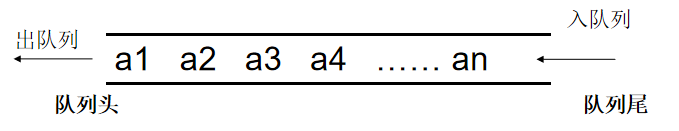
常见运算:
- 入队:将x接到队列的末端
- 出队:弹出队列的第一个元素,注意,并不会返回被弹出元素的值
- 访问队首元素:返回最早被压入队列的元素
- 访问队尾元素:返回最后被压入队列的元素
- 判断是否为空
- 访问队列中的元素个数
用数组模拟队列
int q[maxn] = {}, head = 1, tail = 0;
q[++tail] = x; //插入元素
head++; //删除元素
x = q[head]; //访问队首
x = q[tail]; //访问队尾
//清空队列
head = 1;
tail = 0;
head > tail; //队列为空
x = tail - head + 1; //队列中的元素个数
STL中的队列
queue<int> q;
q.front(); //返回队首元素
q.back(); //返回队尾元素
q.push(); //在队尾插入元素
q.pop(); //弹出队首元素
q.empty(); //队列是否为空
q.size(); //返回队列中元素的个数
//清空队列
while(!q.empty()) q.pop();
//queue赋值运算符:=
queue<int> q1, q2;
q1 = q2; //将q2赋值给q1
例题:
B3616 【模板】队列
数组模拟实现:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10010;
int n = 0;
int q[maxn] = {}, head = 1, tail = 0;
int main()
{
int op = 0, x = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &op);
if(op == 1) //将元素 x 加入队列
{
scanf("%d", &x);
q[++tail] = x;
}
if(op == 2) //将队首弹出队列
{
if(head > tail) printf("ERR_CANNOT_POP\n");
else head++;
}
if(op == 3) //查询队首
{
if(head > tail) printf("ERR_CANNOT_QUERY\n");
else printf("%d\n", q[head]);
}
if(op == 4) //查询队列内元素个数
{
printf("%d\n", tail - head + 1);
}
}
return 0;
}
STL实现:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10010;
int n = 0;
queue<int> q;
int main()
{
int op = 0, x = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &op);
if(op == 1) //将元素 x 加入队列
{
scanf("%d", &x);
q.push(x);
}
if(op == 2) //将队首弹出队列
{
if(q.size() == 0) printf("ERR_CANNOT_POP\n");
else q.pop();
}
if(op == 3) //查询队首
{
if(q.size() == 0) printf("ERR_CANNOT_QUERY\n");
else printf("%d\n", q.front());
}
if(op == 4) //查询队列内元素个数
{
printf("%d\n", q.size());
}
}
return 0;
}
搜索和回溯
说明
搜索与回溯是计算机解题中常用的算法,很多问题无法根据某种确定的计算法则来求解,可以利用搜索与回溯的技术求解。
回溯是搜索算法中的一种控制策略。
基本思想:
为了求得问题的解,先选择某一种可能情况向前探索,在探索过程中,一旦发现原来的选择时错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或证明无解。
比如:迷宫问题
进入迷宫后,先随意选择一个前进方向,一步步向前试探前进,如果碰到死胡同,说明前进方向已无路可走,这时,首先看其他方向是否还有路可走,如果有路可走,则沿该方向再向前试探;如果已无路可走,则返回一步,再看其他方向是否还有路可走;如果有路可走,则沿该方向再向前试探。
按此原则不断搜索回溯再搜索,直到找到新的出路或从原路返回入口处无解为止。
具体例子:
在下图中找一条A到B的路线
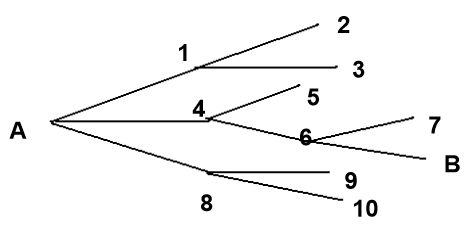
从A到B的路线:A->4->6->B
补充:exit()函数
1、作用:直接结束整个程序,多用于在搜索时,如果找到最终结果,直接退出程序,而不需要再层层返回。
2、函数原型
void exit(int status);
3、status是一个整数类型的退出状态码,用于告诉操作系统程序退出结果
EXIT_SUCCESS:等价与0,表示程序正常、成功退出(最常用)
EXIT_FAILURE:等价于非0整数(通常是1),表示程序异常、失败退出
也可以直接传入整数0(代替EXIT_SUCCESS)或非0整数(代替EXIT_FAILURE)。
竞赛中exit(0);是最简洁、最常用的写法
框架
框架一:
int search(int k)
{
for(int i=1; i<=算符种数; i++)
{
if(满足条件)
{
保存结果;
if(到目的地) 输出解;
else search(k + 1);
恢复:保存结果之前的状态{回溯一步}
}
}
}
框架二:
int search(int k)
{
if(到目的地)
{
输出解;
return 0;
}
for(int i=1; i<=算符种数; i++)
{
if(满足条件)
{
保存结果;
search(k + 1);
恢复:保存结果之前的状态{回溯一步}
}
}
}
例题
P198. 全排列问题
写法一:
#include <bits/stdc++.h>
using namespace std;
int n = 0;
int a[15] = {}, v[15] = {};
//给第x位填数
void search(int x)
{
for(int i=1; i<=n; i++)
{
if(v[i] == 1) continue; //i已被使用,跳过
v[i] = 1; //标记i已使用
a[x] = i; //第x位赋上值i
if(x == n) //已完成全部赋值
{
for(int j=1; j<=n; j++)
{
printf("%5d", a[j]);
}
printf("\n");
}
search(x + 1); //搜索
v[i] = 0; //回溯,只需要标记i未用即可,a[x]不需要
}
}
int main()
{
scanf("%d", &n);
search(1); //从第1位开始搜索
return 0;
}
写法二:
#include <bits/stdc++.h>
using namespace std;
int n = 0;
int a[15] = {}, v[15] = {};
//给第x位填数
void search(int x)
{
if(x > n)
{
for(int j=1; j<=n; j++)
{
printf("%5d", a[j]);
}
printf("\n");
return;
}
for(int i=1; i<=n; i++)
{
if(v[i] == 1) continue; //i已被使用,跳过
v[i] = 1; //标记i已使用
a[x] = i; //第x位赋上值i
search(x + 1); //搜索
v[i] = 0; //回溯,只需要标记i未用即可,a[x]不需要
}
}
int main()
{
scanf("%d", &n);
search(1); //从第1位开始搜索
return 0;
}
分治算法
二分法
二分查找
定义:
二分查找,也叫折半搜索、对数搜索,是用来在一个有序数组中查找某一元素的算法。
过程:
以在一个升序数组中查找一个数为例。
每次比较数组当前部分的中间元素,如果中间元素大于等于所查找的值同理,只需到左侧查找;如果中间元素小于所查找的值,那么左侧的只会更小,不会有所查找的元素,只需到右侧查找。
时间复杂度:
平均时间复杂度和最坏时间复杂度均为\(O(log(n))\)。
因为在二分搜索过程中,算法每次都把查询的区间减半,所以对于一个长度为\(n\)的数组,至多会进行\(O(log(n))\)次查找。
代码模板:
bool check(int x) //检查x是否满足某种性质
int l = 1, r = n, ans = 0;
while(l <= r)
{
int mid = (l+r)>>1;
if(check(mid)) { ans = mid; r = mid - 1; }
else l = mid + 1;
}
printf("%d", ans);
例题: PJ835 二分查找
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 10;
int n = 0;
int a[maxn] = {};
bool check(int pos, int x)
{
return a[pos] >= x;
}
int main()
{
int x = 0, ans = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
scanf("%d", &x);
int l = 1, r = n;
while(l <= r)
{
int mid = (l + r) >> 1;
if(check(mid, x)) { ans = mid; r = mid - 1; }
else { l = mid + 1; }
}
if(a[ans] == x) printf("%d ", ans);
else printf("-1 ");
return 0;
}
STL的二分查找
c++标准库中的两个函数
lower_bound: 查找首个大于等于给定值的元素,返回其指针(内存地址)
upper_bound: 查找首个大于给定值的元素,返回其指针(内存地址)
例题: PJ835 二分查找
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 10;
int n = 0;
int a[maxn] = {};
int main()
{
int x = 0, ans = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
scanf("%d", &x);
ans = lower_bound(a+1, a+1+n, x) - a;
if(a[ans] == x) printf("%d ", ans);
else printf("-1 ");
return 0;
}
最大值最小化
概念:
如果一个数组中的左侧或者右侧都满足某一种条件,而另一侧都不满足这种条件,也可以看作是一种有序。
换言之,二分查找可以用来查找满足某种条件的最大(最小)的值。
思想:
求满足某种条件的最大值的最小可能情况(最大值最小化)。
暴力: 从小到大枚举这个作为答案的最大值,然后去判断是否合法。
优化做法:
前提: 答案具有单调性
条件:
- 答案在一个固定区间内
- 可能查找一个符合条件的值不是很容易,但要求能比较容易得判断某个值是否是符合条件的
- 可行解对于区间满足一定的单调性,换言之,如果\(x\)是符合条件的,那么有\(x+1\)或者\(x-1\)也符合条件。
例题: P2440 木材加工
#include <bits/stdc++.h>
using namespace std;
/*
求最小值最大问题,考虑二分答案
1、切割够的木头长度介于1~max(原木最大长度)之间
2、如果mid满足条件,则去[mid+1, r]找,否则去[l,mid-1]找
*/
const int maxn = 1e5 + 10;
int n = 0, k = 0;
int a[maxn], ans = 0;
//检查切割成x长度,是否满足
//若切成的段数>=k,则满足,返回true,否则返回false
bool check(int x)
{
int t = 0;
for(int i=1; i<=n; i++)
{
t += a[i] / x;
}
if(t >= k) return true;
return false;
}
int main()
{
int l = 1, r = 0;
scanf("%d%d", &n, &k);
for(int i=1; i<=n; i++)
{
scanf("%d", &a[i]);
r = max(r, a[i]);
}
//整数二分答案
while(l <= r)
{
int mid = (l + r) >> 1;
if(check(mid)) { ans = mid; l = mid + 1; }
else r = mid - 1;
}
printf("%d", ans);
return 0;
}
浮点数二分
一般如果题目要求精度为小数点后\(n\)位,则运算时,保存到\(n+2\)位即可。
即:题目要求精确到小数点后\(2\)位,运算时,保存到小数点后\(4\)位即可。
代码模板:
写法一:
const double eps = 1e-4;
bool check(double x) //检查x是否满足某种性质
double l = 1, r = n;
while(l + eps < r)
{
double mid = (l+r)/2;
if(check(mid)) r = mid;
else l = mid;
}
printf("%lf", l);
写法二:
double l = 1, r = n;
for(int i=1; i<=100; i++)
{
double mid = (l+r)/2;
if(check(mid)) r = mid;
else l = mid;
}
printf("%lf", l);
例题: PJ215 一元三次方程求解
#include <bits/stdc++.h>
using namespace std;
double a = 0, b = 0, c = 0, d = 0;
double f(double x)
{
return a*x*x*x + b*x*x + c*x + d;
}
int main()
{
int cnt = 0;
scanf("%lf%lf%lf%lf", &a, &b, &c, &d);
for(double i=-100; i<100; i++)
{
double y1 = f(i);
double y2 = f(i+1);
//先判断边界是不是答案
if(f(i) == 0)
{
printf("%.2lf ", i);
cnt++;
}
//如果y1*y1<0,表示f(i)和f(i+1)异号,则i到i+1之间一定有答案
else if(y1 * y2 < 0)
{
double l = i, r = i + 1, ans = 0;
while(l + 0.0001 < r )
{
double mid = (l+r)/2;
if(f(mid)*f(r) < 0) l = mid;
else r = mid;
}
printf("%.2lf ", l);
cnt++;
}
if(cnt == 3) return 0;
}
//前面没有判断100,如果cnt==2,则表示100一定是答案
if(cnt == 2) printf("%.2lf", 100);
return 0;
}
逆序数
逆序: 在一个排列中,如果某一个较大的数排在某一个较小的数前面,就说这两个数构成一个逆序或反序。
逆序数: 在一个排列里出现的逆序的总个数,叫做逆序数。
排列的逆序数是它恢复成正序序列所需要做相邻对换的最少次数。
解法: 求解逆序数的算法,可以使用归并排序或树状数组,时间复杂度均为\(O(nlogn)\)。此处只讲解归并排序法。
归并排序
原理: 归并排序基于分治思想将数组分段排序后再合并,合并是核心
时间复杂度:
时间复杂度在最优、最坏与平均情况下均为\(O(nlogn)\),空间复杂度为\(O(n)\)
稳定性: 归并排序是一种稳定排序算法
分段:
1、当数组长度为1时,不用再分解
2、当数组长度大于1时,将该数组分为两段,通常分为尽量等长的两段(\(\text{mid} = \left\lfloor \frac{l + r}{2} \right\rfloor\))
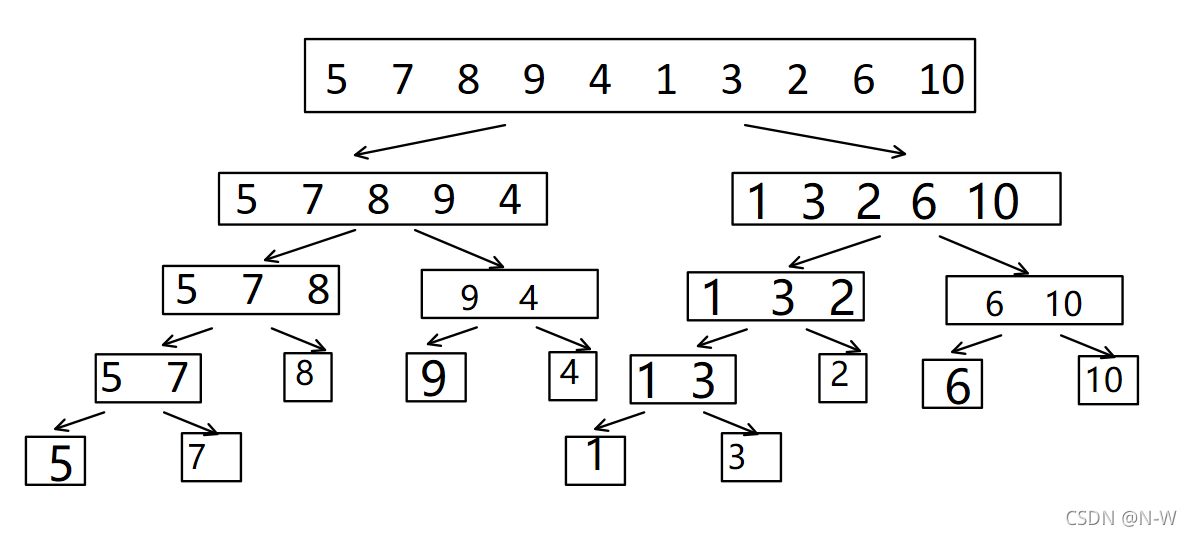
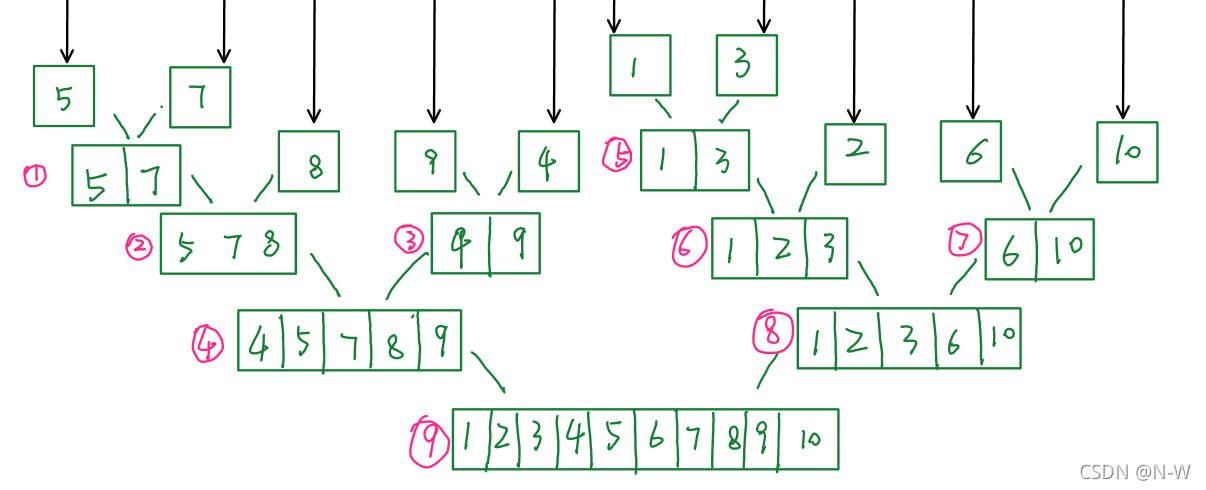
合并:
归并排序最核心的部分是合并过程:将两个有序的数组\(a[i]\)和\(b[j]\)合并为一个有序数组\(c[k]\)
从左往右枚举\(a[i]\)和\(b[j]\),找出最小的值并放入数组\(c[k]\);重复上述过程直到\(a[i]\)和\(b[j]\)有一个为空时,将另一个数组剩下的元素放入\(c[k]\)。
为保证排序的稳定性,前段首元素小于或等于后段首元素时(\(a[i]<=b[j]\)),而非小于时(\(a[i]<b[j]\))就要作为最小值放入\(c[k]\)。
代码模板:
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
//不断的细分,直到只有一个元素
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
//回溯时进行合并
//将[l, r]这段区间分为[l, mid]和[mid+1, r]两部分,边比较边放入临时数组
int k = 0, i = l, j = mid + 1;
while(i<=mid && j<=r)
{
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
//将前mid前或mid后的剩余元素加入临时数组
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
//将临时数组中的元素,放到原数组,位置是对应的,相当于对这一段进行了排序
for (i=l, j=0; i<=r; i++) q[i] = tmp[j++];
}
逆序对
逆序对 是\(i<j\)且\(a_i>a_j\)的有序数对\((i, j)\)。排序后的数组无逆序对。
求逆序对:
归并排序的合并操作中,每次后段首元素被作为当前最小值取出时,前段剩余元素个数之和即是逆序对,将合并过程中产生的所有逆序对个数相加,最后就是总的逆序对的数量。
void merge_sort(int q[], int l, int r)
{
if(l >= r) return;
int mid = (l + r) >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid+1, r);
int k = 0, i = l, j = mid + 1;
while(i<=mid && j<=r)
{
if(q[i] <= q[j]) tmp[++k] = q[i++];
else
{
tmp[++k] = q[j++];
ans += mid + 1 - i; //计算逆序对的数量
}
}
while(i <= mid) tmp[++k] = q[i++];
while(j <= r) tmp[++k] = q[j++];
for(i=l, j=1; i<=r; i++) q[i] = tmp[j++];
}
例题
PJ213 逆序对个数
#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e6+10;
int n = 0;
int a[maxn] = {}, tmp[maxn] = {};
long long ans = 0;
void merge_sort(int q[], int l, int r)
{
if(l >= r) return;
int mid = (l + r) >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid+1, r);
int k = 0, i = l, j = mid + 1;
while(i<=mid && j<=r)
{
if(q[i] <= q[j]) tmp[++k] = q[i++];
else
{
tmp[++k] = q[j++];
ans += mid + 1 - i; //计算逆序对的数量
}
}
while(i <= mid) tmp[++k] = q[i++];
while(j <= r) tmp[++k] = q[j++];
for(i=l, j=1; i<=r; i++) q[i] = tmp[j++];
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
merge_sort(a, 1, n);
printf("%lld", ans);
return 0;
}
快速幂取模
前置推导
处理形如\(a^b\ \%\ c\ =\ ?\)的问题
前置知识:
公式一:
\((a*b)\%c == ((a\%c)*(b\%c))\%c\)
\((a*b)\%c ==((a\%c)*b)\%c\)
公式二:
\(a^b\%c == (a\%c)^b\%c\)
注:公式二可由公式一推导得出
\((a^b)\%c == (a*a*a...)\%c\)
\(==((a\%c)*(a\%c)*(a\%c)...)\%c\)
\(==((a\%c)^b)\%c\)
算法1:
int ans = 1;
for(int i=1; i<=b; i++)
{
ans = ans * a;
}
ans = ans % c;
时间复杂度:\(O(b)\)
问题:如果\(a\)和\(b\)过大,很容易就会溢出
算法2:
根据公式二优化:
int ans = 1;
a = a % c; //缩小a的值
for(int i=1; i<=b; i++)
{
ans = ans * a;
}
ans = ans % c;
算法3:
既然相乘再取余与取余再相乘保持余数不变,那么新算法得的ans也可以进行取余,在算法2的基础上进行改进
int ans = 1;
a = a % c; //缩小a的值
for(int i=1; i<=b; i++)
{
ans = (ans * a) % c;
}
ans = ans % c;
时间复杂度:\(O(b)\)
问题:如果\(b\)过大,可能超时
算法4:
根据公式二优化,考虑\(b\)的奇偶性
1、b为偶数
\(a^b\%c == ((a^2)^{b/2})\%c == ((a^2\%c)^{b/2})\%c\)
2、b为奇数
\(a^b\%c == (a*(a^2)^{b/2})\%c == (a*(a^2\%c)^{b/2})\%c\)
令\(k=a^2\%c\),那么
\(b\)为偶数:求\(k^{b/2}\%c\)即可
\(b\)为奇数:求\((a*k^{b/2}\%c)\%c\)即可
int ans = 1;
a = a % c; //缩小a的值
//如果b为奇数,要多求一步,可以提前算到ans中
if(b % 2 == 1) ans = (ans * a) % c;
k = (a * a) % c;
for(int i=1; i<=b/2; i++)
{
ans = (ans * k) % c;
}
ans = ans % c;
时间复杂度:\(O(b/2)\)
问题:如果\(b\)过大,依然可能超时
算法5:
通过算法4,直接将时间复杂度由\(O(b)\)优化到\(O(b/2)\)。
当令\(k=(a*a)\%c\)时,所求的结果变为了\(k^{b/2}\%c\);
此时令\(a=k,b=b/2\),则又变成了求\(a^{b}\%c\),但此时的b相对于最初已经缩小了一半,而这个过程可以迭代下去。
当\(b==0\)时,所有的因子都已经相乘,算法结束。
于是便可以在\(O(logb)\)的时间内完成了,便有了最终算法
int ans = 1;
a = a % c; //缩小a的值
while(b > 0)
{
if(b % 2 == 1) ans = (ans * a) % c;
b = b / 2;
a = (a * a) % c;
}
蒙哥马利算法
蒙哥马利快速幂取模算法,简单漂亮
有彼得·蒙德马利在1985年提出
//求a^b%c
int Montgomery(int a, int b, int c)
{
int ans = 1;
a = a % c;
while(b > 0)
{
//位运算
//b&1==1表示b为奇数,为0表示为偶数
if(b & 1) ans = (ans * a) % c; //奇数,补一项
b = b >> 1;
a = (a * a) % c;
}
return ans;
}
例题
PJ219 取余运算
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll montgomery(ll a, ll b, ll c)
{
ll ans = 1;
a = a % c;
while(b > 0)
{
if(b & 1) ans = (ans * a) % c;
b = b >> 1;
a = a * a % c;
}
return ans;
}
int main()
{
ll a = 0, b = 0, c = 0;
scanf("%lld%lld%lld", &a, &b, &c);
printf("%lld^%lld mod %lld=%lld", a, b, c, montgomery(a, b, c));
return 0;
}
贪心算法
优先队列
特性
1、普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。
2、优先队列具有队列的所有特性,包括队列的基本操作,只是在这基础上添加了内部的一个排序,它本质是一个堆实现的。
3、在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。
4、优先队列具有最高级先出的行为特征
基本操作
定义:
原型: priority_queue<Type,Container,Functional>
Type:数据类型
Container:容器类型(STL里面默认用的是vector)
Functional:比较的方式
当需要用自定义的数据类型时才需要传入这三个参数,使用基本数据类型时,只需要传入数据类型,默认是大根堆
//大根堆
priority_queue<int> q1;
//大根堆,与上面的q1等价
priority_queue<int, vector<int>, less<int>> q2;
//小根堆
priority_queue<int, vector<int>, greater<int>> q3;
支持的操作:
- top 访问队头元素,此时优先队列不能为空(\(O(1)\))
- empty 队列是否为空(\(O(1)\))
- size 返回队列内元素个数(\(O(1)\))
- push 插入元素到队尾(\(O(logn)\))
- pop 弹出队头元素,此时优先队列不能为空(\(O(logn)\))
- swap 交换内容
- emplace 原地构造一个元素并插入队列
基本类型的优先队列
#include<bits/stdc++.h>
using namespace std;
//大根堆
priority_queue<int> q1;
//小根堆
priority_queue<int, vector<int>, greater<int>> q2;
priority_queue<string> q3;
int main()
{
for(int i=1; i<=5; i++)
{
q1.push(i);
q2.push(i);
}
//该循环输出5 4 3 2 1
while(!q1.empty())
{
printf("%d ", q1.top());
q1.pop();
}
printf("\n");
//该循环输出1 2 3 4 5
while(!q2.empty())
{
printf("%d ", q2.top());
q2.pop();
}
printf("\n");
q3.push("abc");
q3.push("abcd");
q3.push("cbd");
//该循环输出cbd abcd abc
while(!q3.empty())
{
cout << q3.top() << " ";
q3.pop();
}
printf("\n");
return 0;
}
pair类型的优先队列
#include<bits/stdc++.h>
using namespace std;
//最后一个>前往往要加个空格
//防止编辑器认为是>>
priority_queue<pair<int, int> > q1;
int main()
{
q1.push(make_pair(1, 2));
q1.push(make_pair(1, 3));
q1.push(make_pair(2, 5));
while(!q1.empty())
{
printf("%d %d\n", q1.top().first, q1.top().second);
q1.pop();
}
//输出:
//2 5
//1 3
//1 2
return 0;
}
自定义类型的优先队列
自定义类型的优先级是基于小于号比较的,所以只需要重载小于号即可。
#include<bits/stdc++.h>
using namespace std;
struct student
{
int age; //年龄
string name; //姓名
//年龄由小到大,如果年龄相同,则按姓名字典序由大到小
bool operator < (const student &stu) const
{
if(age == stu.age) return name > stu.name;
return age < stu.age;
}
};
priority_queue<student> q1;
int main()
{
q1.push({15, "zhangsan"});
q1.push({15, "lisi"});
q1.push({16, "wangwu"});
while(!q1.empty())
{
cout << q1.top().age << " " << q1.top().name << endl;
q1.pop();
}
//输出:
//16 wangwu
//15 lisi
//15 zhangsan
return 0;
}
自定义数据数据类型的一个小技巧:优先队列默认是维护大根堆,但我们可以通过重载<号的规则,达到我们想要的结果
#include<bits/stdc++.h>
using namespace std;
struct student
{
int age; //年龄
string name; //姓名
//这里重载<
bool operator < (const student &stu) const
{
//如果写成age < stu.age,则年龄大的优先级高
//如果写成age > stu.age,则年龄小的优先级高
return age > stu.age;
}
};
priority_queue<student> q1;
int main()
{
q1.push({15, "lisi"});
q1.push({14, "zhangsan"});
q1.push({16, "wangwu"});
while(!q1.empty())
{
cout << q1.top().age << " " << q1.top().name << endl;
q1.pop();
}
return 0;
}
基础贪心
理论基础
引入:
贪心算法是用计算机来模拟一个贪心的人做出决策的过程。这个人十分贪婪,每一步行动总是按某种指标选取最优的操作。而且他目光短浅,总是只看眼前,并不考虑以后可能造成的影响。
因此,并不是所有的时候贪心法都能获得最优解,所以一般使用贪心法的时候,都要确保自己能证明其正确性。
适用范围:
贪心算法在有最优子结构的问题中尤为有效。
最优子结构的意思是问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
证明:
贪心算法有两种证明方法:反证法和归纳法。一般情况下,一道题只会用到其中的一种方法来证明。
1、反证法:如果交换方案中任意两个元素/相邻的两个元素后,答案不会变的更好,那么可以推定目前的解已经是最优解了。
2、归纳法:先算得出边界情况(例如\(n=1\))的最优解\(F_1\),然后再证明:对于每个\(n\),\(F_{n+1}\)都可以由\(f_n\)推导出结果。
例题
合并果子
#include<bits/stdc++.h>
using namespace std;
/*
贪心策略:
先合并小的,再合并大的
*/
int n = 0;
priority_queue<int, vector<int>, greater<int>> q;
int main()
{
int x = 0, ans = 0;
int a = 0, b = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &x);
q.push(x);
}
while(q.size() >= 2)
{
a = q.top();
q.pop();
b = q.top();
q.pop();
ans += a + b;
q.push(a+b);
}
printf("%d\n", ans);
return 0;
}
纪念品分组
贪心策略: 判断价格最大的物品和价格最小的物品价格的和是否超过了w,如果超过了,则价格最大物品单独一组,没超过则价格最大和最小一组
合理性证明:
1、思考:价值最大的物品有没有必要再跟价格第二小和价格第三小或之前的再组合
2、没必要
3、比如\(p_1<p_2<p_3<p_4<p_5\),如果\(p_5\)与\(p_2\)组合为一组,那么\(p_1\)和\(p_2\)都可以和其他任何物品组合为一组,即选\(p_1\)和\(p_2\)都一样
#include<bits/stdc++.h>
using namespace std;
int w = 0, n = 0;
int a[30010] = {};
int ans = 0;
//先对数组从小到大排序,如果最大+最小<=w,则分一组,否则最大单独一组
int main()
{
scanf("%d%d", &w, &n);
for(int i=1; i<=n; i++) scanf("%d", &a[i]);
sort(a+1, a+1+n);
int l=1, r = n;
while(l<=r)
{
if(a[r]+a[l] <= w) l++;
r--;
ans++;
}
printf("%d", ans);
return 0;
}
反悔贪心
思想
思路是无论当前的选项是否最优都接受,然后进行比较,如果选择之后不是最优了,则反悔,舍弃掉这个选项;否则,正式接受。如此往复。
例题
[Usaco2009 Open]工作安排Job
思路:
1、将任务按截止时间由小到大进行排序,先做截止时间靠前的任务,这样可以保证尽量多做任务
2、用小根堆维护已做的所有任务,\(q.top\)就是已做的任务中,最小利润;\(q.size\)就是已做任务的数量
2、当遍历到第\(i\)个任务时,假如该任务截止时间为\(ndlist[i].d\)
3、如果当前已做的任务量\(q.size<ndlist[i].d\),说明这个任务直接就可以做
4、【反悔】如果任务量\(q.size>=ndlist[i].d\),那么就要把之前所做的所有任务中,利润最小的任务删掉,换成第\(i\)个任务,这样可以使总利润最大
#include<bits/stdc++.h>
using namespace std;
int n = 0;
struct Node
{
int d, p;
}ndlist[100010];
//q表示当前利润最小的工作
priority_queue<int, vector<int>, greater<int>> q;
long long ans = 0;
bool cmp(Node &nd1, Node &nd2)
{
return nd1.d < nd2.d;
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d%d", &ndlist[i].d, &ndlist[i].p);
}
sort(ndlist+1, ndlist+1+n, cmp);
for(int i=1; i<=n; i++)
{
//如果当前工作截止日期>所做工作总的数量
//说明直接做这件事就可以
if(ndlist[i].d > q.size())
{
q.push(ndlist[i].p);
ans += ndlist[i].p;
}
else
{
//找到这个截止日期前利润最小的工作
//如果当前工作利润大,则把利润最小的工作删去
if(ndlist[i].p > q.top())
{
ans += ndlist[i].p - q.top();
q.pop();
q.push(ndlist[i].p);
}
}
}
printf("%lld", ans);
return 0;
}
树基础
引入
图论中的树和现实生活中的树长得一样,只不过我们习惯于处理问题的时候把树根放到上方来考虑。这种数据结构看起来像是一个倒挂的树,因此得名。
一些概念
树的概念:
1、树是一种常见的非线性的数据结构
2、树是\(n(n>0)\)个节点的有限集合,这个集合满足一下条件:
①有且仅有一个节点没有前驱(父亲节点),该节点称为树的根
②除根外,其余的每个结点都有且仅有一个父节点
③除根外,每一个节点都通过唯一的路径连到根上。这条路径由根开始,而末端就在该节点上,且除根以外,路径上的每一个结点都是前一个结点的后驱(儿子节点)
父亲: 对于除根以外的每个结点,定义为从该结点到根路径上的第二个结点。根结点没有父结点。
祖先: 一个结点到根结点的路径上,除了它本身外的结点。根结点的祖先集合为空。
根结点: 没有前驱的结点。在树中有且仅有一个根结点。根结点到每一个结点的路径是唯一的
叶节点: 没有后驱的结点称为树叶。由树的定义可知,树叶本身也是其父结点的子树。
子结点: 如果\(u\)是\(v\)的父亲,那么\(v\)是\(u\)的子结点。子结点的顺序一般不加以区分,二叉树是一个例外。
结点的度: 一个结点的子树数目称为该结点的度
树的度: 所有结点中最大的度称为该树的度
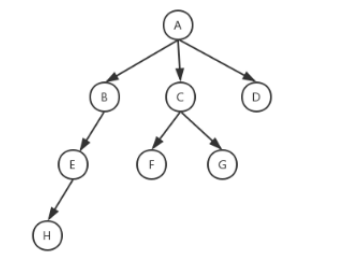
上图中,A结点的度为3,B结点的度为1,C结点的度为2,等等。树的度为3
结点的深度: 到根结点的路径上的边数
树的深度(高度): 所有节点的深度的最大值

上图中,A的深度为0,BCD的深度为1,EFG的深度为2,H的深度为3。树的深度为3
兄弟: 同一个父亲的多个子结点互为兄弟
后代: 子结点和子结点的后代
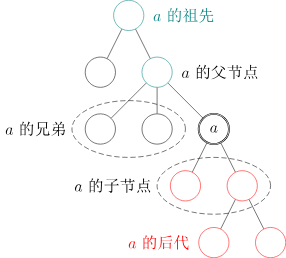
子树: 删掉与父亲相连的边后,该结点所在的子图。

特殊的树:
链: 满足与任一结点相连的边不超过\(2\)条的树称为链
菊花/星星: 满足存在u使得所有除u以外节点均与u相连的数称为菊花
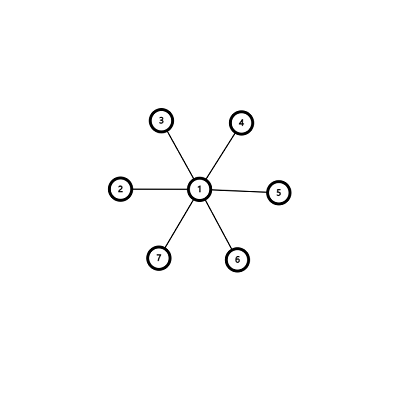
森林: 树的集合称为森林。树和森林之间有着密切的关系。删除一个树的根结点,其所有原来的子树都是树,构成森林。用一个结点连接到森林的所有树的根结点就构成树。
树的存储
方法1:数组,称为“父亲表示法”
const int maxn = 10; //树的结点数
struct node
{
int data, parent; //数据域,指针域
};
node tree[maxn];
优缺点:利用了树中除根结点外每个结点都有唯一的父结点这个性质。很容易找到树根,但找孩子时需要遍历整个线性表。
方法2:树型单链表结构,称为“孩子表示法”
每个结点包括一个数据域和一个指针域(指向若干子结点)。称为“孩子表示法”。假设树的度为10,树的结点仅存放字符,则这棵树的数据结构定义如下:
const int maxn = 210; //最多节点数
const int maxm = 10; //树的度
struct node
{
char data; //数据域
int child[maxm]; //指针域,指向若干孩子结点,值对应的是tree数组的下标
};
node tree[maxn];
缺陷:只能从根(父)结点遍历到子结点,不能从某个子结点返回到它的父结点。但程序中确实需要从某个结点返回到它的父结点时,就需要在结点中多定义一个指针变量存放其父结点的信息。这种结构又叫带逆序的树型结构。
方法3:树型双链表结构,称为“父亲孩子表示法”
每个结点包括一个数据域和二个指针域(一个指向若干子结点,一个指向父结点)。假设树的度为10,树的结点仅存放字符,则这棵树的数据结构定义如下:
const int maxn = 210; //最多节点数
const int maxm = 10; //树的度
struct node
{
char data; //数据域
int child[maxm]; //指针域,指向若干孩子结点,值对应的是tree数组的下标
int father; //指向父亲
};
node tree[maxn];
方法4:二叉树型表示法,称为“孩子兄弟表示法”
也是一种双链表结构,但每个结点包括一个数据域和二个指针域(一个指向该结点的第一个孩子结点,一个指向该结点的下一个兄弟结点)。称为“孩子兄弟表示法”。
const int maxn = 210; //最多节点数
struct node
{
char data; //数据域
int firstchild, next; //指针域,分别指向第一个孩子结点和下一个兄弟结点
};
node tree[maxn];
例题:找树根和孩子
#include <bits/stdc++.h>
using namespace std;
int n = 0, m = 0;
//flag=false表示节点不存在,flag=true表示节点存在
//parent[i]表示节点i的父亲节点
//child[i]表示节点i的儿子的数量
int parent[110] = {}, child[110] = {}, flag[110] = {};
int main()
{
int x = 0, y = 0;
scanf("%d%d", &n, &m);
for(int i=1; i<=m; i++)
{
scanf("%d%d", &x, &y);
flag[x] = flag[y] = 1;
parent[y] = x;
child[x]++;
}
//找树根
for(int i=1; i<=n; i++)
{
if(flag[i] && parent[i] == 0)
{
printf("%d\n", i);
break;
}
}
//找孩子最多的节点
int maxx = 0, t = 0;
for(int i=1; i<=n; i++)
{
if(t < child[i])
{
t = child[i];
maxx = i;
}
}
printf("%d\n", maxx);
//输出maxx的孩子
for(int i=1; i<=n; i++)
{
if(parent[i] == maxx) printf("%d ", i);
}
return 0;
}
二叉树
概念
1、二叉树是一种很重要的非线性数据结构,它的特点是每个结点最多有两个后继,且其子树有左右之分(次序不能任意颠倒)
2、二叉树是以结点为元素的有限集,它或者为空,或者满足以下条件:
- 有一个特定的结点为根
- 余下的结点分为互不相交的子集\(L\)和\(R\),其中\(L\)是根的左子树;\(R\)是根的右子树;\(L\)和\(R\)又是二叉树
3、由上述定义可以看出,二叉树和树是两个不同的概念
- 树的每一个结点可以有任意多个后继,而二叉树中的每个节点的后继不能超过2
- 树的子树可以不分次序(除有序树外);而二叉树的子树有左右之分。我们称二叉树中结点的左后继为左儿子,右后继为右儿子
性质
1、在二叉树的第\(i\)层上最多有\(2^{i-1}\)个节点。(\(i>=1\))
证明:画个图就明白了
2、二叉树中如果深度为\(k\),那么最多有\(2^{k}-1\)个节点
证明:总结点数=\(2^0+2^1+2^2+···+2^{k-1}\),根据等比数列求和公式,得出总数=\(2^{k}-1\)
3、\(n_0=n_2+1\),\(n_0\)表示度为\(0\)的节点数,\(n_2\)表示度为\(2\)的节点数
证明
n表示总结点数量
①\(n=n_0+n_1+n_2\),即总结点数为度为\(0\)和度为\(1\)和度为\(2\)的节点的和
②\(n=2*n_2+n_1+1\),即度为\(2\)的结点有两个子结点,度为\(1\)的结点有\(1\)个子结点,再加上根节点,也是节点总数
上述两个结合,即可推出\(n_0=n_2+1\)
4、在完全二叉树中,具有\(n\)个节点的完全二叉树的深度为\(\lfloor \log_2 n \rfloor + 1\)
证明
步骤1:明确完全二叉树的深度与节点数范围
设完全二叉树的深度为\(k\)(注:深度定义为“根节点所在层为第1层”)。
完全二叉树的核心特点:前\(k-1\)层是满二叉树,第\(k\)层(最后一层)的节点从左到右连续排列。
因此,深度为\(k\)的完全二叉树,节点数\(n\)的范围是:
- 最少节点数:前\(k-1\)层是满二叉树(节点数为\(2^{k-1} - 1\)),第\(k\)层至少有1个节点,故\(n \geq 2^{k-1}\)。
- 最多节点数:前\(k\)层是满二叉树(节点数为\(2^k - 1\)),故\(n \leq 2^k - 1\)。
综上,节点数范围可表示为:
\(2^{k-1} \leq n \leq 2^k - 1\)
步骤2:对节点数范围取对数
由于对数函数\(\log_2 x\)是单调递增函数,对不等式\(2^{k-1} \leq n \leq 2^k - 1\)取以2为底的对数:
\(\log_2 2^{k-1} \leq \log_2 n \leq \log_2 (2^k - 1)\)
化简得:
\(k-1 \leq \log_2 n < k\)
(注:因\(2^k - 1 < 2^k\),故\(\log_2 (2^k - 1) < \log_2 2^k = k\))
步骤3:结合向下取整的定义推导深度
根据向下取整(\(\lfloor x \rfloor\)) 的定义:\(\lfloor x \rfloor\)是“不大于\(x\)的最大整数”。
由\(k-1 \leq \log_2 n < k\)可知:
\(\lfloor \log_2 n \rfloor = k-1\)
两边加1后得到:
\(k = \lfloor \log_2 n \rfloor + 1\)
综上,具有\(n\)个节点的完全二叉树的深度为\(\lfloor \log_2 n \rfloor + 1\)。
5、若对含\(n\)个结点的完全二叉树从上到下且从左至右进行\(1\)至\(n\)的编号,则对完全二叉树中任意一个编号为\(i\)的结点有如下特性:
- 若\(i=1\),则该结点是二叉树的根,无双亲, 否则,编号为\([i/2]\)的结点为其双亲结点;
- 若\(2*i>n\),则该结点无左孩子, 否则,编号为\(2*i\)的结点为其左孩子结点;
- 若\(2*i+1>n\),则该结点无右孩子结点, 否则,编号为\(2*i+1\)的结点为其右孩子结点。
类型
二叉树: 每个结点最多只有两个儿子(子结点)的有根树称为二叉树。
常常对两个子结点的顺序加以区分,分别称之为左子结点和右子节点。
大多数情况下,二叉树一词均指有根二叉树。
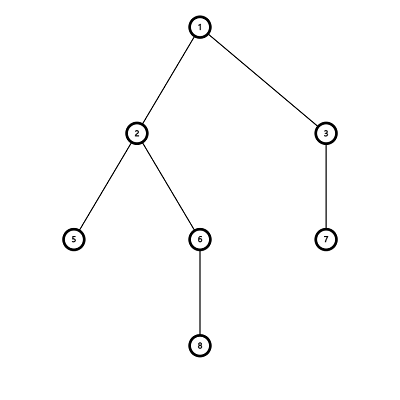
完整二叉树: 每个结点的子结点数量均为0或者2的二叉树。换言之,每个结点或者是树叶,或者左右子树均非空
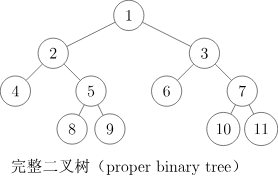
完全二叉树: 只有最下面两层结点的度数可以小于2,且最下面一层的结点都集中在该层最左边的连续位置上。
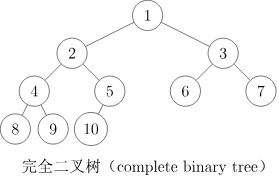
完美二叉树: 所有叶节点的深度均相同,且所有非叶节点的子节点数量均为2的二叉树称为完美二叉树
\(OIers\)所说的满二叉树多指完美二叉树
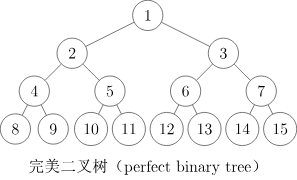
二叉树的存储结构
将每个结点依次存放在一维数组中,用数组下标指示结点编号,编号的方法是从根结点开始编号1,然后由左而右进行连续编号。每个结点的信息包括
- 一个数据域(data)
- 两个指针域,左儿子结点编号(lch)和右儿子结点编号(rch)
const int maxn = 30;
struct node
{
char data;
int lch, rch;
}tr[maxn];
二叉树的遍历
在应用树结构解决问题时,往往要求按照某种次序获得树中全部节点的信息,这种操作叫做树的遍历。
先序(根)遍历
思想: 先访问根节点,再从左到右按照先序思想遍历各棵子树。

中序(根)遍历
思想: 先遍历左子树,再访问根节点,最后遍历右子树

后序(根)遍历
思想: 先遍历左子树,再遍历右子树,最后访问根节点

反推
已知中序遍历序列和另外一个序列可以求第三个序列
推理:
1、前序的第一个是root,后序的最后一个是root
2、先确定根节点,然后根据中序遍历,在根左边的为左子树,根右边的为右子树
3、对于每一个子树可以看成一个全新的树,仍然遵循上面的规律

层序遍历
树层序遍历是指按照从根节点到叶子结点的层次关系,一层一层的横向遍历各个节点。根据BFS的定义可以知道,BFS所得到的遍历顺序就是一种层序遍历。但层序遍历要求将不同的层次区分开来,所以其结果通常以二维数组的形式表示。
例如:下图的树的层序遍历的结果是[[1],[2,3,4],[5,6]]

例题
二叉树的遍历
#include <bits/stdc++.h>
using namespace std;
const int maxn = 30;
struct node
{
char data;
int lch, rch;
}tr[maxn] = {};
int n = 0;
//前序遍历
void preorder(int rt)
{
printf("%c", tr[rt].data);
if(tr[rt].lch) preorder(tr[rt].lch);
if(tr[rt].rch) preorder(tr[rt].rch);
}
//中序遍历
void inorder(int rt)
{
if(tr[rt].lch) inorder(tr[rt].lch);
printf("%c", tr[rt].data);
if(tr[rt].rch) inorder(tr[rt].rch);
}
//后序遍历
void postorder(int rt)
{
if(tr[rt].lch) postorder(tr[rt].lch);
if(tr[rt].rch) postorder(tr[rt].rch);
printf("%c", tr[rt].data);
}
int main()
{
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf(" %c%d%d", &tr[i].data, &tr[i].lch, &tr[i].rch);
}
//输出前序遍历
preorder(1);
printf("\n");
//输出中序遍历
inorder(1);
printf("\n");
//输出后序遍历
postorder(1);
return 0;
}
求后序遍历
#include <bits/stdc++.h>
using namespace std;
string a, b;
//s1先序遍历,s2中序遍历,输出后续遍历
void work(string s1, string s2)
{
int len = s1.size();
if(len == 1)
{
cout << s1[0];
return;
}
//求根在中序遍历中的位置
int k = s2.find(s1[0]);
string s3, s4;
if(k > 0) //如果位置大于0,表明有左子树
{
s3 = s1.substr(1, k); //左子树的前序遍历
s4 = s2.substr(0, k); //左子树的中序遍历
work(s3, s4);
}
if(k < len - 1) //如果位置小于最后一个字符的下标表明有右子树
{
s3 = s1.substr(k+1, len-k-1); //右子树的前序遍历
s4 = s2.substr(k+1, len-k-1); //右子树的中序遍历
work(s3, s4);
}
cout << s1[0];
}
int main()
{
cin >> a >> b;
work(a, b);
return 0;
}
普通树转二叉树
普通有序树转换成二叉树
普通树为有序树T,将其转化成二叉树T’的规则如下:
- T中的结点与T’中的结点一一对应,即T中每个结点的序号和值在T’中保持不变;
- T中某结点v的第一个儿子结点为v1,则在T’中v1为对应结点v的左儿子结点;
- T中结点v的儿子序列,在T’中被依次链接成一条开始于v1的右链;

普通树转换成二叉树
- 将树的根节点直接作为二叉树的根节点
- 将树的根节点的第一个子节点作为根节点的左儿子,若该子节点存在兄弟节点,则将该子节点的第一个兄弟节点(方向从左往右)作为该子节点的右儿子
- 将树中的剩余节点按照上一步的方式,依序添加到二叉树中,直到树中所有的节点都在二叉树中

二叉树怎样还原为树
- 逆操作,把所有的右孩子变为兄弟

森林转换成二叉树
方法
如果\(m\)棵互不相交的普遍有序树组成了森林\(F={T_1,…T_m}\)。我们可以按下述规则将森林\(F\)转换成一棵二叉树\(b={R,L_B,R_B}\):
- 若\(F\)为空(\(m=0\)),则\(b\)为空树;
- 若\(F\)非空(\(m≠0\))
- 则\(b\)的根\(R\)即为森林中第一棵树的根\(R(T_1)\);
- \(b\)的左子树\(L_B\)是从\(T1\)的根结点的子树森林\(F_1={T1_1,T1_2,…T1_k}\)转换而成的二叉树;
- 其右子树\(R_B\)是从森林\(F_2={T_2,T_3,…,T_m}\)转换成的二叉树。

步骤
将森林转换为二叉树的步骤是:
1.先把每棵树转换为二叉树;
2.第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子结点,用线连接起来。当所有的二叉树连接起来后得到的二叉树就是由森林转换得到的二叉树。

例题
普通树转二叉树
#include <bits/stdc++.h>
using namespace std;
const int maxn = 30;
struct node
{
char data;
int lch, rch;
}tr[maxn] = {};
int n = 0;
//前序遍历
void preorder(int rt)
{
printf("%c", tr[rt].data);
if(tr[rt].lch) preorder(tr[rt].lch);
if(tr[rt].rch) preorder(tr[rt].rch);
}
//中序遍历
void inorder(int rt)
{
if(tr[rt].lch) inorder(tr[rt].lch);
printf("%c", tr[rt].data);
if(tr[rt].rch) inorder(tr[rt].rch);
}
//后序遍历
void postorder(int rt)
{
if(tr[rt].lch) postorder(tr[rt].lch);
if(tr[rt].rch) postorder(tr[rt].rch);
printf("%c", tr[rt].data);
}
int main()
{
int x = 0, y = 0;
//要将普通树转为二叉树
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf(" %c", &tr[i].data);
//第一个叶子节点作为左子树
scanf("%d", &x);
if(x == 0) continue;
tr[i].lch = x;
//剩下的叶子节点依次链接为右链
y = x;
while(1)
{
scanf("%d", &x);
if(x == 0) break;
tr[y].rch = x;
y = x;
}
}
//输出前序遍历
preorder(1);
printf("\n");
//输出后序遍历
postorder(1);
return 0;
}
二叉排序树
概念
定义: 二叉排序树又称二叉查找树、二叉搜索树。它或者是一棵空树;或者是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 左、右子树也分别为二叉排序树
特点: 只要按中序遍历即可得到由小到大的有序序列
![013]()
中序遍历:2,3,4,8,9,9,10,13,15,18,21
二叉排序树的建立(逐点插入法)
设\(K=\{k_1,K_2,k_3,......,k_n\}\)为具有\(n\)个数据元素的序列。从序列的第一个元素开始,依次取序列中的元素,每取一个元素\(k_i\),按照下述原则将\(k_i\)插入到二叉树中:
- 若二叉树为空,则\(k_i\)作为该二叉树的根节点
- 若二叉树非空,则将\(k_i\)与该二叉树的根节点的值比较
- 若\(k_i\)小于根节点的值,则将\(k_i\)插入到根节点的左子树中
- 否则,将\(k_i\)插入到根节点的右子树中
将\(k_i\)插入到左子树或者右子树中仍然遵循上述原则
![014]()
二叉排序树的查找
由二叉树的递归定义性质,二叉排序树的查找同样可以使用如下递归算法查找
- 若二叉排序树为空,则查找失败,查找结束
- 若二叉排序树非空,则将查找元素与二叉排序树的根节点的值进行比较
- 若等于根节点的值,则查找成功,返回根节点的值
- 若小于根节点的值,则在根节点的左子树查找
- 若大于根节点的值,则在根节点的右子树查找
直到查找成功或者失败
在理想情况下,每次比较过后,树会被砍掉一半,近乎折半查找。
二叉排序树的插入
二叉排序的插入是建立在二叉排序的查找之上的,插入一个结点,就是通过查找发现该结点合适插入位置,把结点直接放进去。 其实构造二叉排序树的过程中就是结点插入过程。由此可以得出二叉排序树插入规则如下:
- 若二叉树是空树,则将p所指结点作为根结点插入
- 若查找的key已经在树中,则p指向该结点右子树或其他操作(如何操作根据题意)。
- 若查找的key没有在树中,则p指向查找路径上最后一个结点。
例如:若在图2.6展示的二叉排序树中插入结点数据为60的结点。
首先查找结点数据为60的结点,二叉排序树中不存在结点为60的结点,因此查找失败。此时查找指针p指向查找路径最后一个结点即指向59结点。由于60>59且59结点右子树为空,故将60结点作为59结点的右孩子,插入完成。插入后的二叉排序树如图2.8所示。


二叉排序树的删除
二叉树的删除可不再像二叉树的插入那么容易了,因为删除某个结点以后,会影响到树的其它部分的结构。
删除的时候需要考虑以下几种情况:
- 删除结点为叶子结点
- 删除的结点只有左子树
- 删除的结点只有右子树
- 删除的结点既有左子树又有右子树
考虑前三种情况,处理方式比较简单。
例如:若要删除图2.8中的结点93,则直接删除该结点即可。删除后二叉排序树如图2.9所示:


若要删除的结点为结点35,结点35只有右子树,只需删除结点35,将右子树37结点替代结点35即可。删除后的二叉排序树如图2.10所示:


删除只有左子树的结点与此情况类似。
情况4相对比较复杂,对于待删除结点既有左子树又有右子树的情形,最佳办法是在剩余的序列中找到最为接近的结点来代替删除结点。这种代替并不会影响到树的整体结构。那么最为接近的结点如何获取呢?
可以采用中序遍历的方式来得到删除结点的前驱和后继结点。选取前驱结点或者后继结点代替删除结点即可。
例如:待删除的结点为47,图2.8中二叉排序树的中序遍历序列为35 37 47 51 59 60 61 73 87 93 98。则结点47的前驱结点为37,则直接将37结点替代47结点即可。替换后的二叉排序树如图2.11所示:


例题
二叉排序树
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x7fffffff;
struct node
{
int data, lson, rson;
node() { data = inf; }
}tr[maxn];
int n = 0, tot = 0, root = 0;
//中序遍历
void inorder(int rt)
{
if(tr[rt].lson) inorder(tr[rt].lson);
printf("%d ", tr[rt].data);
if(tr[rt].rson) inorder(tr[rt].rson);
}
//后序遍历
void postorder(int rt)
{
if(tr[rt].lson) postorder(tr[rt].lson);
if(tr[rt].rson) postorder(tr[rt].rson);
printf("%d ", tr[rt].data);
}
void insertnd(int &rt, int x)
{
//代表该点还未赋值
if(rt == 0)
{
rt = ++tot;
tr[rt].data = x;
return;
}
if(x < tr[rt].data) insertnd(tr[rt].lson, x);
else insertnd(tr[rt].rson, x);
}
int main()
{
int x = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++)
{
scanf("%d", &x);
insertnd(root, x);
}
inorder(root);
printf("\n");
postorder(root);
return 0;
}
最优二叉树
概念
路径和路径长度
路径: 在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路。
路径长度: 通路中分支的数目称为路径长度。
若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。

图2.1所示二叉树结点\(A\)到结点\(D\)的路径长度为\(2\),结点\(A\)到达结点\(C\)的路径长度为\(1\)。
结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度:从根结点到该结点之间的路径长度与该结点的权的乘积。
图2.2展示了一棵带权的二叉树

树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为\(WPL\)。
图2.2所示二叉树的\(WPL\):
\(WPL = 6 * 2 + 3 * 2 + 8 * 2 = 34\)

最优二叉树(霍夫曼树)
给定\(n\)个权值作为\(n\)个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为霍夫曼树(Huffman Tree)。
如图3.1所示两棵二叉树

叶子结点为\(A、B、C、D\),对应权值分别为\(7、5、2、4\)
3.1.a树的WPL = 7 * 2 + 5 * 2 + 2 * 2 + 4 * 2 = 36
3.1.b树的WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3 = 35
由\(ABCD\)构成叶子结点的二叉树形态有许多种,但是\(WPL\)最小的树只有3.1.b所示的形态。则3.1.b树为一棵霍夫曼树。
构造最优二叉树
假定给出\(n\)个结点\(k_i(i=1‥n)\),其权值分别为\(W_i(i=1‥n)\)。要构造以此\(n\)个结点为叶结点的最优二叉树,其构造方法如下:
将给定的\(n\)个结点构成\(n\)棵二叉树的集合\(F={T_1,T_2,……,T_n}\)。其中每棵二叉树\(T_i\)中只有一个权值为\(w_i\)的根结点\(k_i\),其左、右子树均为空。然后做以下两步
- 在\(F\)中选取根结点权值最小的两棵二叉树作为左右子树,构造一棵新的二叉树,并且置新的二叉树的根结点的权值为其左、右子树根结点的权值之和
- 在\(F\)中删除这两棵二叉树,同时将新得到的二叉树加入\(F\)重复⑴、⑵,直到在\(F\)中只含有一棵二叉树为止。这棵二叉树便是最优二叉树
在森林中选取两棵根结点权值最小的树作左右子树,构造一棵新的二叉树,置新二叉树根结点权值为其左右子树根结点权值之和;
在森林中删除这两棵树,同时将新得到的二叉树加入森林中;
重复上述两步,直到只含一棵树为止,这棵树即霍夫曼树。

霍夫曼树性质
1、初始森林中的\(n\)棵二叉树,每棵树有一个孤立的结点,它们既是根,又是叶子
2、\(n\)个叶子的哈夫曼树要经过\(n-1\)次合并,产生\(n-1\)个新结点。最终求得的哈夫曼树中共有\(2n-1\)个结点
3、哈夫曼树是严格的二叉树,没有度数为\(1\)的分支结点
4、最优二叉树构造过程中运用到了贪心思想




 浙公网安备 33010602011771号
浙公网安备 33010602011771号