20251222 - 强连通分量

20251222 - 强连通分量

前言：

Tarjan 爷爷太巨了！！！

DFS 生成树（OI-WIKI的）

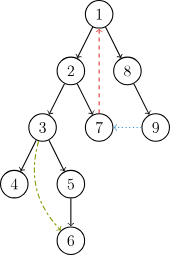
在有向图中，DFS生成树有4种边：

1. 树边，黑色实线，从父节点指向还没有被访问的子节点。

2. 返祖边，红色虚线，指向祖先节点的边。

3. 前向边，绿色虚线，指向子树中的边。（没啥用）

4. 横叉边，蓝色虚线，指向已经访问过的，不是祖先节点也不是子树中的边。

SCC（强连通分量）

有向图中，如果一个图满足任意两点之间都可达，那么我们就称它是强连通的。

可以定义 \(low_u\) 为 \(u\) 号点可以到的最小时间戳（DFN），可以发现，如果 \(low_u = dfn_u\)，就可以构成一个强连通分量，因为他无法再向上走了。

但是有一个问题，如果有没有用的横叉边不就凉凉了，\(low_u\) 会不知道更新到哪去！

如果 \(u\) 存在于 SCC 中，当且仅当这个点访问过并在栈中，这样的才有用。

所以代码很好写：

inline void Tarjan(int u) { // inline 有什么作用呢？？？
  dfn[u] = low[u] = ++idx; 
  stk[++top] = u; // 手写栈
  ins[u] = 1; // 是否在栈中
  for (auto v : edges[u]) {
    if (!dfn[v]) {
      Tarjan(v);
      low[u] = min(low[u], low[v]);
    }else if (ins[v]){
      low[u] = min(low[u], dfn[v]); // 为什么是 dfn[v] 呢？
    } // 因为它只能走一条返祖边！！！
  }
  if (low[u] == dfn[u]) {
    vector <int> ve;
    while (1) {
      int v = stk[top--];
      ins[v] = 0;
      ve.push_back(v);
      if (v == u) break; 
    }
    scc.push_back(ve);
  }
}

缩点

缩点，就是把一个 SCC 缩成一个点，把他变成 DAG，这样想干啥就干啥就可以进行 dp 了！

把不同的 SCC 来建边，这样想干啥就干啥。

代码（Tarjan 代码省略）：

void solve() {
    for (int i = 1; i <= n; i++) {
        for (auto v : edges[i]) {
            if (bel[i] != bel[v]) {
                G[bel[i]].push_back(bel[v]);
            }
        }
    }
}

边双连通分量

无向图中，如果任意删去一边之后任意两点之间还可达，那么我们就称它是边双连通的。

边双连通其实把 \(Tarjan\) 的有向边换成无向边就可以了。

注意：重边！！！

代码：

inline void Tarjan(int u, int from) {
  dfn[u] = low[u] = ++idx; 
  stk[++top] = u;
  ins[u] = 1;
  int mark = 0;
  for (auto v : edges[u]) {
    if (v == from && !mark) {
      mark = 1;
    } else if (!dfn[v]) {
      Tarjan(v, u);
      low[u] = min(low[u], low[v]);
    }else if (ins[v]){
      low[u] = min(low[u], dfn[v]);
    }
  }
  if (low[u] == dfn[u]) {
    vector <int> ve;
    while (1) {
      int v = stk[top--];
      ins[v] = 0;
      ve.push_back(v);
      if (v == u) break; 
    }
    scc.push_back(ve);
  }
}

相同颜色的点为同一个连通分量！！！

后记

今天，我询问 Joler 老师：“什么时候要用点双，什么时候要用边双？”，Joler 老师笑而答曰：“请听下回分解（下节课再讲）”。