堆

堆

小根堆：特点根结点是最小值，并且每棵子树的根结点是这棵子树的最小值。

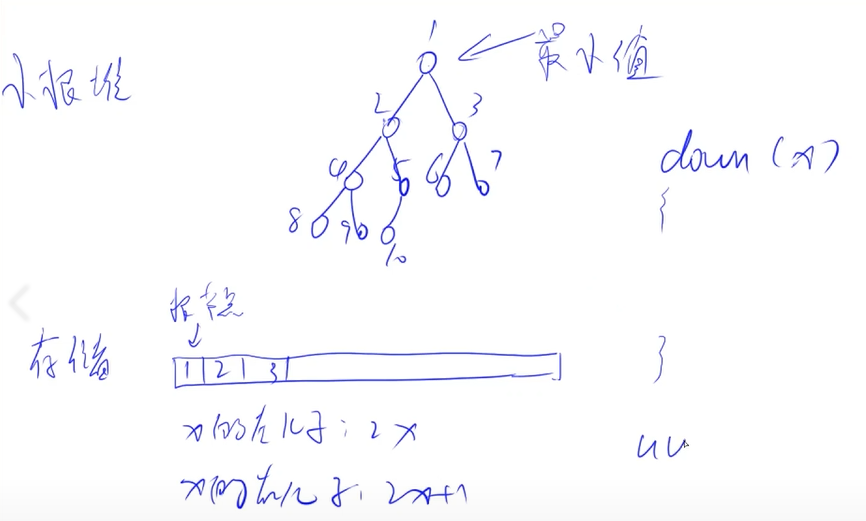
注意存储的时候下标从1开始。

堆排序

输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。

输入格式

第一行包含整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

输出格式

共一行，包含 m 个整数，表示整数数列中前 m 小的数。

数据范围

1≤m≤n≤10⁵
1≤数列中元素≤10⁹

输入样例：

5 3
4 5 1 3 2

输出样例：

1 2 3

代码：

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 100010;

int n, m;
int h[N], size;

void down(int u) {
    int t = u;

    if (u * 2 <= size && h[u * 2] < h[t]) {
        t = u * 2;
    }
    if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) {
        t = u * 2 + 1;
    }

    if (u != t) {
        swap(h[u], h[t]);
        down(t);
    }

}


void up(int u) {
    while (u / 2 && h[u / 2] > h[u]) {
        swap(h[u / 2], h[u]);
        u /= 2;
    }
}

int main() {

    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i++) {
        scanf("%d", &h[i]);
    }

    size = n;

    //以时间负责度为O(n)来创建堆
    for (int i = n / 2; i; i--) {
        down(i);
    }


    while (m--) {
        printf("%d", h[1]);
        h[1] = h[size];
        size--;
        down(1);
    }
    

}

模拟堆

维护一个集合，初始时集合为空，支持如下几种操作：

1. I x，插入一个数 x；
2. PM，输出当前集合中的最小值；
3. DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；
4. D k，删除第 k 个插入的数；
5. C k x，修改第 k 个插入的数，将其变为 x；

现在要进行 N 次操作，对于所有第 2 个操作，输出当前集合的最小值。

输入格式

第一行包含整数 N。

接下来 N 行，每行包含一个操作指令，操作指令为 I x，PM，DM，D k 或 C k x 中的一种。

输出格式

对于每个输出指令 PM，输出一个结果，表示当前集合中的最小值。

每个结果占一行。

数据范围

1≤N≤10⁵
−109≤x≤10⁹
数据保证合法。

输入样例：

8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM

输出样例：

-10
6

#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;

const int N = 100010;

//ph[k]表示第k个插入数的下标， hp[k]表示某个点是第几个插入的点
int ph[N], hp[N];
int h[N], size_s;

void heap_swap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}


void down(int u) {
    int t = u;

    if (u * 2 <= size_s && h[u * 2] < h[t]) {
        t = u * 2;
    }
    if (u * 2 + 1 <= size_s && h[u * 2 + 1] < h[t]) {
        t = u * 2 + 1;
    }

    if (u != t) {
        heap_swap(u, t);
        down(t);
    }

}


void up(int u) {
    while (u / 2 && h[u / 2] > h[u]) {
        heap_swap(u / 2, u);
        u /= 2;
    }
}

int main() {
    int n, m = 0;
    //scanf("%d%d", &n, &m);
    cin >> n;




    while (n--) {
        char op[10];
        int k, x;
        //scanf("%s", op);
        cin >> op;
        if (!strcmp(op, "I")) {
            cin >> x;
            //scanf("%d", &x);
            size_s++;
            m++;
            ph[m] = size_s;
            hp[size_s] = m;
            h[size_s] = x;
            up(size_s);
        }
        else if (!strcmp(op, "PM")) {
            printf("%d\n", h[1]);
        }
        else if (!strcmp(op, "DM")) {
            heap_swap(1, size_s);
            size_s--;
            down(1);
        }
        else if (!strcmp(op, "D")) {
            //scanf("%d", &k);
            cin >> k;
            k = ph[k];
            heap_swap(k, size_s);
            size_s--;
            down(k);
            up(k);
        }
        else {
            //scanf("%d%d", &k, &x);
            cin >> k >> x;
            k = ph[k];
            h[k] = x;
            down(k);
            up(k);
        }
    }
    return 0;

}