回溯专题其三（子集篇）

回溯专题其三（子集篇）

一，子集类问题解题思路

子集、组合、分割类问题的回溯框架非常相似，都能抽象为一棵树来遍历解空间。
不同点在于：

• 组合 / 分割问题：通常在树的 叶子节点 收集结果。
• 子集问题：则在树的 所有节点 收集结果，因为子集本身没有固定长度限制。

以 子集 78 为例，假设给定一个集合 mySet = ["a","b","c"],要求找出其所有子集
画出树形结构可以看到，树中的每一个节点对应着一个结果。

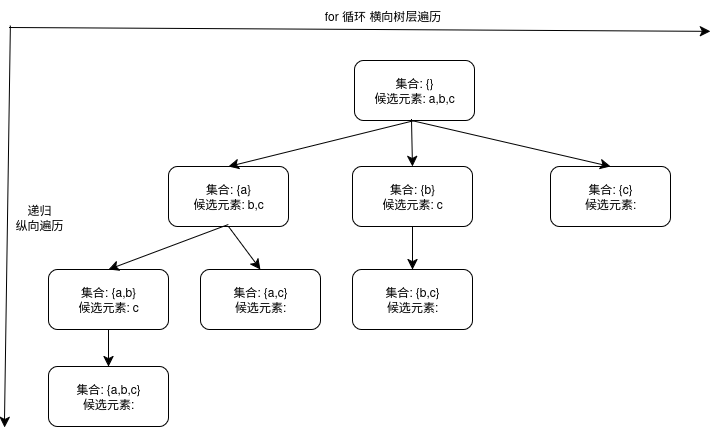
因此，解法核心就是：

• 使用 path 记录当前子集
• 在 每次递归进入节点时 把 path 加入结果集
• 继续递归扩展，直到遍历完数组

---

二，具体代码实现

Leetcode题单:

子集 78
子集II 90
递增子序列 491

1. 子集 78

思路:

• 在每个递归节点都把当前 path 加入结果集。
• 不需要额外的约束条件，直接遍历整棵子集树即可。

具体代码实现:

class Solution:
    def backtracking(self, nums: List[int], startIdx: int) -> None:
        if startIdx >= len(nums):
            return

        for i in range(startIdx, len(nums)):
            self.path.append(nums[i])
            self.result.append(self.path.copy())  # 在每个节点收集结果
            self.backtracking(nums, i+1)
            self.path.pop()

    def subsets(self, nums: List[int]) -> List[List[int]]:
        self.path = []
        self.result = [[]]  # 初始化包含空集
        self.backtracking(nums, 0)
        return self.result

2. 子集II 90

思路:

• 在 78 的基础上，需要 去重。
• 先对数组排序，保证相同元素相邻。
• 在递归时，利用 used 数组来避免同一层重复选择相同元素。

具体代码实现:

class Solution:
    def backtracking(self, nums: List[int], startIdx: int, used: List[bool]) -> None:
        if startIdx >= len(nums):
            return

        for i in range(startIdx, len(nums)):
            # 去重逻辑：同层相同元素只取一次
            if i > 0 and nums[i] == nums[i-1] and used[i-1] == False:
                continue

            self.path.append(nums[i])
            self.result.append(self.path.copy())
            used[i] = True
            self.backtracking(nums, i+1, used)
            used[i] = False
            self.path.pop()

    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        self.path = []
        self.result = [[]]
        nums.sort()
        used = [False] * len(nums)
        self.backtracking(nums, 0, used)
        return self.result

3. 递增子序列 491

思路:

• 本质上也是子集问题，但需要满足 子序列递增 的约束。

• 在每层递归中：

  • 若 path 长度 ≥ 2，则加入结果集。
  • 用一个 used 集合来避免同层重复选择相同数字。
  • 若当前元素小于 path 的最后一个元素，则跳过。

具体代码实现:

class Solution:
    def backtracking(self, nums: List[int], startIdx: int) -> None:
        if len(self.path) >= 2:
            self.result.append(self.path.copy())

        if startIdx >= len(nums):
            return

        used = []
        for i in range(startIdx, len(nums)):
            if nums[i] in used:  # 树层去重
                continue
            if self.path and nums[i] < self.path[-1]:  # 保持数组中元素递增
                continue
            self.path.append(nums[i])
            self.backtracking(nums, i+1)
            self.path.pop()
            used.append(nums[i])

    def findSubsequences(self, nums: List[int]) -> List[List[int]]:
        self.path = []
        self.result = []
        self.backtracking(nums, 0)
        return self.result

---

三，小结

子集类问题与组合、分割类问题最大的不同在于 收集结果的时机：

• 组合 / 分割：在 叶子节点 收集结果
• 子集：在 所有节点 收集结果

具体差异：

• 子集 78：基础回溯模板，无额外的约束条件
• 子集 II 90：在 78 的基础上增加 同层去重（排序 + used 数组）
• 递增子序列 491：在子集问题上增加 递增约束 + 同层去重