基于高斯过程回归的微波光子滤波性能提升的解调系统

📚 使用须知

• 本博客内容仅供学习参考
• 建议理解思路后独立实现
• 欢迎交流讨论

---

task : 基于高斯过程回归的微波光子滤波性能提升的解调系统

引言

该研究引入强大的机器学习工具高斯过程回归( Gaussian process regression，GPR )对微波光子滤波解调进行升级，提高了解调速度和精度。在基于光纤布拉格光栅(FBG)的微波光子滤波应变传感解调系统中，GPR被用来学习微波光子滤波器的频率响应与FBG上施加的应变之间的关系。

与传统的检测方法相比，所提方法在稀疏采样的频率响应下能够获得更好的测量精度，同时询问速度也得到了极大的提高。 更重要的是，训练好的GPR模型对于陷波深度波动较大的滤波器频率响应仍然有效，大大提高了对器件参数偏差和环境变化的容差。

系统结构与工作原理

其核心原理是构建一个双FBG的两抽头陷波MPF。

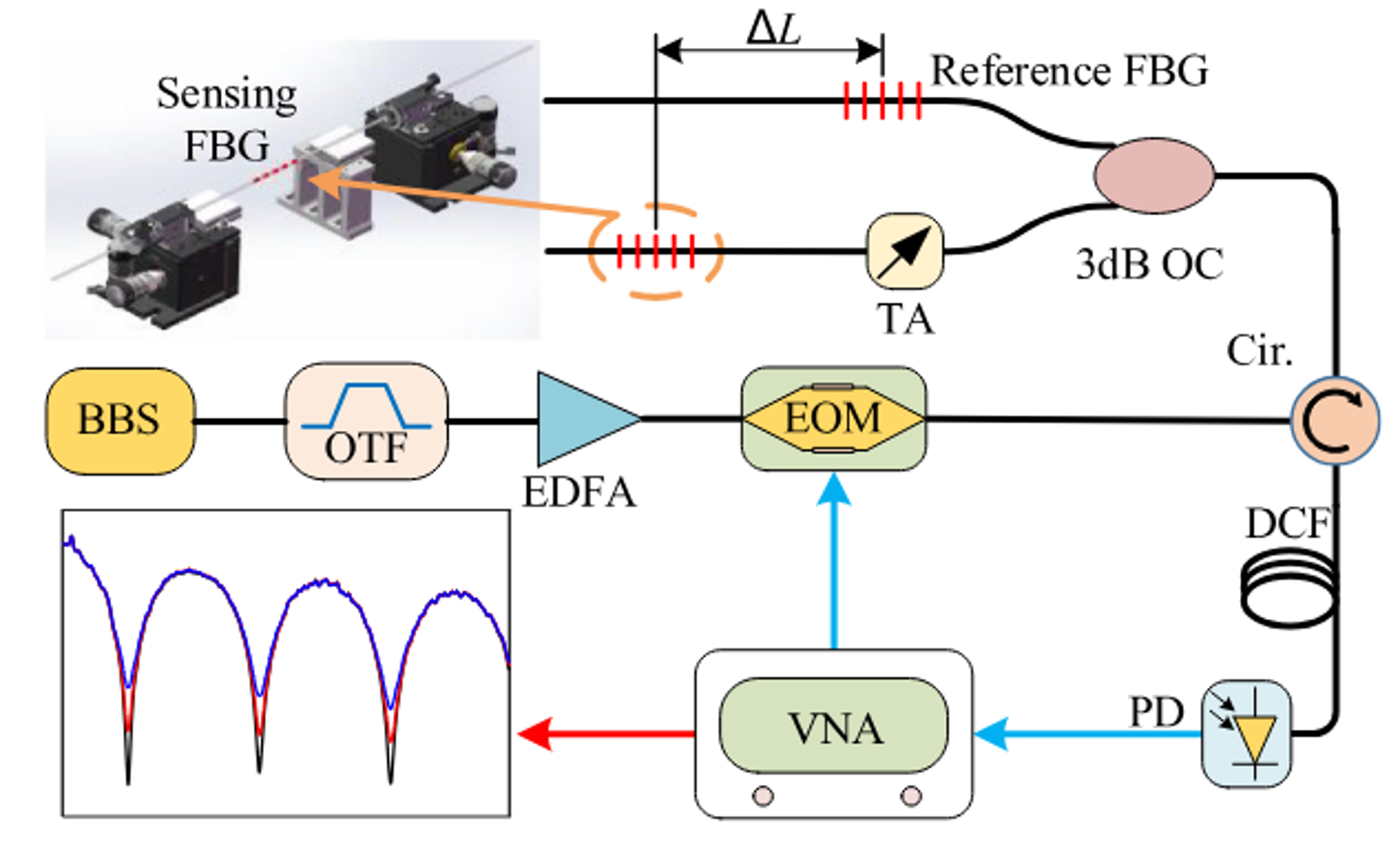
在VNA采集到频率响应数据后，引入了一个高斯过程回归（GPR）机器学习模型。

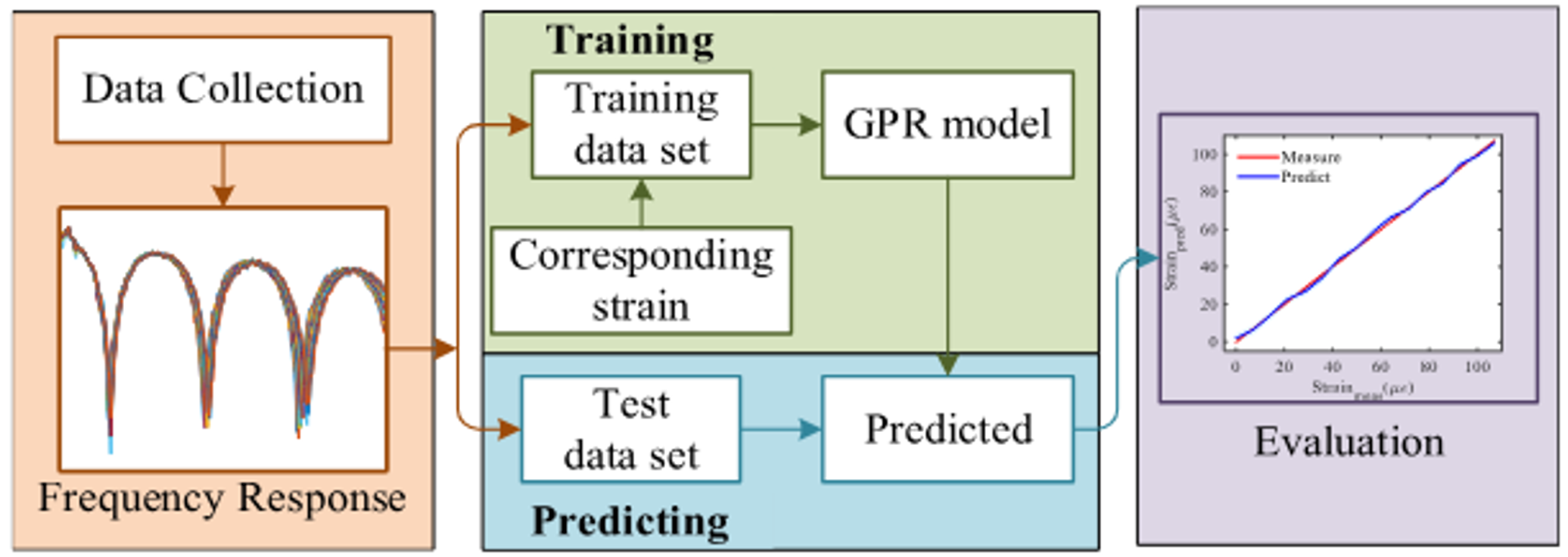
GPR是一种贝叶斯概率模型，它不对函数形式做具体假设，而是直接在函数空间上定义先验分布。

输入：不再是单个陷波频率，而是整条频率响应曲线；输出：对应的应变值。

实验验证与性能分析

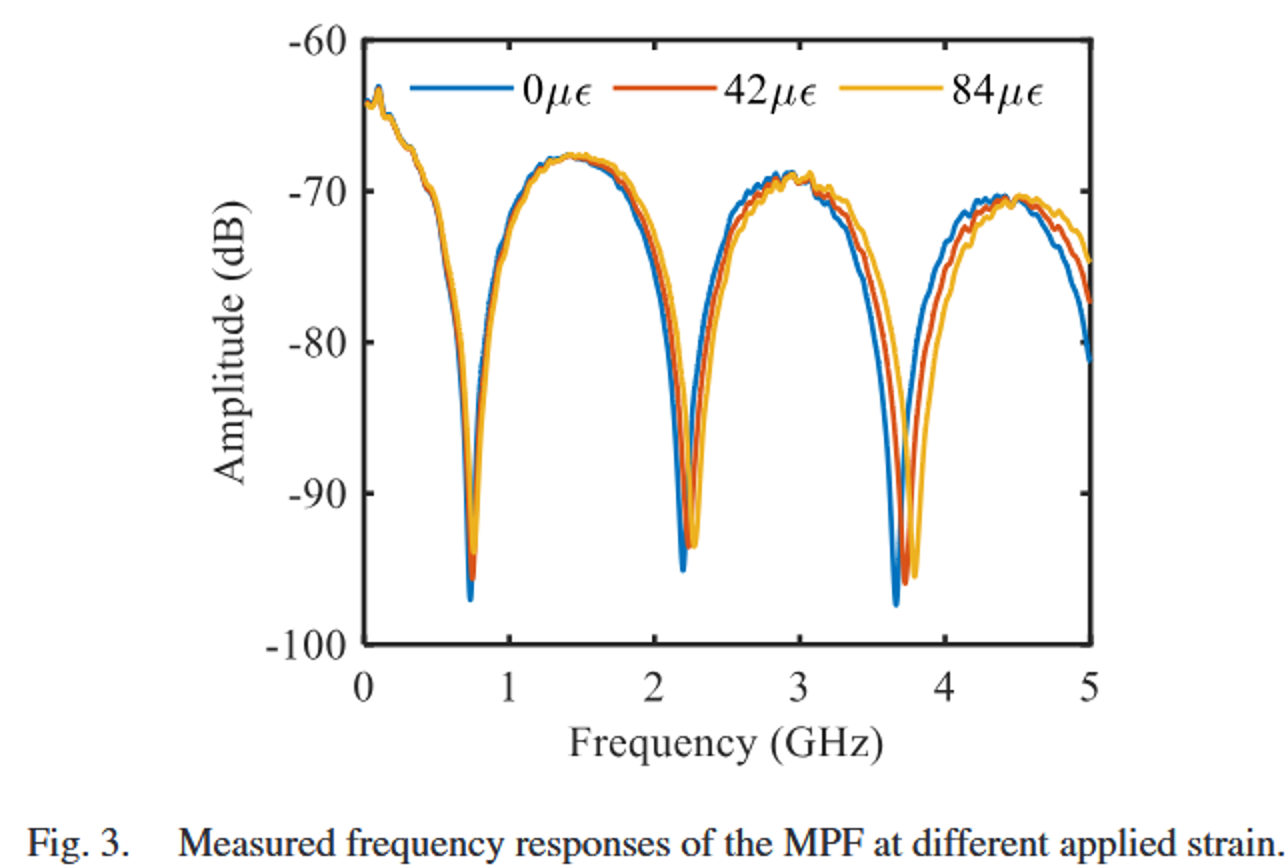
图3：展示了在不同应变（0-98 µε）下，MPF系统的频率响应（S21参数）曲线。

应变增加 → 波长差增大 → 时延差变化 → 陷波频率移动。

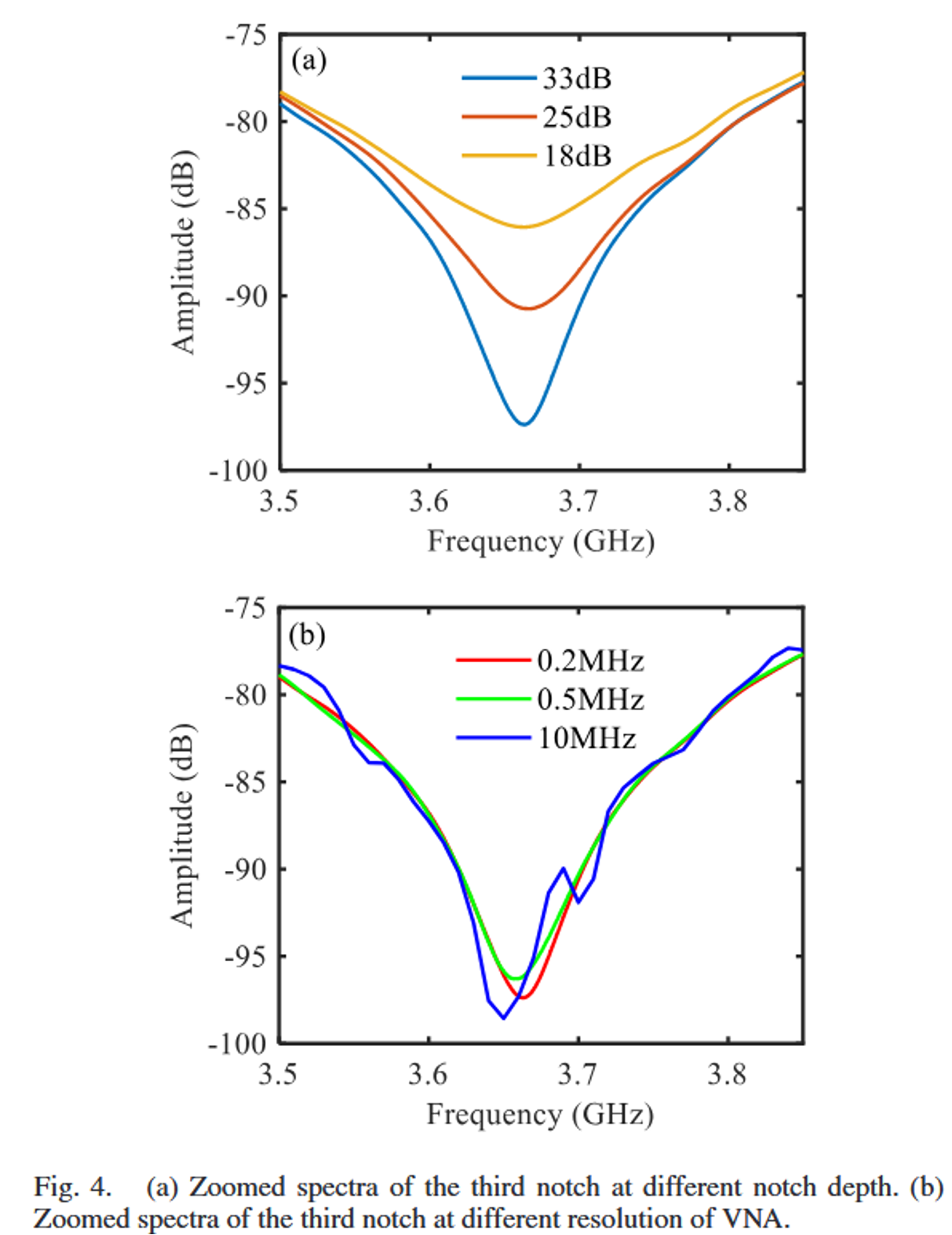
图4(a)：固定分辨率下，调整陷波深度（从18dB-33dB）。陷波越浅，其底部越平坦，频率定位越模糊。

图4(b)：固定陷波深度下，改变VNA采样分辨率（从1MHz-10MHz）。分辨率越低，采样点越稀疏，不仅陷波定位不准，连频谱形状都严重失真。

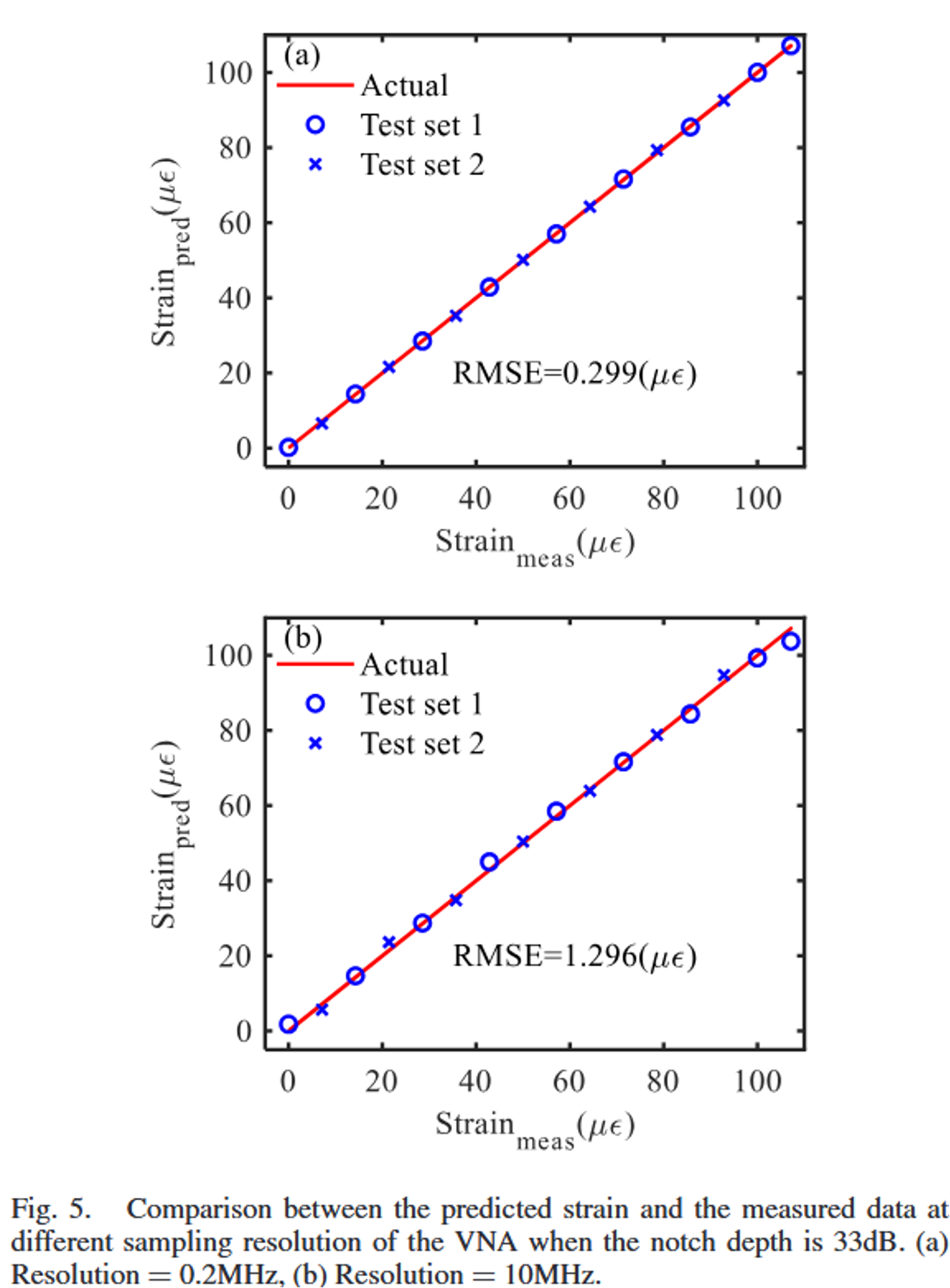
图5：对比在高分辨率(0.2MHz) 和低分辨率(10MHz) 下，GPR模型预测应变与实际应变的散点图。

图5(a)高分辨率：预测点紧密分布在参考线两侧，RMSE极低（0.299 µε），说明模型本身能力强大。

图5(b)低分辨率：尽管分辨率恶化了50倍，采样点变得非常稀疏，但GPR预测点依然高度贴合参考线，RMSE仅升至1.296 µε。相比之下，文中提到传统方法在此分辨率下误差已超4.8 µε。

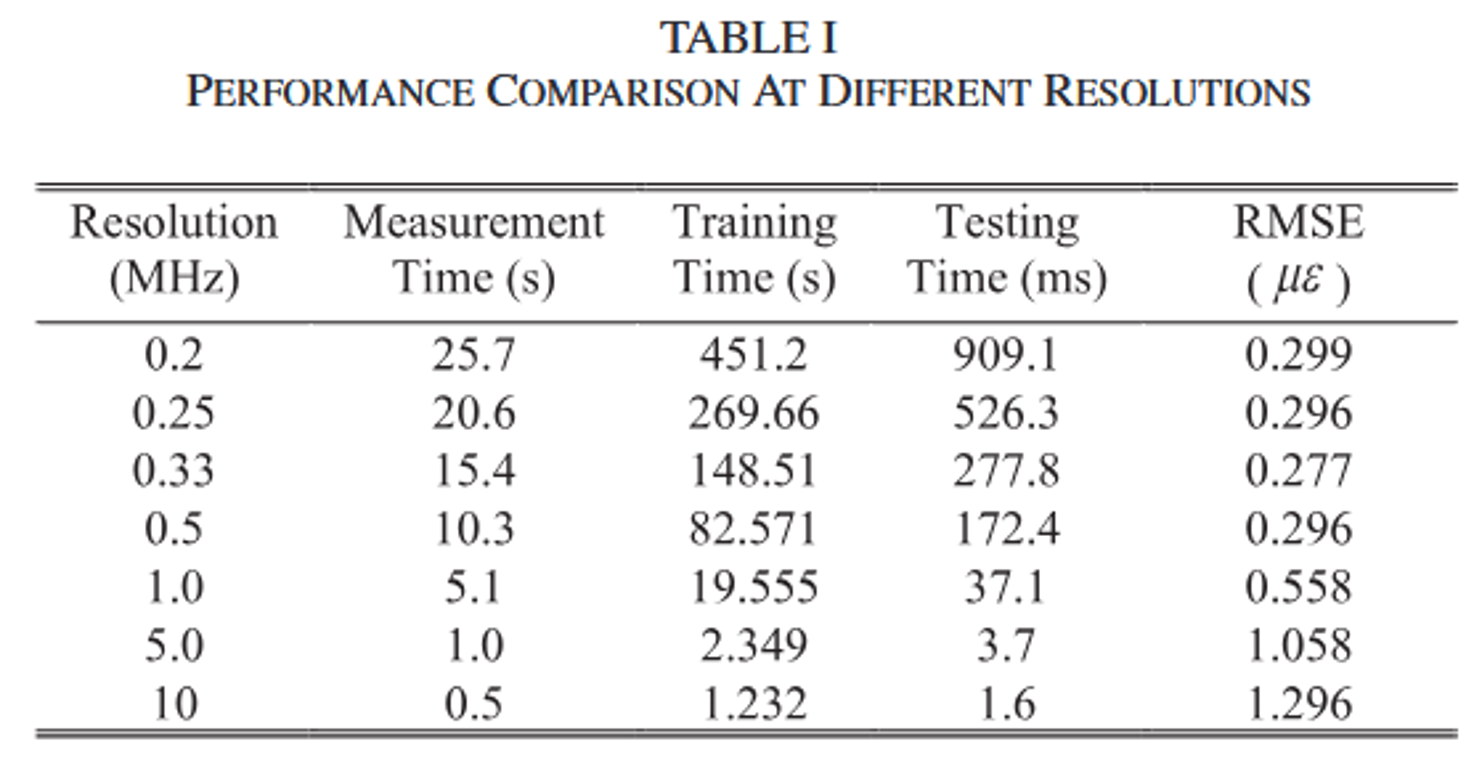
表一系统地评估了在不同矢量网络分析仪（VNA）采样分辨率下，GPR辅助系统的完整性能指标。

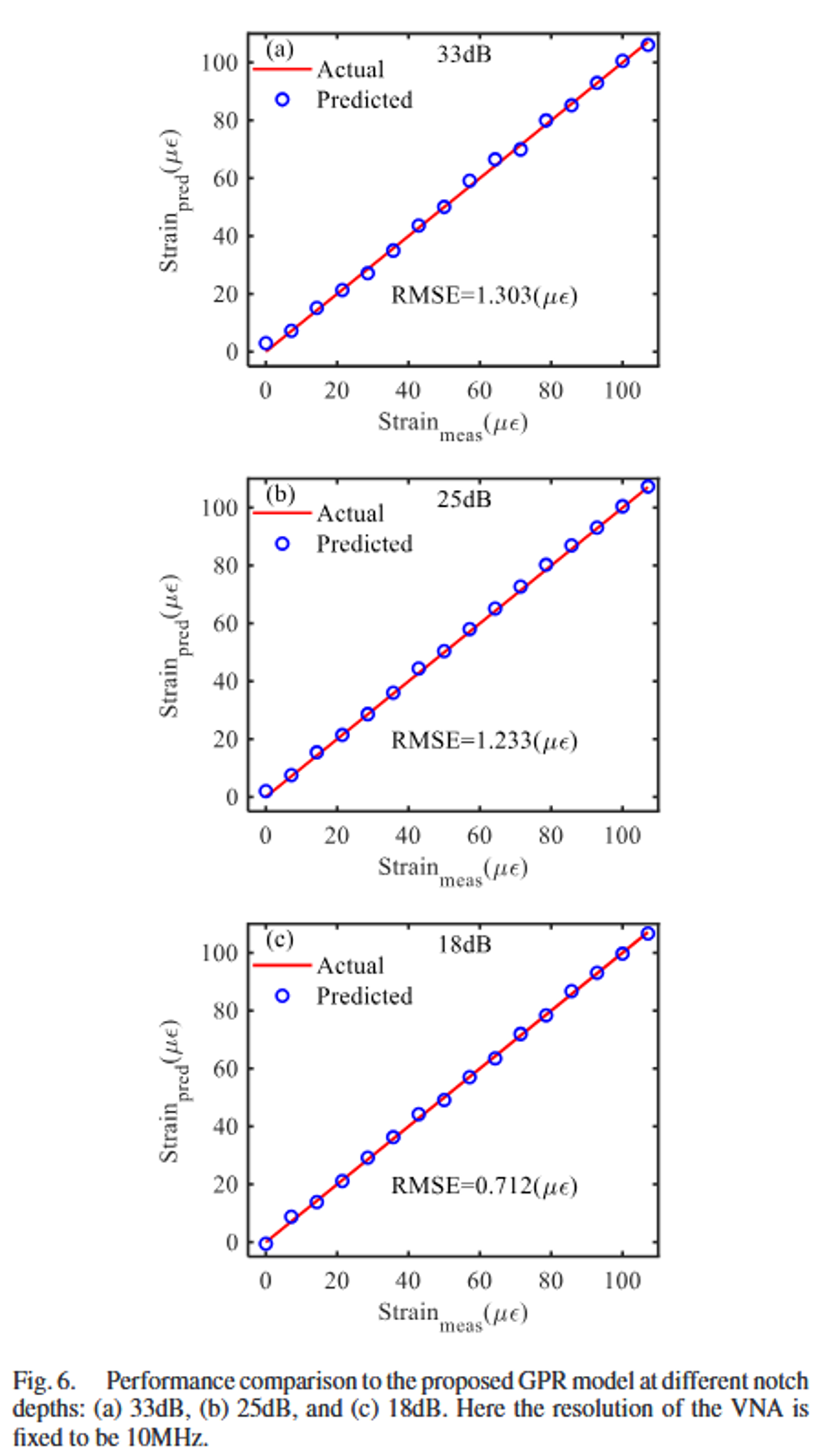
图6：展示了在33dB, 25dB, 18dB三种不同陷波深度下，GPR模型预测应变的散点图。模型仅用18dB和33dB的数据训练。

在训练过的33dB和18dB深度下，预测精准（RMSE分别为1.303和0.712 µε）。最关键的是在未训练过的25dB深度下，预测同样精准（RMSE为1.233 µε）。

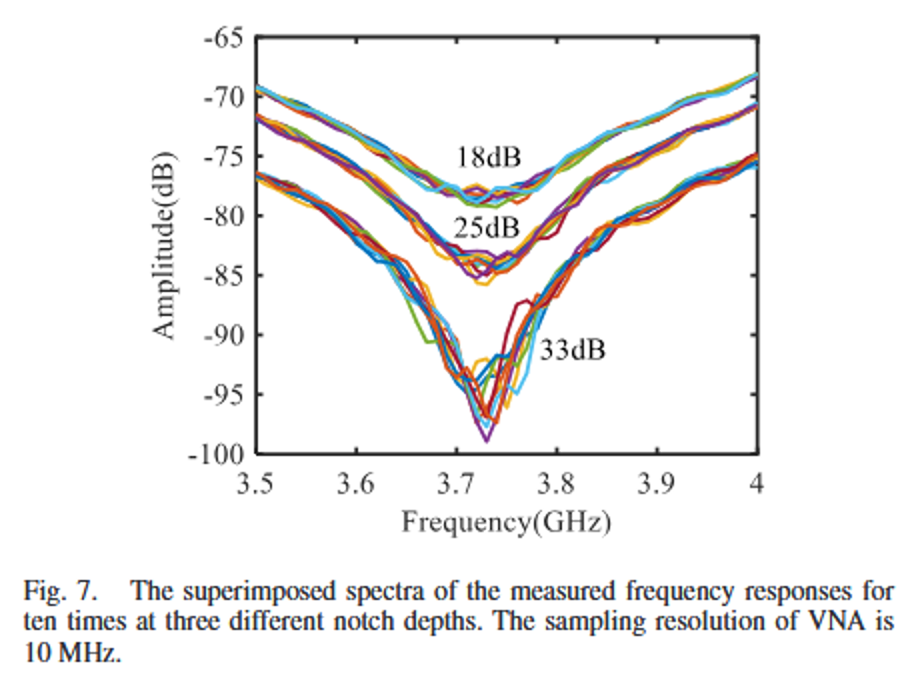
图7：将同一条件下（固定应变）连续10次扫描得到的频谱片段（聚焦于一个陷波）叠加显示。陷波的深度和形状在每次扫描中都会自然波动。