基于相控微波光子滤波器的旋转诱导相位差解调
级联MRR-ODSB-MPF
📚 使用须知
- 本博客内容仅供学习参考
- 欢迎交流讨论
研究背景
基于Sagnac效应的光纤陀螺仪在惯性导航中具有重要应用,传统解调方法包括:
干涉强度法:结构简单但非线性严重,动态范围有限;
相位法:线性度好,但易受光学非互易性影响;
谐振腔法:灵敏度高,但受背向散射噪声影响大;
光电振荡器法:具有高比例因子,但频率稳定性与自由谱范围限制精度。
研究目标
提出一种基于相位控制微波光子滤波器 的灵活解调方案,用于高灵敏度、高灵活性地测量旋转引起的Sagnac相位差,并实现:
频率响应偏移监测;
特定频率下功率变化测量;
灵敏度可调、结构简单的旋转速率检测系统。
研究创新点
首次将相位控制MPF应用于Sagnac相位解调,将旋转引起的相位差映射为MPF频率响应的偏移;
提出两种解调方式:
使用VNA监测MPF频率响应;
使用功率计监测特定调制频率下的功率变化;
灵敏度可调:通过调节偏振控制器或选择不同工作频率实现;
系统结构相对简单,兼具高灵敏度与灵活性。
研究方法
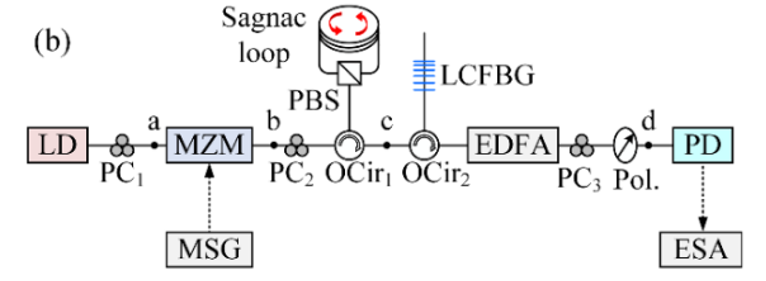
系统结构:
激光器 → ODSB调制器 → Sagnac环(PMF)→ LCFBG → 偏振器 → 光电探测器;
使用偏振分束器分离载波与一阶边带,使其在Sagnac环中反向传播;
理论建模:建立了MPF频率响应与旋转相位差之间的数学关系;
实验验证:
使用VNA测量MPF频率响应随旋转速率的变化;
使用微波信号源与频谱分析仪测量功率变化;
参数调节:通过PC₃调节相位偏置,优化系统工作点。
核心原理
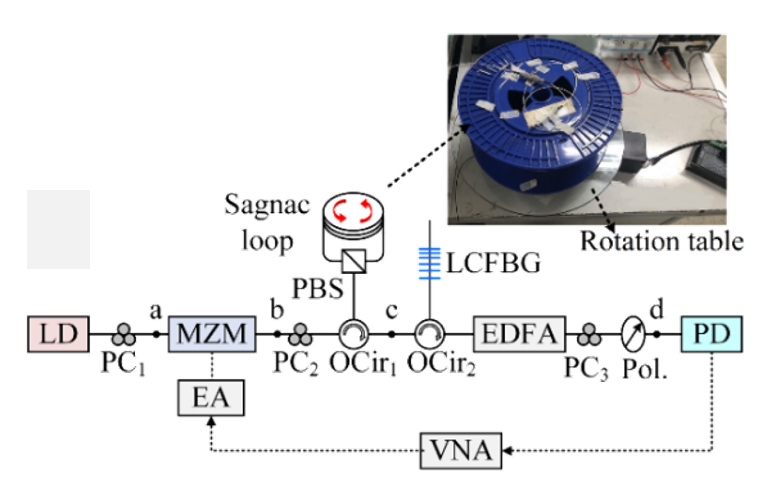
首次将相位控制MPF用于Sagnac解调。将旋转引起的相位差 Δφ,通过色散元件,转化为微波光子滤波器的频率响应偏移。两种解调模式:模式一,监测MPF频率响应的偏移;模式二,监测固定微波频率下的功率变化。
ODSB调制:MZM产生偏振正交的载波和一阶边带。
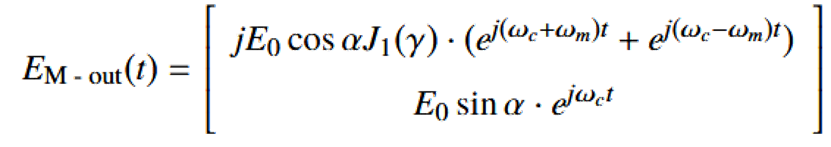
偏振分离与Sagnac环:偏振分束器将载波和边带分开,使其在Sagnac环中反向传播,引入旋转相位差 Δφ。
LCFBG引入色散:线性啁啾光纤光栅对不同频率成分引入不同的相位延迟 θi。
光信号经偏振器干涉,被光电探测器拍频,最终形成MPF的频率响应。
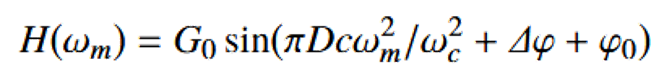
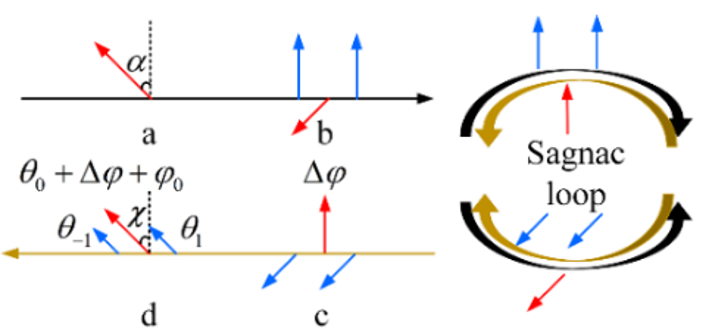
系统频谱演化示意图
图题:Schematic spectrum evolution at different locations.
中文释义: 在不同位置(节点)的信号频谱示意图。
这张图描绘了光信号从产生、调制、分离、相移到最终合成并转化为电信号的整个过程中,其频谱结构发生的变化。我们可以沿着系统的光路,分步骤解析:
激光器输出 & ODSB调制后
第一个图(最左边): 从激光器发出的原始光载波。它就是一个单一的、高纯度的光谱线,频率为 ω_c。
第二个图(经过MZM后): 这是整个过程的第一个关键创造。
经过工作在最小传输点的正交双边带调制器后,输入的单一路偏振光被调制。
产生了什么? 一个正交双边带信号。
中心是光载波,其偏振方向我们记为 Y方向(如图中竖线所示)。
两侧是一阶边带,它们的频率分别是 ω_c + ω_m 和 ω_c - ω_m,而它们的偏振方向与载波正交,记为 X方向(如图中圆点所示)。
核心特征: 载波和边带在频率上分开,在偏振上正交。这为后续在Sagnac环中将它们分离并使其反向传播奠定了基础。
Sagnac环与偏振分束器
第三个图(PBS后): 这是第二个关键操作。
偏振分束器根据偏振态将输入光信号分到两个不同的端口。
上路(CW,顺时针): 假设它只包含了Y偏振的光载波。
下路(CCW,逆时针): 假设它只包含了X偏振的两个一阶边带。
注意: 理想情况下是完全分离,但实际中可能存在残余,如论文后面讨论的误差源所述。
引入旋转效应与LCFBG反射
第四个图(LCFBG反射后): 这一步包含了两个重要的物理效应。
Sagnac效应: 由于整个环路在旋转,以相反方向传播的载波和边带之间会积累一个旋转诱导的相位差 Δφ。这个相位差本身在光谱上看不出来,但它已经烙印在光的相位信息中。
LCFBG的色散效应: LCFBG对不同频率的光反射位置不同,因此给载波 (ω_c)、上边带 (ω_c + ω_m) 和下边带 (ω_c - ω_m) 引入了不同的相位延迟 θ_0, θ_1, θ_-1(如公式(4)所示)。
所以,反射后的信号可以理解为:频率成分没有变,但每个频率成分的相位都发生了改变,并且载波与边带之间还多了一个相对相位 Δφ。
偏振器合成与拍频
第五个图(经过偏振器后): 这是第三个关键操作。
偏振器的作用相当于一个“偏振合束器”,它只允许一个特定方向的光通过。因此,原本偏振正交的载波和两个边带,现在被投影到同一个偏振方向上。
发生了什么? 它们之间可以发生干涉了。现在在光电探测器的输入端,我们有三个频率成分在同一偏振态上:一个载波和两个边带。
光电探测与MPF形成
第六个图(光电探测器后): 这是最终的转换。
光电探测器是平方律器件,它响应光的强度。当载波和边带在探测器上相干拍频时,会产生新的频率成分。
具体过程:
载波 (ω_c) 和上边带 (ω_c + ω_m) 拍频,产生 ω_m 的微波信号。
载波 (ω_c) 和下边带 (ω_c - ω_m) 拍频,也产生 ω_m 的微波信号。
这两个来自双边带的微波信号之间的相对相位,正好包含了之前引入的所有相位信息:θ_1 - θ_0 - Δφ 和 θ_0 - θ_-1 + Δφ 等。经过推导(如公式(6)和(7)),最终合成的微波信号的幅度与 sin( ... + Δφ + φ_0) 成正比。
最终结果: 输出的电频谱在微波频率 ω_m 处有一个单峰,而这个峰的幅度(对应功率) 就是整个微波光子滤波器的频率响应 H(ω_m)。当 Δφ 随旋转改变时,这个幅度响应曲线就会在整个频带上发生平移,如Figure 2(a)和Figure 5(a)所示。
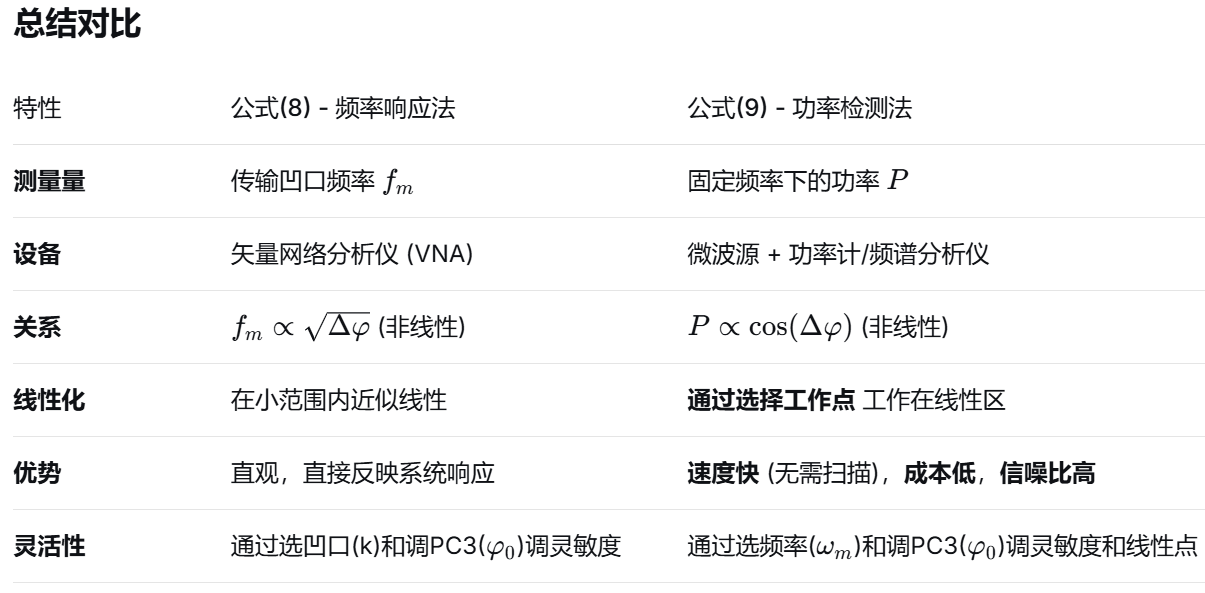
两种解调模式:模式一,监测MPF频率响应的偏移。
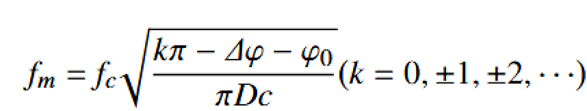
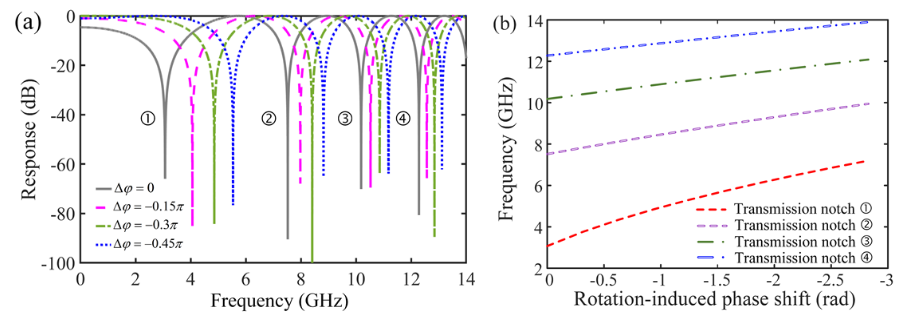
图(a):不同旋转引起的相位差下的仿真频率响应;
图(b):不同传输槽处的频率与相位差的函数。
频移随着传输陷波数的增加而减小,这意味着在较低的陷波频率下获得了较高的测量灵敏度。
模式二,监测固定微波频率下的功率变化。在一定的调制频率下,通过监测PD输出的信号强度可以解调出转速:
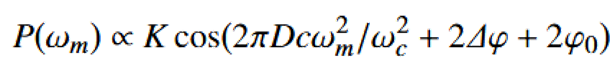
在固定微波频率ωm下,输出功率P是Δφ的函数。




实验结果
随着转速增加,MPF的频率响应确实发生了漂移;在1 rad/s时,第一、二、三陷波的偏移量分别为1.7 GHz, 1.1 GHz, 0.7 GHz;第一陷波灵敏度最高,最低可测转速达 1.3 °/h。功率与转速有良好的线性关系;在4 GHz下,可达 0.013 °/h。
基于MPF频率响应偏移的解调
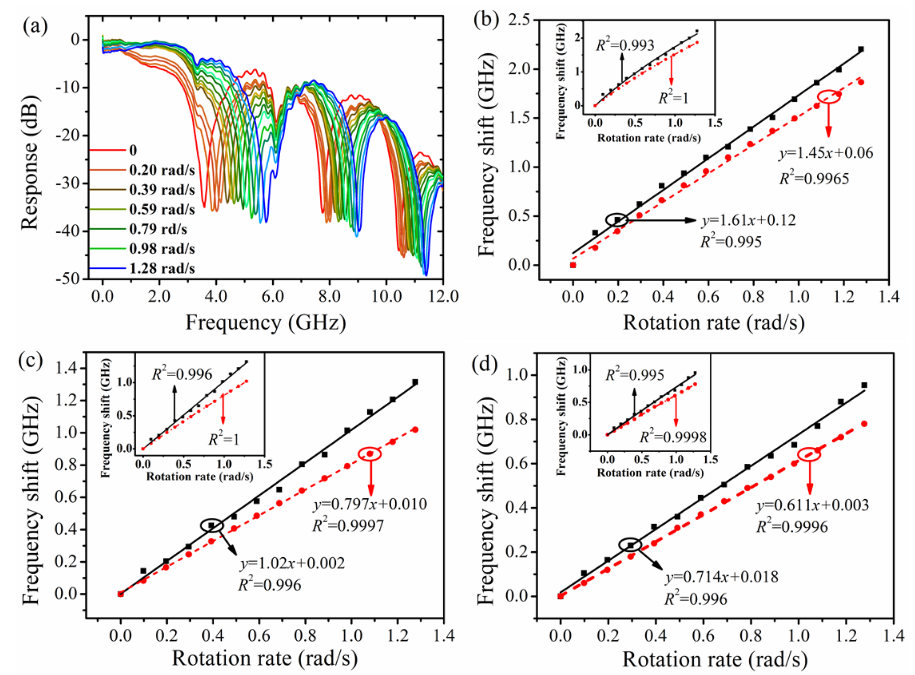
图题: (a) 不同转速下测得的MPF频率响应。(b)(c)(d) 分别为第一、二、三传输凹口的频率偏移与转速的关系。
(a):频率响应的直观变化
内容: 这是一组在矢量网络分析仪上测得的S21曲线,展示了MPF的频率响应如何随旋转速率(0 到 1.276 rad/s)变化。
关键观察:
整体漂移: 随着转速增加,整个频率响应曲线(包括所有的通带和阻带)向高频方向移动。这直观地证明了公式(8)的正确性——Δφ的增加导致了凹口频率f_m的增加。
凹口清晰度: 传输凹口(即“谷”)非常尖锐,这使得我们能够精确地定位其中心频率。
验证理论: 这个现象与Figure 2(a)的理论模拟完全对应,证实了“旋转导致相位差,相位差导致MPF频率响应偏移”的核心原理。
(b), (c), (d):定量分析与性能评估
这三个子图分别对第一、二、三个传输凹口进行了定量分析。
横轴: 旋转速率 (rad/s) 纵轴: 传输凹口的频率偏移 (GHz)
数据点:
黑点: 实验测量数据。红线: 根据公式(8)和系统参数进行的理论模拟数据。
拟合曲线:
插图内的拟合: 提供了线性拟合和非线性拟合 y = A(√(x+B) - √B) 的对比。
核心发现: 在实验测量范围内(0-1.276 rad/s),频率偏移与转速呈现出良好的近似线性关系。这使得数据处理变得简单。
三个子图的对比揭示了关键结论:
灵敏度差异:
第一凹口 (b): 在1 rad/s时,频率偏移高达 1.7 GHz。
第二凹口 (c): 偏移为 1.1 GHz。
第三凹口 (d): 偏移为 0.7 GHz。
结论: 凹口序号k越小(频率越低),对转速的灵敏度越高。这与公式(8)中f_m与k的关系一致。
测量精度:
文中指出,当VNA分辨率设为10 kHz时,三个凹口对应的最小可测转速分别为 1.3 °/h, 2.0 °/h, 和 3.4 °/h。
结论: 灵敏度越高,系统能探测到的微小转速变化就越小,即精度越高。
灵活性与设计空间:
启示: 在实际应用中,如果我们追求高精度测量微小转速,应选择第一凹口。如果我们需要一个更大动态范围且对精度要求稍低的系统,则可以选择更高序号的凹口。这体现了该方案的灵活性。
基于单频功率变化的解调
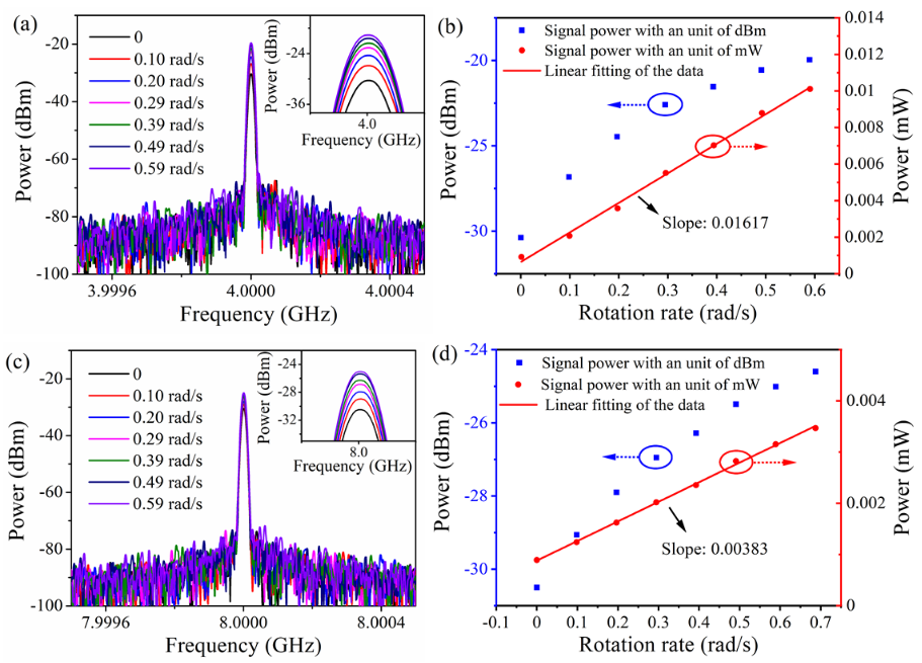
图题: (a) 在4 GHz调制频率下,不同转速时的电频谱。(b) 4 GHz处峰值功率与转速的关系。(c)(d) 在8 GHz下的相应结果。
(a) & (c):电频谱演变
内容: 这些图显示了在固定调制频率(4 GHz或8 GHz)下,光电探测器输出的微波信号频谱。
关键观察:
峰值功率变化: 随着转速的改变,频谱线的高度(即峰值功率) 发生了明显变化,而其频率位置保持不变。
信噪比: 信号峰非常突出,背景噪声很低,这表明该方法具有很高的信噪比,有利于精确测量功率。
(b) & (d):功率-转速关系与灵敏度
这是功率检测法的核心定量结果。
左纵轴(蓝线/点): 峰值功率,单位为 dBm(对数坐标)。
右纵轴(红线/点): 将dBm转换为mW(线性坐标)后的峰值功率。
横轴: 旋转速率 (rad/s)
核心分析:
工作点选择:
作者特意将调制频率设置在MPF通带的下降沿(如Figure 1(c)所示)。在这个区域,频率响应曲线的斜率很大,意味着频率的微小偏移会转化为强烈的功率变化。
从(b)的蓝线(dBm值)可以看到,在低转速区,功率随转速快速变化(线性区);当转速增大到一定程度,功率变化趋于平缓(饱和区)。这表明我们正工作在余弦函数公式(9)的线性区间到非线性区间的过渡带上。
比例因子与灵敏度:
在4 GHz时 (b): 当我们将功率单位转换为mW(红点)后,在有效的线性区间内,其斜率(即比例因子)为 0.016 mW/(rad/s)。
在8 GHz时 (d): 比例因子下降为 0.004 mW/(rad/s)。
结论: 4 GHz处的灵敏度是8 GHz处的4倍。这同样体现了灵活性——通过选择不同的调制频率ω_m,可以调整系统的灵敏度。
动态范围与最小可测转速:
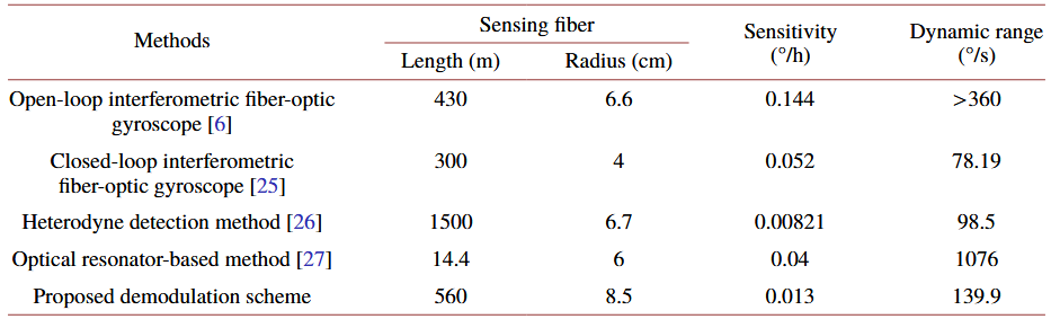
文中指出,在4 GHz下,考虑到系统噪声基底(-90 dBm),可计算得出最小可测转速高达 0.013 °/h。这个性能优于频率响应法,也优于Table 1中的许多传统方法。
原因: 功率检测法避免了VNA扫描,直接测量单频功率,通常具有更低的系统噪声。
研究结论
频率响应法:
在1 rad/s转速下,第一、二、三个传输凹口的频率偏移分别为1.7 GHz、1.1 GHz、0.7 GHz;
最低可测转速达 6.2×10−6 rad/s(约1.3°/h);
功率检测法:
在4 GHz调制频率下,比例因子为0.016 mW/(rad/s);
在8 GHz下为0.004 mW/(rad/s);
系统灵活性高,灵敏度与动态范围可根据需求调节;
与现有技术相比,性能相当但结构更简单、更灵活。
研究局限性
最大可测转速受限于MPF频率响应的周期(π相位差),实验中最大为2.44 rad/s;
系统稳定性受以下因素影响:
MZM偏置漂移;
偏振态波动;
温度引起的Shupe效应;
残余光载波与边带可能导致相位误差,需精确控制偏振与调制状态;
实验中使用的LCFBG色散值固定,限制了系统在某些应用中的灵活性。

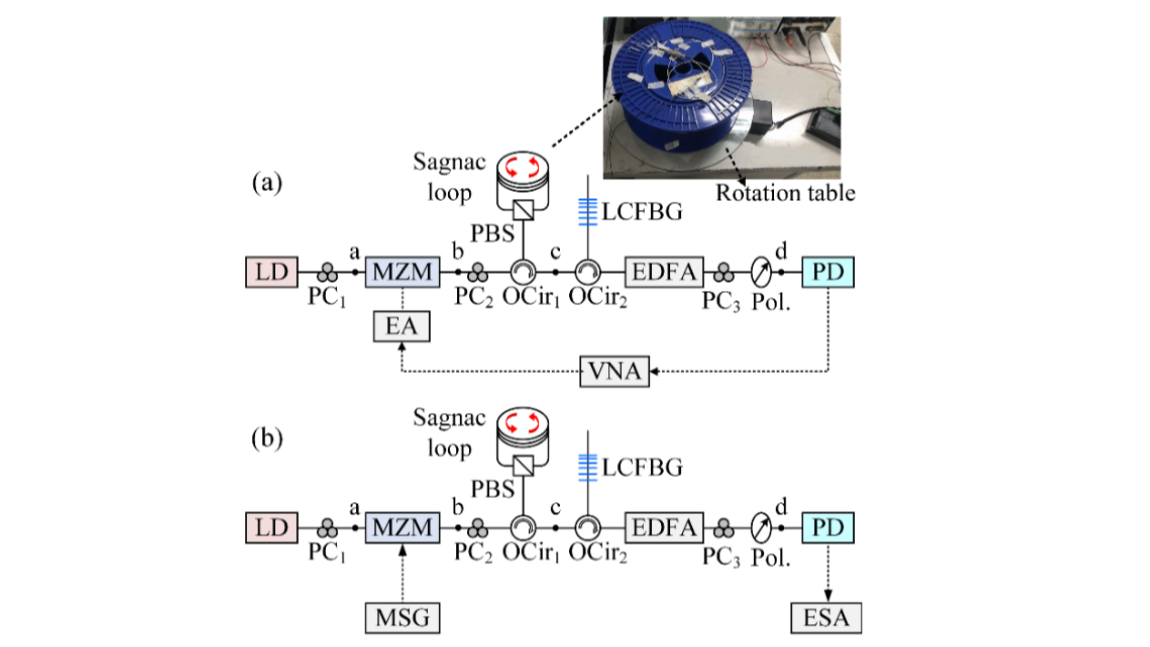 该研究提出了一种基于相位控制的微波光子滤波器(MPF)的旋转速率的测量。由于LCFBG的色散作用,MPF中心频率可以通过改变OC和一阶边带之间的相位差来调节。 因此,如果OC和一阶边带被偏振分束器分离,然后沿着Sagnac环反向传播,它们之间的旋转诱导相位差将导致MPF的频率响应发生偏移。
该研究提出了一种基于相位控制的微波光子滤波器(MPF)的旋转速率的测量。由于LCFBG的色散作用,MPF中心频率可以通过改变OC和一阶边带之间的相位差来调节。 因此,如果OC和一阶边带被偏振分束器分离,然后沿着Sagnac环反向传播,它们之间的旋转诱导相位差将导致MPF的频率响应发生偏移。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号