学习笔记-霍夫变换
霍夫变换
一、Hough变换的算法思想
二、直线检测
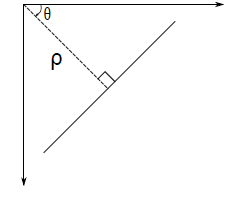
- 初始化一个二维累加器并设为0,累加器长度为max{θ的取值范围,ρ的取值范围},ρ最大取对角线的像素数。
- 选取(x,y)代入直线方程,对θ以步长s(比如1)从0到180遍历并求出ρ值,将累加器相应位置( ρ,θ) +1。
- 重复2过程,直到遍历完所有的点。
- 以阈值T筛选二位累加器内符合条件的参数对( ρ,θ),画图显示之。
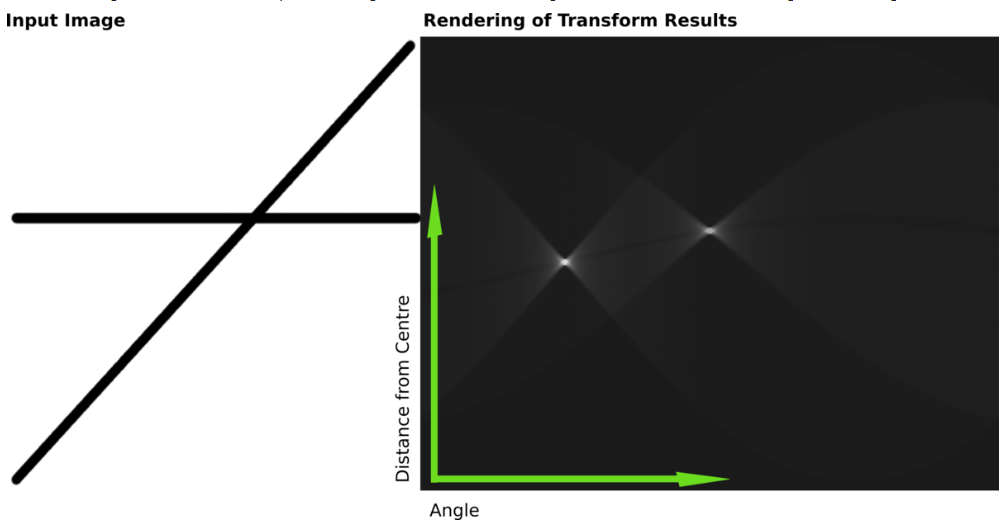
如果画出来参数空间图,应该是下图这样,右图的两个亮点就代表了左图的两条直线的参数( ρ,θ)。(from:https://en.wikipedia.org/wiki/Hough_transform)
另一个可供观看的动图例子:http://homepages.inf.ed.ac.uk/amos/hough.html
代码实现:

import cv2 import numpy as np import matplotlib.pyplot as plt # 1.准备工作 # 生成一张两直线的图片 img=np.zeros((512,512,1), np.uint8) cv2.line(img,(0,0),(511,511),255,20) cv2.line(img,(0,511),(511,0),255,20) # 显示 cv2.imshow('image',img) cv2.waitKey(0) # 保存 cv2.imwrite("images/2_lines.jpg",img) # 2.寻找边缘 img=cv2.imread("images/2_lines.jpg") #img=cv2.imread("images/1.jpg") img_edge = cv2.Canny(img, 50, 150) # 边缘显示 # cv2.imshow('image',img_edge) # cv2.waitKey(0) # 3.霍夫变换 lines = cv2.HoughLines(img_edge,10,np.pi/180,500) for i in range(len(lines)): rho=lines[i][0][0] theta=lines[i][0][1] a = np.cos(theta) b = np.sin(theta) x0 = a*rho y0 = b*rho x1 = int(x0 + 1000*(-b)) y1 = int(y0 + 1000*(a)) x2 = int(x0 - 1000*(-b)) y2 = int(y0 - 1000*(a)) cv2.line(img,(x1,y1),(x2,y2),(0,0,255),2) cv2.imshow('image',img) cv2.waitKey(0)
三、圆检测
image: 输入图像。
method: 固定填cv2.HOUGH_GRADIENT。这是霍夫圆检测的一种数学方法:梯度法,目前只有这一种已经实现。
dp: 计数器的分辨率图像像素分辨率与参数空间分辨率的比值(官方文档上写的是图像分辨率与累加器分辨率的比值,它把参数空间认为是一个累加器,毕竟里面存储的都是经过的像素点的数量),dp=1,则参数空间与图像像素空间(分辨率)一样大,dp=2,参数空间的分辨率只有像素空间的一半大,这个参数决定了参数的与分辨率相比的精度,一般设置为1,就是参数能精确到一个像素。类似于霍夫直线检测中θ的步长s。
minDist: 圆心之间最小距离,如果距离太小,会产生很多相交的圆,如果距离太大,则会漏掉正确的圆,防止检测出太多的圆。这一步需要先验知识:你已经知道图像中的圆最小相距多远。
默认参数:
param1: canny检测的双阈值中的高阈值,低阈值是它的一半,这涉及canny算法。
param2: 最小投票数(基于圆心的投票数),就类似于霍夫直线检测中的阈值T,它决定了某组参数是不是有圆,这个参数也得慢慢试,或者需要一些先验知识。
minRadius: 需要检测圆的最小半径,需要先验知识。
maxRadius:需要检测圆的最大半径,需要先验知识。

代码实现:

1 import cv2
2 import numpy as np
3 import matplotlib.pyplot as plt
4
5 # 1.寻找边缘
6 img=cv2.imread("images/3_circles.png")
7 img_edge = cv2.Canny(img, 50, 150)
8 # # 边缘显示
9 # cv2.imshow('image',img_edge)
10 # cv2.waitKey(0)
11 # 2.霍夫变换
12 circles = cv2.HoughCircles(img_edge,cv2.HOUGH_GRADIENT,1,100,param1=50,param2=30,minRadius=10,maxRadius=200)
13 # 3.画出检测到的圆
14 for i in circles[0,:]:
15 cv2.circle(img,(i[0],i[1]),i[2],(0,0,255),2) # 圆
16 cv2.circle(img,(i[0],i[1]),2,(0,0,255),3) # 圆心
17
18 cv2.imshow('image',img)
19 cv2.waitKey(0)
最后,还是要说说这个算法的优缺点。算法在数学上很漂亮,但计算量随参数个数指数级上升,直线检测需要两个参数,圆检测需要3个,椭圆检测需要5个,一般椭圆检测就需要一些快速搜索参数的算法,前面cv2.HoughCircles()的默认参数部分就是用来减小参数搜索范围的,另一个缺点就是受噪声影响大,太多的噪声会让霍夫变换彻底失去作用,这也是这类从数学原理出发的算法的老毛病:”过度精确“从而缺乏鲁棒性。所以如果输入图像质量还可以,用来检测圆形或者直线边缘还是挺好用的。
参考资料:
http://www.cnblogs.com/AndyJee/p/3805594.html
https://blog.csdn.net/yuyuntan/article/details/80141392




 浙公网安备 33010602011771号
浙公网安备 33010602011771号