【d2l】3.4.softmax回归

【d2l】3.4.softmax回归

此前的线性回归解决了“多少”的问题，而现实中的问题不止这种问题

还有一种占比很大的问题：分类问题。一般来讲，在机器学习中，我们使用“软性”分类，即用概率来代表属于某种事物的可能性

分类问题

首先的问题是如何用数学的语言表示分类的结果

独热编码（one-hot encoding）就是一种简单的方法，利用向量来表示，类别对应的分量设置为1，其他所有的都设置为0

比如我有分成三类的问题，可以如下表示：

\[y \in \{ (1, 0, 0), (0, 1, 0), (0, 0, 1) \} \]

网络架构

对于分类问题，假设有一个四个特征、三个类别的问题，可以构建出一个一层的神经网络，表示图与计算过程如下：

\[o_1 = x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1 \\ o_2 = x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_1 \\ o_3 = x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_1 \]

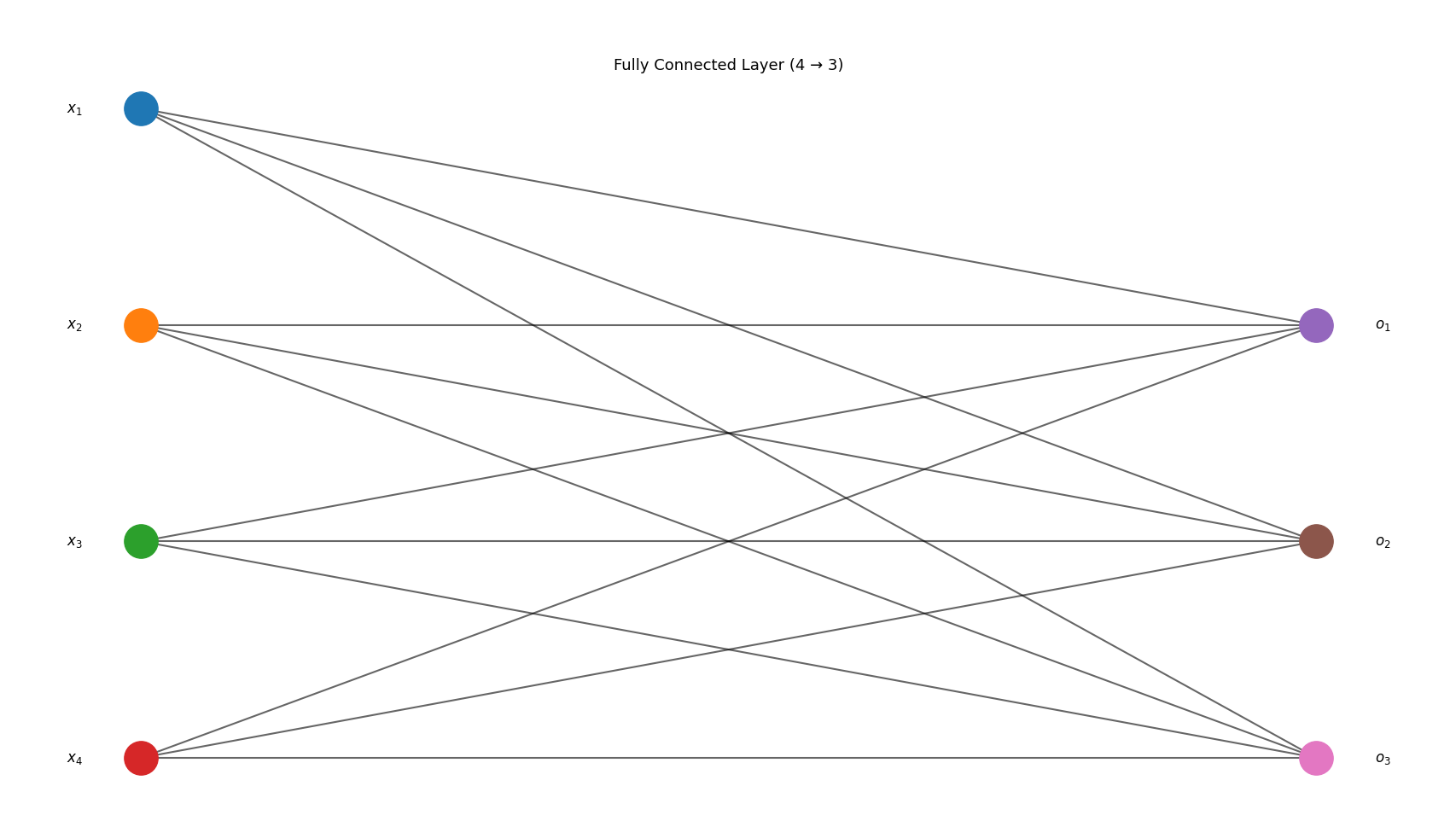
得到的这些结果（\(\{o_i\}\)）都是未规范化的结果（logit）

为了更简洁地表达模型，可以用向量方式表示

\[\mathbf o = \mathbf{Wx} + \mathbf b \]

全连接层的开销

在此之前有全连接层的概念，即每一个输入都与每一个输出连接，从直观上来看是个完全二分图

对于这么一种网络层，计算的开销是\(O(dq)\)的，可以预见计算的消耗很大

但是在训练的过程中可以用某些方式减少这种开销，用超参数\(n\)压缩计算量，使得开销达到\(O(\frac{dq}{n})\)

softmax运算

我们通过一个网络算出来了logit，但是不同类型的问题，logit的大小乃至数量级肯定都无法确定，我们也不想直接参与数值的观察，因此我们需要对于数值规范化，softmax函数就是用来规范化数据的

\[\mathbf {\hat y} = \text{softmax}(\mathbf o) \]

\[\hat {y_j} = \frac{\exp(o_j)}{\sum_k \exp(o_k)} \]

可以发现softmax让logit转化成了一种概率值，所有概率总和是1，并且横向对比下logit越大，softmax值确实越大

尽管softmax是个非线性函数，但是softmax回归的输出仍然有输入特征的仿射变换决定。因此softmax回归依然是个线性模型

小批量样本的向量化

我们通常会针对小批量样本的数据执行向量计算

假设读取了一个批量的样本\(\mathbf X\)，其中特征维度为\(d\)，批量大小为\(n\)，输出中有\(q\)个类别

此时\(\mathbf X \in \mathbb R ^{n \times d}\)，权重\(\mathbf W \in \mathbb R ^{d \times q}\)，偏置\(\mathbf b \in \mathbb R ^{1\times q}\)

softmax的向量表达式便为

\[\mathbf O = \mathbf{XW} + \mathbf b\\ \mathbf{\hat Y} = \text{softmax}(\mathbf O) \]

\(\mathbf X\)中的每一行都是一个样本，softmax运算可以按照行执行，对于\(\mathbf O\)的每一行，我们先对所有项进行幂运算，然后通过求和对它们进行标准化

最终运算结果会经过广播啊，使得\(\mathbf{O}\)和\(\mathbf{\hat Y}\)都是\(\mathbb R^{n\times q}\)

损失函数

接下来采用极大似然估计思考损失函数

softmax得出的结果是个向量\(\mathbf{\hat y}\)，其中每个元素都是输入\(x\)时对应类别的条件概率，也就是

\[\mathbf{\hat y_i} = P(y = A | x) \]

我们假设数据集\(\{ \mathbf{X, Y} \}\)具有\(n\)个样本，其中索引\(i\)的样本由特征向量\(\mathbf{x^{(i)}}\)和独热标签向量\(\mathbf{y^{(i)}}\)组成，则

\[P(\mathbf{Y | X}) = \prod_{i = 1}^n P(\mathbf{y^{(i)} | x^{(i)}}) \]

根据极大似然估计，最大化\(P(\mathbf{Y | X})\)等效于最小化负对数似然

\[-\log P(\mathbf{Y | X}) = \sum_{i = 1}^n l(\mathbf{y^{(i)}, \hat{y}^{(i)}}) \]

其中损失函数为

\[l(\mathbf{y, \hat{y}}) = -\sum_{j = 1}^q y_j\log \hat{y_j} \]

这里的损失函数叫做交叉熵损失（corss-entropy loss）

接下来讨论一下softmax及其导数，利用softmax的定义化一下损失函数

\[\begin{aligned} l(\mathbf{y, \hat y}) &= -\sum_{j = 1}^q y_j \log \frac{\exp(o_j)}{\sum_{k = 1}^q \exp(o_k)} \\ &= \log \sum_{k = 1}^q \exp(o_k) - \sum_{j = 1}^q y_jo_j \end{aligned} \]

（这里可以得知\(\log\)的底数其实是\(e\)）

接下来考虑对logit的偏导

\[\partial_{o_j} l(\mathbf{y, \hat y}) = \text {softmax}(\mathbf o)_j - y_j \]

这下就可以得到对数似然的梯度了

相对于之前均方误差估计，当下问题是分类问题，因而我们用概率向量去处理数据，从而得到交叉熵损失

接下来从信息论角度讨论交叉熵损失

信息论初识

熵是信息论中的核心内容，用于量化数据中的信息

\[H(P) = \sum_j -P(j)\log P(j) \]

可以发现，当我们为一个事物赋予较低的概率时，其信息量反而会更大，即会给人更大的“惊异程度”

这时候再看向交叉熵损失，首先交叉熵从\(P\)到\(Q\)记为\(H(P, Q)\)，想象其代表“主观概率\(Q\)的观察者再看到根据概率\(P\)生成的数据时产生的期望信息量”

当\(P = Q\)时交叉熵达到最小值

也就是说从信息论角度中说，模型的效果越好，其计算出来的loss信息量会越少，从感官角度看，由于模型贴合实际，因而产生的“惊异”信息会变少