【项目】基于链表的任意精度十进制数计算
【项目】基于链表的任意精度十进制数计算
工作流确定
- 编写BigDecimal类,计算须利用链表特性
- 加法:两个平行链表同时移动
- 乘法:两个链表嵌套移动
- 编写Qt前端并打包
- 基础功能:[输入1] op [输入2] = [输出]
- 计算器:字符串输入➡合法性检测➡转化为后缀表达式➡基于栈计算
- 手写表达式计算:YOLO训练出手写识别,接着用计算器的解析器来处理【待定】
BigDecimal类实现
经过开始的试探,我终于探索出了最合适的写法:
只用一个BigDecimal类实现功能
一开始我想着在语义上更加工程化,于是想用下面这种对象链:
Node --> List --> BigDecimal
然后我发现了如果是这样的话,BigDecimal无法任意访问List里面的结点,因此我放弃了这种方式
目前算法侧已经完成了,接下来我将拆开多个主要部分讨论
数据结构的选择
题目要求是链表,但具体是什么链表并没要求,最终我决定用双向链表
首先整理我对链表的需求:
- 能够遍历每一个点
- 可以从前端、后端动态加点
- 每个点都能够修改
其实单向链表也可以做到,但是双向链表可以使得加点操作不论是在前端还是后端都是\(O(1)\)的
同时双向链表本身麻烦的地方在于,如果是中间加点的话,next和prev指针的修改会很麻烦,但是这个场景下没有这个顾虑,因为加点只会在数据的最高位和最低位加
链表部分的基本操作比较好写:
void BigDecimal::popFront() {
if (!head) {
throw std::logic_error("popFront on empty BigDecimal");
}
if (head == tail) {
delete head;
head = tail = nullptr;
return;
}
NodePtr tmp = head;
head = head->next;
head->prev = nullptr;
delete tmp;
}
void BigDecimal::popBack() {
if (!tail) {
throw std::logic_error("popBack on empty BigDecimal");
}
if (head == tail) {
delete tail;
head = tail = nullptr;
return;
}
NodePtr tmp = tail;
tail = tail->prev;
tail->next = nullptr;
delete tmp;
}
void BigDecimal::pushFront(int value) {
if (!head) {
head = new Node(value);
tail = head;
return;
}
NodePtr ins = new Node(value);
head->prev = ins;
ins->next = head;
head = ins;
}
void BigDecimal::pushBack(int value) {
if (!head) {
head = new Node(value);
tail = head;
return;
}
NodePtr ins = new Node(value);
tail->next = ins;
ins->prev = tail;
tail = ins;
}
拷贝方式的考虑
这里先简要分析一下深拷贝和浅拷贝:
- 浅拷贝:复制对象的外层结构,内部引用对象不复制,仍指向同一片内存,修改内部可变对象时,原对象和拷贝对象都会受到影响
- 深拷贝:复制对象的整体结构,递归地复制所有对象,会新开一片内存,修改内部可变对象时,其他对象不受影响
因为要自己写一个类,并且有对应的构造和析构方式,那么内存管理方面要足够上心
在刚开始写的时候我没有考虑这一点,后面在函数参数传递是发生了double free,即同样的内存被多次释放,这就是默认浅拷贝的结果
因此要自主实现深拷贝
BigDecimal::BigDecimal()
: head(nullptr), tail(nullptr), sgn(1), scale(0) {}
BigDecimal::~BigDecimal() {
NodePtr cur = head;
while (cur) {
NodePtr tmp = cur;
cur = cur->next;
delete tmp;
}
head = tail = nullptr;
}
BigDecimal::BigDecimal(const BigDecimal& other)
: head(nullptr), tail(nullptr), sgn(other.sgn), scale(other.scale) {
for (NodePtr cur = other.head; cur; cur = cur->next) {
this->pushBack(cur->value);
}
}
BigDecimal& BigDecimal::operator = (const BigDecimal& other) {
if (this == &other) return *this;
while (head) popFront();
sgn = other.sgn;
scale = other.scale;
for (NodePtr cur = other.head; cur; cur = cur->next) {
this->pushBack(cur->value);
}
return *this;
}
数据的存储形式
小数在某种意义上其实也是整数,我们可以做如下转化
那么用sgn存符号,scale存小数点位数,digit用链表存整数,就可以更加简便地进行运算了
这个时候可以先进行整数的绝对值运算工作
绝对值运算
最终整理出了如下接口
static int getLength(const BigDecimal &X); // 数位长度
static void align(BigDecimal &L, BigDecimal &R); // 小数点前后补零对齐
static bool absGeq(BigDecimal L, BigDecimal R); // 绝对值大小比较
static void mySwap(BigDecimal &L, BigDecimal &R); // 深拷贝下的swap实现
static BigDecimal absAdd(BigDecimal L, BigDecimal R); // 绝对值加法
static BigDecimal absSub(BigDecimal L, BigDecimal R); // 绝对值减法(保证 |L| > |R|)
static是为了让成员函数不与特定对象绑定,原理大概如下
一般的成员函数func()其实是下面的形式:
T func(T* this, ...);
而加入了static后就是:
T func(...);
并且还需要一个到达特定数位长度的函数,用来对存储结果的对象进行初始化,这样就不用计算的过程中动态加点了
void BigDecimal::toTargetLength(int target) {
int cur = getLength(*this);
if (cur > target) {
throw std::logic_error("target length smaller than current length");
}
while (cur < target) {
this->pushBack();
cur++;
}
}
另外计算完之后需要把前导零和后导零去掉,所以就得有个normalize()函数
void BigDecimal::removeFrontZero() {
while (tail && tail->value == 0 && head != tail) {
this->popBack();
}
}
void BigDecimal::removeBackZero() {
while (scale > 0 && head && head->value == 0) {
this->popFront();
scale--;
}
}
void BigDecimal::normalize() {
removeBackZero();
removeFrontZero();
}
接着是剩下的函数实现
int BigDecimal::getLength(const BigDecimal &X) {
int cnt = 0;
NodePtr cur = X.head;
while (cur) {
cnt++;
cur = cur->next;
}
return cnt;
}
void BigDecimal::align(BigDecimal &L, BigDecimal &R) {
if (L.scale < R.scale) {
while (L.scale < R.scale) {
L.pushFront();
L.scale++;
}
}
if (L.scale > R.scale) {
while (L.scale > R.scale) {
R.pushFront();
R.scale++;
}
}
int lenL = getLength(L);
int lenR = getLength(R);
if (lenL < lenR) {
while (lenL < lenR) {
L.pushBack();
lenL++;
}
}
if (lenL > lenR) {
while (lenL > lenR) {
R.pushBack();
lenR++;
}
}
}
void BigDecimal::mySwap(BigDecimal &L, BigDecimal &R) {
BigDecimal tmp = L;
L = R;
R = tmp;
}
bool BigDecimal::absGeq(BigDecimal L, BigDecimal R) {
align(L, R);
int lenL = getLength(L);
int lenR = getLength(R);
if (lenL < lenR) {
return false;
}
if (lenL > lenR) {
return true;
}
NodePtr curL = L.tail;
NodePtr curR = R.tail;
while (curL && curR) {
if (curL->value != curR->value) {
return curL->value > curR->value;
}
curL = curL->prev;
curR = curR->prev;
}
return true;
}
// 加法的实现让长度完全对齐,从而不需要考虑动态加点
BigDecimal BigDecimal::absAdd(BigDecimal L, BigDecimal R) {
align(L, R);
int len = getLength(L);
L.toTargetLength(len + 1);
R.toTargetLength(len + 1);
BigDecimal ret;
ret.toTargetLength(len + 1);
ret.sgn = 1;
ret.scale = L.scale; // L R 此时的scale相同
NodePtr p = L.head, q = R.head;
NodePtr cur = ret.head;
int carry = 0;
while (cur && p && q) {
int value = p->value + q->value + carry;
cur->value = value % 10;
carry = value / 10;
p = p->next;
q = q->next;
cur = cur->next;
}
ret.normalize();
return ret;
}
// 默认 L >= R
BigDecimal BigDecimal::absSub(BigDecimal L, BigDecimal R) {
align(L, R);
BigDecimal ret;
ret.sgn = 1;
ret.scale = L.scale;
int len = getLength(L);
ret.toTargetLength(len);
NodePtr p = L.head, q = R.head;
NodePtr cur = ret.head;
int borrow = 0;
while (cur && p && q) {
int diff = p->value - q->value - borrow;
if (diff < 0) {
diff += 10;
borrow = 1;
} else {
borrow = 0;
}
cur->value = diff;
p = p->next;
q = q->next;
cur = cur->next;
}
ret.normalize();
return ret;
}
加减法运算
首先减法是
A - B = A + (-B)
所以处理好加法的逻辑就好了
分类讨论一下:
- 若A.sgn == B.sgn,那么结果就是
- 若A.sgn != B.sgn,那么结果取决于绝对值较大的数,不妨认为是A,那么结果为
代码就很简单了
BigDecimal BigDecimal::operator + (const BigDecimal &other) {
BigDecimal ret;
if (this->sgn == other.sgn) {
ret = absAdd(*this, other);
ret.sgn = this->sgn;
return ret;
}
if (absGeq(*this, other)) {
ret = absSub(*this, other);
ret.sgn = this->sgn;
} else {
ret = absSub(other, *this);
ret.sgn = other.sgn;
}
return ret;
}
BigDecimal BigDecimal::operator - (const BigDecimal &other) {
BigDecimal neg = other;
neg.sgn = -neg.sgn;
return *this + neg;
}
乘法运算
原理就是竖式乘法,但是需要打破固有的认知
原先做这种大整数题的时候,其实我用vector会下意识地利用随机访问,即
ret[i + j] = A[i] * B[j]
我最开始写了一版也是这样,重载了下标,用随机访问的方式计算,暗地里多了\(O(n)\)复杂度
其实眼界可以更开阔一些,竖式的本质其实是下面这个式子
那么我可以这样做
从而可以计算多个元素相加
\(10^i\)可以通过前端补零的操作实现
这样就是正常的顺序计算,内外两层循环的复杂度都是\(O(n)\),与vector的随机访问策略复杂度一致
小数的加入很简单,用scale相加就是所需的小数位数了
BigDecimal BigDecimal::mulByDigit(int d) {
BigDecimal ret;
ret.sgn = 1;
ret.scale = 0;
int carry = 0;
for (NodePtr cur = this->head; cur; cur = cur->next) {
int value = cur->value * d + carry;
ret.pushBack(value % 10);
carry = value / 10;
}
if (carry) ret.pushBack(carry);
return ret;
}
BigDecimal BigDecimal::operator * (const BigDecimal &other) {
BigDecimal A = *this;
BigDecimal B = other;
BigDecimal ret;
int retSgn = A.sgn * B.sgn;
int retScale = A.scale + B.scale;
A.sgn = B.sgn = 1;
A.scale = B.scale = 0;
int shift = 0;
for (NodePtr cur = B.head; cur; cur = cur->next) {
BigDecimal tmp = A.mulByDigit(cur->value);
for (int i = 0; i < shift; i++)
tmp.pushFront();
ret = absAdd(ret, tmp);
shift++;
}
ret.sgn = retSgn;
ret.scale = retScale;
ret.normalize();
return ret;
}
除法运算
这部分我差点没有转过弯来,其实还是竖式思维
我们考虑用人类的方式思考
做多位数的竖式除法的时候,我们做的事情是从最高位开始一个个确定商的值,并且我们大多数时候都不可能一眼看出对应的商,做的是试除法,其实就是用乘法来验证除法
实现的时候,我们考虑从d=9开始试,对于A / B来说,计算某一位时,我们用\(B \times d\),比较对应余数\(remainder\)和\(B\times d\)的大小
假如\(remainder \geq B \times d\)恰好实现,那么d就是对应位的商值
另外就是小数点后k位的保留策略
在不能整除的情况下,就会产生无限循环小数,那么要做的事情就是固定结果的位数,并且要有四舍五入的效果
一般来讲,如果能整除的话,新的结果\(scale = scale_A - scale_B\)
如果不能整除的话,我们把它当作另一种整数运算,并且忽略余数,我们固定一个\(OUT\_SCALE\),然后让\(A\)左移足够多位,这样就能让商的数位满足保留小数点后k位的要求
四舍五入的做法顺理成章。假设要求保留10位小数,那么我们让结果的位数是小数点后11位,如果第11位大于等于5,那么就让第十位加1
BigDecimal BigDecimal::divInt(BigDecimal A, BigDecimal B) {
BigDecimal quotient;
BigDecimal remainder;
quotient.sgn = 1;
quotient.scale = 0;
remainder.sgn = 1;
remainder.scale = 0;
for (NodePtr cur = A.tail; cur; cur = cur->prev) {
remainder.pushFront(cur->value);
int d = 0;
for (int k = 9; k >= 0; k--) {
BigDecimal tmp = B.mulByDigit(k);
if (absGeq(remainder, tmp)) {
d = k;
remainder = absSub(remainder, tmp);
break;
}
}
quotient.pushFront(d);
}
return quotient;
}
BigDecimal BigDecimal::operator / (const BigDecimal& other) {
BigDecimal A = *this;
BigDecimal B = other;
int retSgn = A.sgn * B.sgn;
A.sgn = B.sgn = 1;
constexpr int TARGET_SCALE = 10;
constexpr int WORK_SCALE = TARGET_SCALE + 1;
int shift = WORK_SCALE + B.scale - A.scale;
if (shift > 0) {
for (int i = 0; i < shift; ++i)
A.pushFront();
}
A.scale = B.scale = 0;
BigDecimal Q = divInt(A, B);
if (Q.head && Q.head->value >= 5) {
BigDecimal inc = convertFromString("1");
inc.pushFront();
Q = absAdd(Q, inc);
}
Q.popFront();
Q.scale = TARGET_SCALE;
Q.sgn = retSgn;
Q.normalize();
return Q;
}
至此算法部分结束
Qt前端设计
整体架构思考
Qt本身是个高度体现C++面向对象特点的工具。我在使用过程中主要用到了其中的两大功能:
- 控件的排版
- 不同类型控件的使用(显示、交互等)
整体开发过程中,我选择了MainWindow作为主要对象,其中用了一个StackedWidget来管理不同的页面
初始页面
作为一开始的页面,我费了很大功夫去实现功能逻辑,最终结果是这样的:
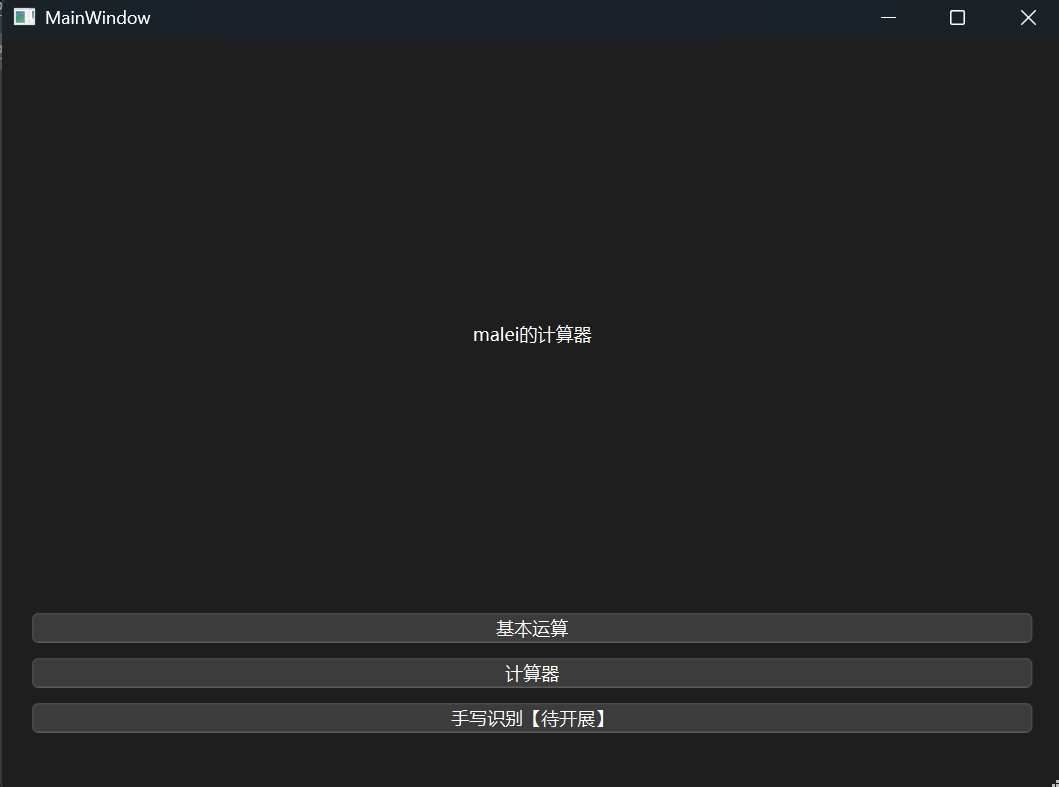
对于整个page采用垂直布局,然后从上到下依次是
[label]
[button]
[button]
[button]
[button]被点击后就会切换到不同的页面
按钮交互涉及到了一个重要的接口:connect,以[基本运算]按钮为例给出代码
connect(ui->btnReturnFromBasic, &QPushButton::clicked, this, [this]() {
ui->stackedWidget->setCurrentWidget(ui->pageInit);
});
这个接口用来绑定对象与其对应的交互逻辑,其中交互逻辑可以用lambda简单实现
就底层含义来讲,内容如下:
connect(sender, signal, receiver, slot)
分别代表信号发出者、触发的信号、接收者对象、响应函数
其中lambda的结构有必要细讲一下
[捕获列表] (参数表) { 函数体 }
捕获列表代表的是函数体内能够使用的外部对象,捕获列表有一些特殊的使用方式:
[this] // 捕获当前对象
[=] // 以值传递的方式捕获所有外部对象
[&] // 以引用传递的方式捕获所有外部对象
在connect函数中,lambda的参数表只能源自于signal的参数表
基本运算界面
首先给出效果
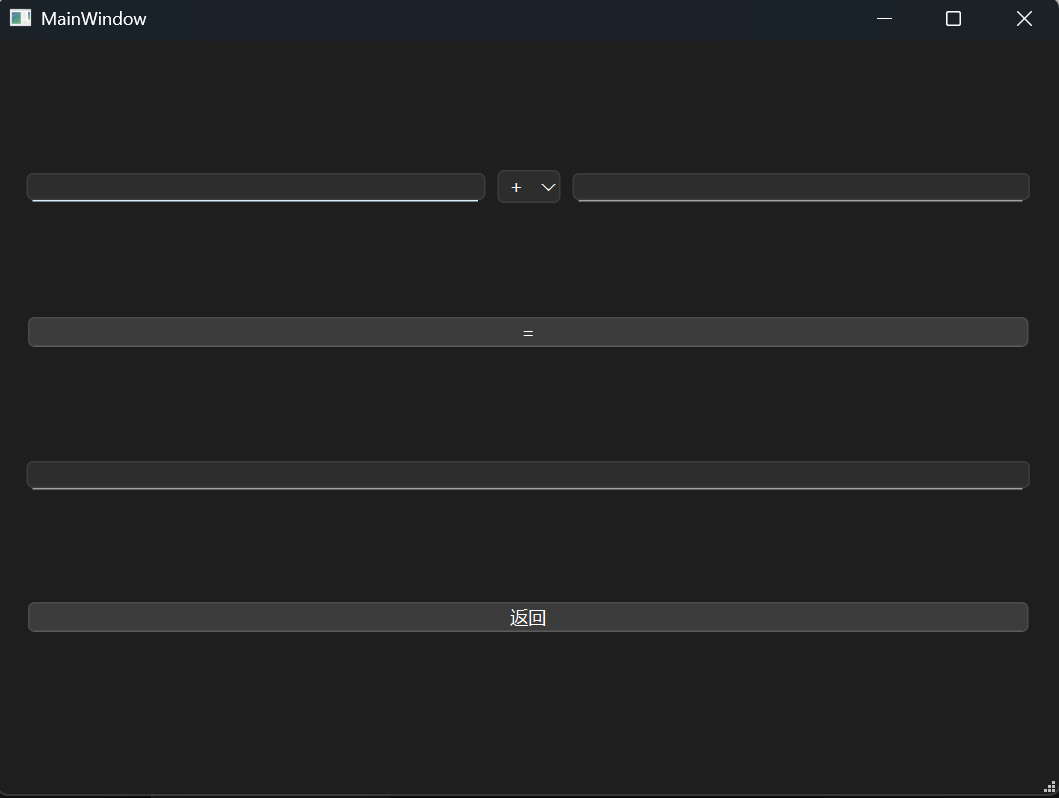
是个垂直布局,第一行嵌套了个水平布局,结构为
[line edit] [combo box] [line edit]
[button]
[line edit (read only)]
[button]
[line edit]组件很直观,就是字符串的输入输出显示的地方,这个地方的字符串类型是QString,不过Qt自身支持QString和string类的互相转换,所以实现好string类的函数就行了
[combo box]在这里用于承载运算符号,顾名思义可以有多种选项
等于号对应的button被点击时就要进行计算,操作如下:
connect(ui->btnEqual, &QPushButton::clicked, this, [this]() {
QString s = ui->editA->text();
QString t = ui->editB->text();
QString op = ui->opBox->currentText();
if (s.isEmpty() || t.isEmpty()) return;
std::string result = CalculatorEngine::calc(
s.toStdString(),
t.toStdString(),
op[0].toLatin1());
ui->editResult->setText(QString::fromStdString(result));
});
其中CalculatorEngine是个另外实现的类,用于简单的计算操作,在这里也给出接口和实现
#pragma once
#include <string>
class CalculatorEngine {
public:
static std::string calc(const std::string &s, const std::string &t, char op);
};
#include "CalculatorEngine.h"
#include "BigDecimal.h"
std::string CalculatorEngine::calc(
const std::string &s,
const std::string &t,
char op) {
BigDecimal A = BigDecimal::convertFromString(s);
BigDecimal B = BigDecimal::convertFromString(t);
switch (op) {
case '+': return (A + B).convertToString();
case '-': return (A - B).convertToString();
case '*': return (A * B).convertToString();
case '/': return (A / B).convertToString();
default: return "ERR";
}
}
最后就是下面这样
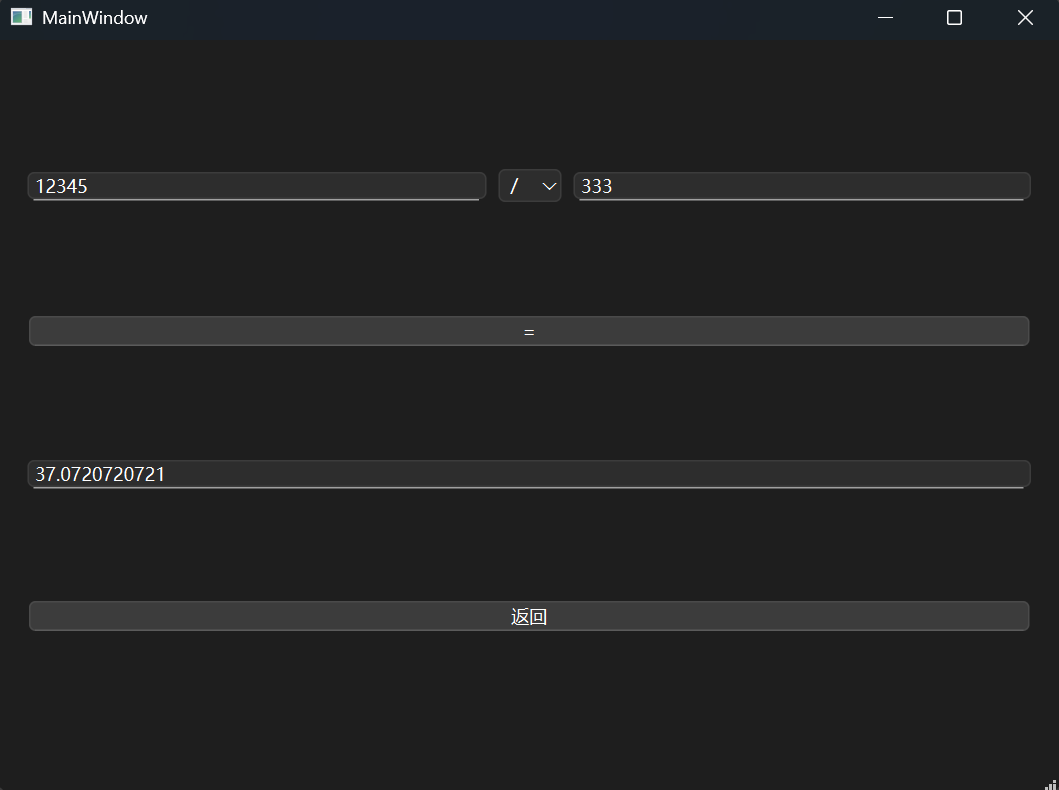
简单运算的界面到这里就基本没有难点了
计算器键盘实现
我设想的是模仿现行的计算器软件,因而我试着做了个虚拟键盘,做成了下面这样
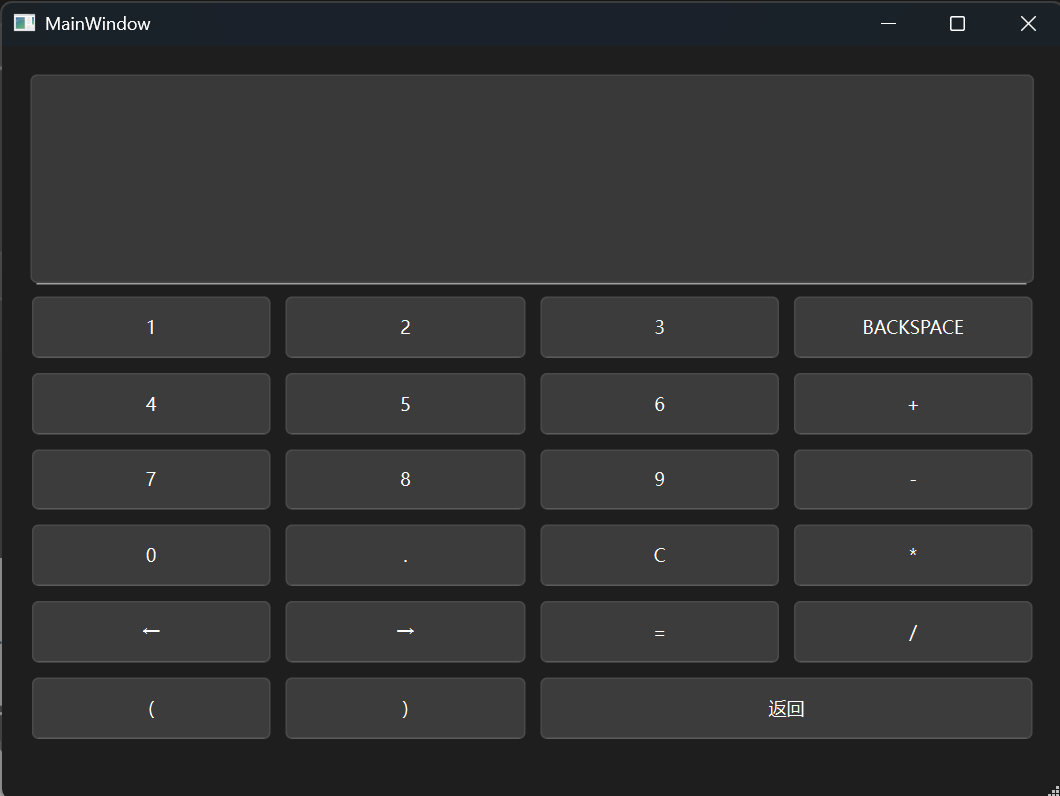
这时候用了一个新类型的布局方式:栅格布局
其实就是个同时支持水平布局和垂直布局的布局方式,在这里我希望让按钮填满表格,所以就在sizePolicy处把水平和垂直策略调成了Expanding,最终看起来不错
这个键盘实际上就是实际键盘的映射,并且line edit组件本身就是允许键盘输入的,因此把按钮依次映射到对应的键位就可以成为一个简单的文本编辑器了
由于界面不是很多,我直接在MainWindow类加了一些函数,实现如下:
void MainWindow::calcInsert(const QString &text) {
ui->editArea->setFocus();
ui->editArea->insert(text);
}
void MainWindow::calcBackspace() {
ui->editArea->backspace();
}
void MainWindow::calcClear() {
ui->editArea->clear();
}
void MainWindow::calcMoveCursorLeft() {
ui->editArea->setFocus();
int pos = ui->editArea->cursorPosition();
if (pos > 0) {
ui->editArea->setCursorPosition(pos - 1);
}
}
void MainWindow::calcMoveCursorRight() {
ui->editArea->setFocus();
int pos = ui->editArea->cursorPosition();
if (pos < ui->editArea->text().length()) {
ui->editArea->setCursorPosition(pos + 1);
}
}
void MainWindow::setupCalculatorConnections() {
QVector<QPushButton*> digitButtons = {
ui->btn0, ui->btn1, ui->btn2, ui->btn3, ui->btn4, ui->btn5, ui->btn6, ui->btn7, ui->btn8, ui->btn9
};
for (auto btn : digitButtons) {
connect(btn, &QPushButton::clicked, this, [this, btn]() {
calcInsert(btn->text());
});
}
QVector<QPushButton*> opButtons = {
ui->btnAdd, ui->btnSub, ui->btnMul, ui->btnDiv, ui->btnDot, ui->btnLBrac, ui->btnRbrac
};
for (auto btn : opButtons) {
connect(btn, &QPushButton::clicked, this, [this, btn]() {
calcInsert(btn->text());
});
}
connect(ui->btnBack, &QPushButton::clicked, this, &MainWindow::calcBackspace);
connect(ui->btnClear, &QPushButton::clicked, this, &MainWindow::calcClear);
connect(ui->btnLeft, &QPushButton::clicked, this, &MainWindow::calcMoveCursorLeft);
connect(ui->btnRight, &QPushButton::clicked, this, &MainWindow::calcMoveCursorRight);
connect(ui->btnReturnFromCalc, &QPushButton::clicked, this, [this]() {
ui->stackedWidget->setCurrentWidget(ui->pageInit);
});
}
一开始我还比较纳闷为什么我实现左右移动光标了,但是光标没有被高亮
后面才知道要让光标高亮需要让focus一直放在最上面的line edit,所以在插入、左右移动光标的时候都加一个setFocus就行了
最后是等于号按钮的逻辑,用下文写出来的接口直接计算就可以了
void MainWindow::onEqualClicked() {
ExpressionEvaluator evaluator;
BigDecimal result = evaluator.evaluate(ui->editArea->text().toStdString());
QString output = QString::fromStdString(result.convertToString());
output.remove(',');
ui->editArea->setText(output);
ui->editArea->setCursorPosition(output.length());
}
表达式求值
这本来是在计算器界面下的内容,但这个部分涉及的东西甚至比界面多,所以就单开了一个二级标题
Token化
对于一个表达式,首先要让计算机能够“看出”它是什么,比如下面这个算式
-3+4*(5-6)
单元运算符需要另外处理,整个表达式处理成:
NEG 3 + 4 * ( 5 - 6 )
再进行一级分类:
OP NUM OP NUM OP LBRAC NUM OP NUM RBRAC
于是表达式中的元素可以被划分成以上的四种token进行处理
实现中先写个Token.h
#pragma once
#include <string>
enum class TokenType {
Number,
Operator,
LeftBrac,
RightBrac
};
struct Token {
TokenType type;
std::string text;
};
接下来就是把表达式化成Token序列,其实就是个字符串处理
#pragma once
#include <vector>
#include <string>
#include "Token.h"
class Tokenizer {
public:
std::vector<Token> tokenize(const std::string &expr);
};
#include <cctype>
#include "Tokenizer.h"
std::vector<Token> Tokenizer::tokenize(const std::string &expr) {
std::vector<Token> tokens;
size_t i = 0;
auto prevIsOperatorOrLeftBrac = [&]() {
if (tokens.empty()) return true;
auto t = tokens.back().type;
return t == TokenType::Operator || t == TokenType::LeftBrac;
};
while (i < expr.size()) {
char c = expr[i];
if (std::isspace(c)) {
i++;
continue;
}
if (std::isdigit(c) || c == '.') {
size_t start = i;
while (i < expr.size() && (std::isdigit(expr[i]) || expr[i] == '.')) {
i++;
}
tokens.push_back({TokenType::Number, expr.substr(start, i - start)});
continue;
}
if (c == '(') {
tokens.push_back({TokenType::LeftBrac, "("});
i++;
continue;
}
if (c == ')') {
tokens.push_back({TokenType::RightBrac, ")"});
i++;
continue;
}
if (c == '-' && prevIsOperatorOrLeftBrac()) {
tokens.push_back({TokenType::Operator, "NEG"});
} else {
tokens.push_back({TokenType::Operator, std::string(1, c)});
}
i++;
}
return tokens;
}
化为后缀表达式
后缀(逆波兰)表达式可以用栈模拟,更有利于表达式计算
因此输入的中缀表达式需要转化为后缀表达式
由于不同的运算符有不同的优先级,因此先写个OperatorTable.h来对应不同运算符的基本信息
#pragma once
#include <string>
#include <unordered_map>
struct OperatorInfo {
int precedence; // 优先级
bool rightAssociative; // 是否右关联
int arity; // 运算符目数
};
class OperatorTable {
private:
static const std::unordered_map<std::string, OperatorInfo> table;
public:
static const OperatorInfo& get(const std::string &op);
static bool isOperator(const std::string &op);
};
#include "OperatorTable.h"
const std::unordered_map<std::string, OperatorInfo> OperatorTable::table = {
{"+", { 1, false, 2 }},
{"-", { 1, false, 2 }},
{"*", { 2, false, 2 }},
{"/", { 2, false, 2 }},
{"NEG", { 3, true, 1 }}
};
const OperatorInfo& OperatorTable::get(const std::string &op) {
return table.at(op);
}
bool OperatorTable::isOperator(const std::string &op) {
return table.count(op) > 0;
}
后面就是转化为后缀表达式,利用Shunting-Yard算法
首先数字的相对顺序是不会改变的,要处理的只是运算符出现的时机
实现的过程中,我们维护两个东西:输出token数组output,符号栈opStack
扫描整个token序列,如果是数就直接放进output
否则把当前扫到的符号与栈顶符号比较,对于这里全都是左结合运算符来说,若当前优先级≤栈顶优先级就需要先算栈顶,比如:
3 - 2 + 1
就要保证是
(3 - 2) + 1
接着是括号的问题,遇到左括号放进栈顶,直到碰到右括号,这个时候触发清算过程,类似在递归地处理一个表达式单元,这个时候直接把符号全都弹出来就好了,弹完之后再把左括号去掉
最后还需要把还处于栈内的运算符全部弹出来
#pragma once
#include <vector>
#include "Token.h"
class ShuntingYard {
public:
std::vector<Token> toRpn(const std::vector<Token> &infix);
};
#include <stack>
#include "ShuntingYard.h"
#include "OperatorTable.h"
std::vector<Token> ShuntingYard::toRpn(const std::vector<Token> &infix) {
std::vector<Token> output;
std::stack<Token> opStack;
for (const auto &tok : infix) {
if (tok.type == TokenType::Number) {
output.push_back(tok);
}
else if (tok.type == TokenType::Operator) {
const auto &op1 = OperatorTable::get(tok.text);
while (!opStack.empty() &&
opStack.top().type == TokenType::Operator) {
const auto &op2 =
OperatorTable::get(opStack.top().text);
bool pop =
(!op1.rightAssociative && op1.precedence <= op2.precedence) ||
( op1.rightAssociative && op1.precedence < op2.precedence);
if (!pop) break;
output.push_back(opStack.top());
opStack.pop();
}
opStack.push(tok);
}
else if (tok.type == TokenType::LeftBrac) {
// 左括号:直接压栈
opStack.push(tok);
}
else if (tok.type == TokenType::RightBrac) {
// 右括号:弹到左括号
while (!opStack.empty() &&
opStack.top().type != TokenType::LeftBrac) {
output.push_back(opStack.top());
opStack.pop();
}
// 丢弃左括号
if (!opStack.empty() &&
opStack.top().type == TokenType::LeftBrac) {
opStack.pop();
}
}
}
while (!opStack.empty()) {
output.push_back(opStack.top());
opStack.pop();
}
return output;
}
后缀表达式求值
拿个栈存储运算过程的数,碰到符号就把栈顶数据拿出来算
其中负号NEG需要特别处理,拿出栈顶元素算个0 - NUM就好了
#pragma once
#include <vector>
#include "Token.h"
#include "BigDecimal.h"
class RpnEvaluator {
public:
BigDecimal evaluate(const std::vector<Token> &rpn);
};
#include <stack>
#include "RpnEvaluator.h"
#include "OperatorTable.h"
BigDecimal RpnEvaluator::evaluate(const std::vector<Token> &rpn) {
std::stack<BigDecimal> st;
for (const auto &tok : rpn) {
if (tok.type == TokenType::Number) {
st.push(BigDecimal::convertFromString(tok.text));
} else {
const auto &info = OperatorTable::get(tok.text);
if (info.arity == 1) {
BigDecimal a = st.top(); st.pop();
BigDecimal zero = BigDecimal::convertFromString("0");
st.push(zero - a);
} else {
BigDecimal b = st.top(); st.pop();
BigDecimal a = st.top(); st.pop();
if (tok.text == "+") st.push(a + b);
else if (tok.text == "-") st.push(a - b);
else if (tok.text == "*") st.push(a * b);
else if (tok.text == "/") st.push(a / b);
}
}
}
return st.top();
}
封装
设计一个仅输入string输出BigDecimal的接口,便于Qt调用
#pragma once
#include <string>
#include "BigDecimal.h"
class ExpressionEvaluator {
public:
BigDecimal evaluate(const std::string &expr);
};
#include "ExpressionEvaluator.h"
#include "Tokenizer.h"
#include "ShuntingYard.h"
#include "RpnEvaluator.h"
BigDecimal ExpressionEvaluator::evaluate(const std::string &expr) {
Tokenizer tokenizer;
ShuntingYard shuntingYard;
RpnEvaluator rpnEvaluator;
auto tokens = tokenizer.tokenize(expr);
auto rpn = shuntingYard.toRpn(tokens);
return rpnEvaluator.evaluate(rpn);
}
细节处理
输入限制
用到正则表达式,限制只能输入数字和特定符号
涉及到了QRegularExpression类
QRegularExpression re("[0-9+\\-*/().]*");
ui->editArea->setValidator(new QRegularExpressionValidator(re, this));
ui->editA->setValidator(new QRegularExpressionValidator(re, this));
ui->editB->setValidator(new QRegularExpressionValidator(re, this));
合法性判断
其实输入的表达式不一定是合法的,因此要在确定合法之后再计算,否则可能导致程序崩溃
主要的思路是Tokenize之后再进行一些初步判断,包含:
- 空表达式
- 起始、结尾、相邻Token合法性
- 括号匹配
- 运算符语义(一元、二元)
- RPN可归约性(是否可算)
为了更加系统化地处理这个事情,考虑构造一个Validator对象
首先列出不同的错误类型:
enum class ValidationError {
None,
EmptyExpression,
InvalidTokenSequence,
MisMatchedParentheses,
OperatorMisuse,
OperandMissing,
NotReducible
};
这里再次用到了enum class,简要强调一下
enum class强制地隐藏了作为数的特征,只保留了语义上的特点,在使用时会更加集中于语义
接着用一个结构体保存错误信息
struct ValidationResult {
bool ok;
ValidationError error;
int errorPos;
std::string message;
};
接下来就是Validator的一些接口
typedef std::vector<Token>& TokenVecRef;
class Validator {
private:
static ValidationResult checkEmpty(const TokenVecRef tokens);
static ValidationResult checkSequence(const TokenVecRef tokens);
static ValidationResult checkParentheses(const TokenVecRef tokens);
static ValidationResult checkOperatorSemantics(const TokenVecRef tokens);
static ValidationResult checkReducible(TokenVecRef tokens);
static bool isValidTransition(TokenType prev, TokenType curr);
static bool isUnaryPosition(const TokenVecRef tokens, size_t i);
static bool isRpnValid(const TokenVecRef rpn);
public:
static ValidationResult validate(const TokenVecRef tokens);
};
统一的合法性接口没有什么好说的,不过用到了function<T(...)>这个好用的函数变量对象,在C++中可以有效取代函数指针
#define OK { true, ValidationError::None, -1, "" };
// 统一合法性接口
ValidationResult Validator::validate(const TokenVecRef tokens) {
ValidationResult r;
vector<function<ValidationResult(const TokenVecRef)>> checkFuncs = {
checkEmpty,
checkSequence,
checkParentheses,
checkOperatorSemantics,
checkReducible
};
for (auto func : checkFuncs) {
r = func(tokens);
if (!r.ok) return r;
}
return OK;
}
简单的合法性判断如下:
// 空表达式
ValidationResult Validator::checkEmpty(const TokenVecRef tokens) {
if (tokens.empty())
return { false, ValidationError::EmptyExpression, -1, "Expression is Empty" };
return OK;
}
// 相邻Token合法性
bool Validator::isValidTransition(TokenType prev, TokenType curr) {
using T = TokenType;
if (prev == T::Number && (curr == T::Number || curr == T::LeftBrac))
return false;
if (prev == T::Operator && (curr == T::Operator || curr == T::RightBrac))
return false;
if (prev == T::LeftBrac && curr == T::RightBrac)
return false;
if (prev == T::RightBrac && (curr == T::Number || curr == T::LeftBrac))
return false;
return true;
}
ValidationResult Validator::checkSequence(const TokenVecRef tokens) {
TokenType t;
// 起始Token合法性
t = tokens.front().type;
if (!(t == TokenType::Number||
t == TokenType::LeftBrac ||
t == TokenType::Operator)) {
return { false, ValidationError::InvalidTokenSequence, 0, "Invalid start of expression" };
}
// 结尾Token合法性
t = tokens.back().type;
if (!(t == TokenType::Number ||
t == TokenType::RightBrac)) {
return { false, ValidationError::InvalidTokenSequence, (int)tokens.size() - 1, "Invalid end of expression" };
}
// 中间相邻Token合法性
for (size_t i = 1; i < tokens.size(); i++) {
if (!isValidTransition(tokens[i - 1].type, tokens[i].type)) {
return { false, ValidationError::InvalidTokenSequence, (int)i, "Invalid token sequence" };
}
}
return OK;
}
接着是括号匹配,其实就是一个抵消的规律,设置一个变量(或栈),左括号出现时入栈,右括号出现时出栈,如果最后恰好全部抵消就是匹配成功
// 括号匹配
ValidationResult Validator::checkParentheses(const TokenVecRef tokens) {
int balance = 0;
for (size_t i = 0; i < tokens.size(); i++) {
if (tokens[i].type == TokenType::LeftBrac)
balance++;
else if (tokens[i].type == TokenType::RightBrac)
balance--;
if (balance < 0)
return { false, ValidationError::MisMatchedParentheses, (int)i, "Extra ')'" };
}
if (balance != 0)
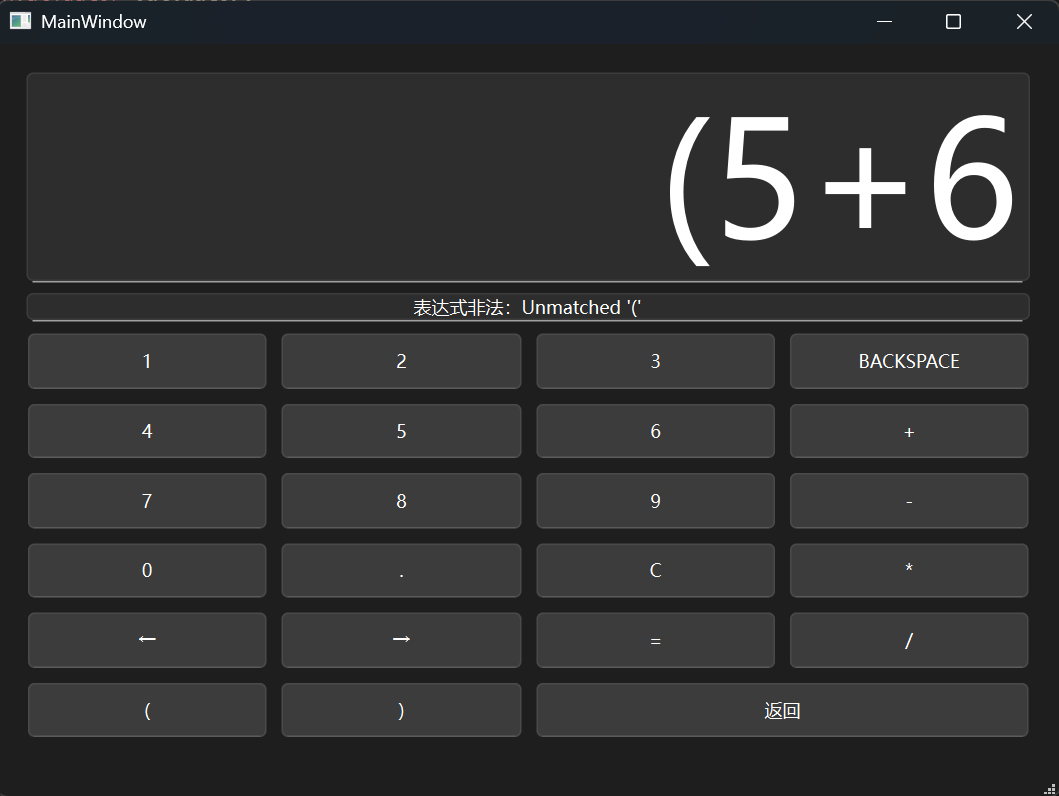
return { false, ValidationError::MisMatchedParentheses, -1, "Unmatched '('"};
return OK;
}
下面是运算符语义的考虑,主要是区分一元运算符和二元运算符,不过这时候暴露了一个问题,我一开始没考虑到一元加号的问题,不过在使用的时候问题不会很大
// 运算符语义
bool Validator::isUnaryPosition(const TokenVecRef tokens, size_t i) {
if (i == 0) return true;
auto prev = tokens[i - 1].type;
return prev == TokenType::Operator || prev == TokenType::LeftBrac;
}
ValidationResult Validator::checkOperatorSemantics(const TokenVecRef tokens) {
using T = TokenType;
for (size_t i = 0; i < tokens.size(); i++) {
if (tokens[i].type != T::Operator) continue;
bool unary = isUnaryPosition(tokens, i);
if (unary) {
if (i + 1 >= tokens.size())
return { false, ValidationError::OperandMissing, (int)i, "Missing operand after unary operator" };
auto next = tokens[i + 1].type;
if (!(next == T::Number || next == T::LeftBrac))
return { false, ValidationError::OperatorMisuse, (int)i, "Invalid unary operator usage" };
} else {
if (i + 1 >= tokens.size())
return { false, ValidationError::OperandMissing, (int)i, "Missing right operand" };
auto next = tokens[i + 1].type;
if (!(next == T::Number || next == T::LeftBrac))
return { false, ValidationError::OperandMissing, (int)i, "Invalid right operand" };
}
}
return OK;
}
最后一道防线是试着RPN计算,如果出现问题立刻停止
// RPN可归约性
bool Validator::isRpnValid(const TokenVecRef rpn) {
int stack = 0;
for (const auto &tok : rpn) {
if (tok.type == TokenType::Number) {
stack++;
} else if (tok.type == TokenType::Operator) {
OperatorInfo op = OperatorTable::get(tok.text);
int need = op.arity;
if (stack < need) return false;
stack -= need;
stack++;
}
}
return stack == 1;
}
ValidationResult Validator::checkReducible(const TokenVecRef tokens) {
try {
ShuntingYard SY;
auto rpn = SY.toRpn(tokens);
if (!isRpnValid(rpn))
return { false, ValidationError::NotReducible, -1, "Expression is not reducible" };
} catch (...) {
return { false, ValidationError::NotReducible, -1, "Expression is not reducible" };
}
return OK;
}
接着再封装成打包即用的接口
#pragma once
#include <string>
#include "BigDecimal.h"
class ExpressionEvaluator {
public:
BigDecimal evaluate(const std::string &expr);
};
#include "ExpressionValidator.h"
ValidationResult ExpressionValidator::validate(const std::string &expr) {
Tokenizer tokenizer;
auto tokens = tokenizer.tokenize(expr);
auto result = Validator::validate(tokens);
return result;
}
实际计算中发现rpn可归约性几乎到达不了(
现在回到Qt,由于此前已经正则规定了输入框的字符集,语义上还是不在输入框输出状态比较好,所以需要另开一个label记录信息
到这里注意到了Qt的报错信息,原来我之前的typedef是不对的
我把const vector< Token >& 变成了const vecTokenRef,这样只能说明vector< Token >对象不会被改变,但是其内部还是能被修改的,和我要求的语义不一样
但是在实现中我没修改过vector< Token >,所以把const 去掉得了
接着就是在等于按钮里面加上校验的逻辑,效果如下:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号