【d2l】3.1.线性回归

【d2l】3.1.线性回归

线性回归的基本元素

• 数据集/训练集
• 数据样本/数据点/数据实例
• 标签/目标
• 特征/协变量
• 表示方式
  • 输入：\(x^{(i)} = [x_1^{(i)}, x_2^{(i)}]^\top\)
  • 标签：\(y^{(i)}\)

线性模型：如何建模

接下来引入一个房屋价格预测作为例子

线性假设是指目标（房屋价格）可以表示为特征（面积和房龄）的加权和，如下：

\[price = w_{area} \cdot area + w_{age} \cdot age + b \]

• \(w\)：权重，决定了每个特征对预测值的影响
• \(b\)：偏置，所有特征值都为\(0\)时应有的取值，为了提高模型的表达能力
• 从线性代数的角度看，这个操作是对输入进行了仿射变换

而在机器学习中一般采用的是高维数据集，因而用线性代数表示法会更加方便

首先对于\(d\)个特征值，原本的\(\hat y\)应该是

\[\hat y = w_1x_1 + ... + w_dx_d + b \]

将特征和权重分别放在对应的向量中可得

\[\hat y = \mathbf{w^\top x} + b \]

对于特征集合，预测值向量可表示为

\[\mathbf{\hat y} = \mathbf{Xw} + b \]

这个过程中的求和会采用广播机制

另外为了提高模型的灵活性，一般即便确信特征值与标签的潜在关系是线性的，也会去加入一个噪声项考虑观测误差带来的影响

目前表示法已经确定，但还有两件事情需要解决：

• 如何度量一个模型的质量
• 如何更新模型以提高模型质量

损失函数：如何度量模型质量

损失函数（loss function）用于量化目标的实际值和观测值之间的差距

一般而言损失函数需要是非负值，绝对值越小表示与现实的差距越小

平方误差可以如下定义

\[l^{(i)}(\mathbf{w}, b) = \frac 1 2 (\hat y ^{(i)} - y^{(i)})^2 \]

这个损失函数在后续就可以知道是个重要的反向传播载体，因而\(\frac 1 2\)的系数可以让导数系数为\(1\)，让形式稍微简单一些

由于平方项受偏移影响程度较大，操作时会对多个样本的平方误差求均值

\[L(\mathbf{w}, b) = \frac 1 n \sum_{i = 1}^n l^{(i)}(\mathbf{w}, b) = \frac 1 n \sum_{i = 1}^n \frac 1 2 (\mathbf{w^\top x}^{(i)} + b - y^{(i)})^2 \]

训练模型时，我们的目标就是找到使得损失最小的\((\mathbf{w}^*, b^*)\)，即

\[\mathbf{w}^*, b^* = \arg \min_{\mathbf{w}, b}L(\mathbf{w}, b) \]

解析解与随机梯度下降：如何得到最优模型

对于线性模型来讲，是有可能得到随机解的，由于我们的目标是最小化

\[||\mathbf{y - Xw}||^2 \]

因而我们令这个式子对于\(\mathbf{w}\)的导数为\(0\)，可以得到

\[\mathbf{w}^* = \mathbf{(X^\top X)^{-1}X^\top y} \]

但是相当多的情况都是得不到解析解的，因此需要利用一些计算上的方式

本书中采用的方式是“梯度下降”，更具体地说，是“小批量随机梯度下降”

在每次迭代中，随机抽取一个小批量\(B\)，由固定数量的训练样本组成，对于这个小批量样本计算损失函数的梯度，接着将梯度乘上预先确定的正数\(\eta\)，并从当前参数的值中被减掉

具体上看，就是向着梯度方向按着一定的尺度移动

\[(\mathbf w, b) \leftarrow (\mathbf w, b) - \frac{\eta}{|B|}\sum_{i \in b}\partial_{\mathbf w, b}l^{(i)}(\mathbf w, b) \]

在深度优先中，这些参数都有自己的名字

• \(\eta\)：学习率（learning rate）
• \(|B|\)：批量大小（batch size）
• 超参数：可以调整但不在训练过程中更新的参数

在训练了若干次迭代后，我们可以得到估计值\((\mathbf{\hat w},\hat b)\)，但一般情况下这些估计值并不能真正地使得损失函数达到最小值，因为随着训练的进行，算法会使损失缓慢收敛

对于一个算法，最终目标是做到“泛化”，即让一组模型在完全没见过的数据集中达到良好的预测效果（得到较小的损失）

向量化加速

这一部分主要展示向量化对于效率的影响

首先在d2l local中定义一个计时器类

class Timer:
    """记录多次运行时间"""

    def __init__(self):
        self.times = []
        self.start()
    
    def start(self):
        """启动计时器"""
        self.tik = time.time()
    
    def stop(self):
        """停止计时器并将时间记录在表中"""
        self.times.append(time.time() - self.tik)
        return self.times[-1]
    
    def avg(self):
        """返回平均时间"""
        return sum(self.times) / len(self.times)
    
    def sum(self):
        """返回时间总和"""
        return sum(self.times)
    
    def cumsum(self):
        """返回累计时间"""
        return np.array(self.times).cumsum().tolist()

接着分别计算遍历加法和向量加法的时间

n = 10000
a = torch.ones(n)
b = torch.ones(n)

c = torch.zeros(n)
timer = d2l.Timer()
for i in range(n):
    c[i] = a[i] + b[i]
f'{timer.stop() : .5f} sec'

timer.start()
d = a + b
f'{timer.stop() : .5f} sec'

得到的结果差距很明显

' 0.06807 sec'

' 0.00000 sec'

正态分布与平方损失

正态分布是这个式子：

\[p(x) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp[-\frac{1}{2\sigma^2}(x - \mu)^2] \]

用python来算一下正态分布并可视化

def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma**2)
    return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

x = np.arange(-7, 7, 0.01)

params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params],
         xlabel = 'x', ylabel = 'p(x)', figsize = (4.5, 2.5),
         legend = [f'mean {mu}, std {sigma}' for mu, sigma in params])

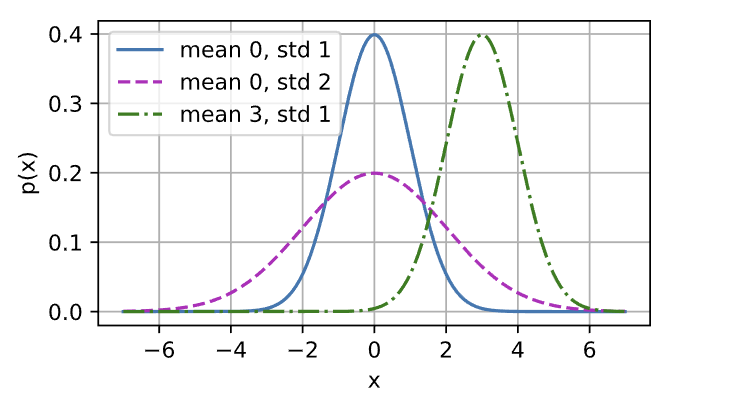
正态分布主要有两个几何特点：

• 改变均值会产生沿x轴的偏移
• 增加方差会分散分布，降低峰值

均方误差损失函数（均方损失）可以用于线性回归，其原因便是假设观测中包含噪声，这个噪声服从正态分布，即

\[y = \mathbf{w^\top x} + b +\epsilon \]

\(\epsilon \sim N(0, \sigma^2)\)

因此，我们现在可以写出通过给定的\(x\)观测到特定\(y\)的似然（likelihood）

\[p(y | \mathbf x) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp[-\frac{1}{2\sigma^2}(y - \mathbf{w^\top x}- b)^2] \]

关于似然的理解，其实是对于参数“合理程度”的评估

目前对于\(\mathbf x\)和\(y\)都已经存在，我们需要评估参数\((\mathbf w, b, \sigma)\)的合理程度

通过极大似然估计法，参数\(\mathbf w\)和\(b\)的最优值是使得整个数据集的似然最大的值

\[P(\mathbf y, \mathbf X) = \prod_{i = 1}^n p(y^{(i)} | \mathbf x^{(i)}) \]

乘积在计算上比较困难，因此可以取对数变成加法

并且由于历史原因，我们的优化目标是极小化似然，因此采用了最小化负对数似然

\[-\log P(\mathbf y | \mathbf X) = \sum_{i = 1}^n [\frac 1 2 \log(2\pi \sigma ^2) + \frac 1 {2\sigma^2}(y^{(i)} - \mathbf{w^\top x}^{(i)} - b)^2] \]

现在只要假设\(\sigma\)是某一个固定常熟就可以忽略第一项，第二项除了常数系数之外与前面的均方误差一致

至此，我们完成了高斯噪声对于均方误差等价性的讨论