【d2l】2.6.概率

【d2l】2.6.概率

本节的代码量比较小，主要在于构建一个对于概率的观念

大数定律

这个部分利用脚本来验证大数定律

先导入所需要的库

%matplotlib inline
import torch
from torch.distributions import multinomial

import sys
sys.path.append("..")
from d2l_local import torch as d2l

然后尝试使用一下Multinomial()函数

fair_probs = torch.ones([6]) / 6

multinomial.Multinomial(1, fair_probs).sample()

multinomial.Multinomial(10, fair_probs).sample()

counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000

tensor([0., 1., 0., 0., 0., 0.])
tensor([2., 1., 1., 2., 1., 3.])
tensor([0.1460, 0.1670, 0.1720, 0.1780, 0.1570, 0.1800])

Multinomial()函数是对于离散选择的一种分布，即多项分布（multinomiak distribution）

接下来绘图看看大数定律的可视化形式

counts = multinomial.Multinomial(10, fair_probs).sample((500, ))
cum_counts = counts.cumsum(dim = 0)
estimates = cum_counts / cum_counts.sum(dim = 1, keepdims = True)

d2l.set_figsize((6, 4.5))

for i in range(6):
    d2l.plt.plot(estimates[:, i].numpy(),
                 label = (f'P(die = {str(i + 1)})'),
                 alpha = 0.7)

d2l.plt.axhline(y = 0.167, color = 'black', linestyle = 'dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')

d2l.plt.legend()

首先前三个语句比较有说法

counts = multinomial.Multinomial(10, fair_probs).sample((500, ))

每一次抽样十个，但是进行五百组，可以逐步看到变化

cum_counts = counts.cumsum(dim = 0)

联动前面的内容，这是在求前缀和，这也说明了独立的概率与是否在同一组不相关

estimates = cum_counts / cum_counts.sum(dim = 1, keepdims = True)

这一句就是在计算频率进而估计概率了

结果如下

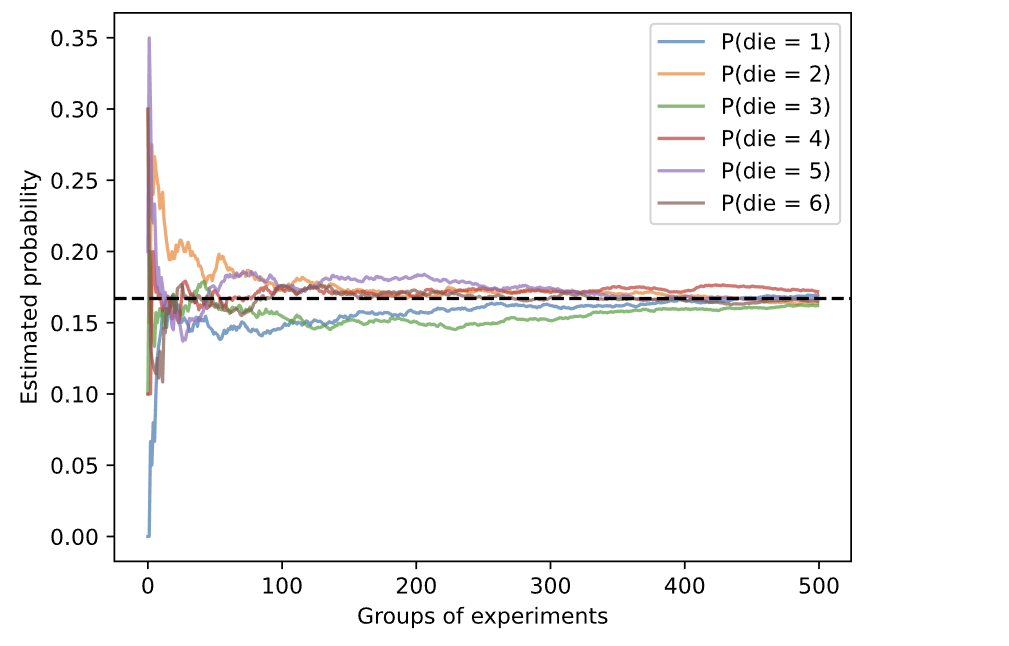
处理多个随机变量

主要涉及下面几种内容

• 联合概率：\(P(A = a, B = b)\)

• 条件概率：

  \[0 \leq \frac{P(A = a, B = b)}{P(A = a)} \leq 1 \]

• 贝叶斯定理：

\[P(A | B) = \frac{P(B | A)P(A)}{P(B)} \]

• 边际化：利用求和法则将联合概率聚合到一起

\[P(B) = \sum_{A}P(A, B) \]

• 独立性

期望和方差

这一块是用来概括概率分布的关键特征的

期望表示为

\[E[x] = \sum_x xP(X = x) \]

当函数是从分布\(P\)中抽取的随机变量时，\(f(x)\)的期望为

\[E_{x \sim P}[f(x)] = \sum_x f(x)P(x) \]

方差可以用来量化随机变量与期望的偏差

\[Var[X] = E[(X - E[X])^2] = E[X^2] - E[X]^2 \]

方差的平方根被称为标准差

本节主要补足了一些概率方面的内容