ExpRe[5] python[2] raise语句，条件断点

目录

• 从一道动规看raise的常见用法
  • 粗略编写算法
  • 出错
  • 用raise传递信息
  • raise的用法总结
• 条件断点
• 总结和问答练习

时效性
本篇撰写时间为2021.11.14，由于计算机技术日新月异，博客中所有内容都有时效和版本限制，具体做法不一定总行得通，链接可能改动失效，各种软件的用法可能有修改。但是其中透露的思想往往是值得学习的。
Windows 10家庭中文版，版本20H2，操作系统内部版本19042.1288
本篇前置：

• ExpRe[4] python[1] 单元测试，算法题对拍
  https://www.cnblogs.com/minor-second/p/15549364.html
• 大致知道python3中的异常，try机制

从一道动规看raise的常见用法

我们继续做算法设计与分析作业

考虑一个所有元素为正的\(n*n\)二维数组（邻接矩阵），已知其中有且仅有一条有向回路使得该回路上各权值乘积大于1，试找出该回路。（特别注意可以自己到自己连边，且这样的边也有可能权重大于1）

其实括号提示是我自己加的。有点坑。

粗略编写算法

我们粗略编写如下类似于Floyd算法的程序

def find_loop(n, mat):
    max_mat = []
    for i in range(n):
        max_mat.append(mat[i].copy())
        for j in range(n):
            max_mat[i][j] = [max_mat[i][j], -1]

    loop_start = 0

    try:
        for k in range(n):
            for i in range(n):
                for j in range(n):
                    if max_mat[i][k][0] * max_mat[k][j][0] > max_mat[i][j][0]:
                        max_mat[i][j][0] = max_mat[i][k][0] * max_mat[k][j][0]
                        max_mat[i][j][1] = k
                    if i==j and max_mat[i][j][0] > 1:
                        loop_start = i
                        raise StopIteration
    except StopIteration:
        seq = [loop_start, loop_start]

    def insert(i,max_mat,seq):
        s, e = seq[i], seq[i+1]
        if max_mat[s][e][1] == -1:
            return seq
        seq = seq[:i+1] + [max_mat[s][e][1]] + seq[i+1:]
        seq = insert(i+1,max_mat,seq)
        seq = insert(i,max_mat,seq)
        return seq

    return insert(0,max_mat,seq)

• 首先深度拷贝输入max_mat防止改变输入对象（以便于测试）。并把原先矩阵中单独的数改成两个元素的表，表的第0个分量为权重（或多个权重乘积），第1个分量为“插入的点”。
• 使用类似Floyd算法的三重循环结构，最外层是依次考察“插入这个点是否变好”。先考察“\(i\to j\)改成\(i\to 0\to j\)是否变好”等\(n^2\)个命题，再考察“\(i\to j\)改成\(i\to 1\to j\)是否变好”等\(n^2\)个命题。考察完至多全部\(k\)值共\(n^3\)个命题后就找到了回路。
  其中max_mat[i][j][1] = k语句就是存储插入的点，方便最后回溯得到路径。
• 为了得到路径，我们先得到一个路径上的点loop_start，然后递归地利用矩阵中记录的信息向其中插入中间节点。
  insert使用了递归，因此效率不会很高（当然都用python写算法题了也不在乎卡常了是吧）。
  insert函数有个细节是先插入i+1处，再插入i处，否则显然导致错误结果。

出错

我们编写一个单元测试看看该算法对不对。
文件树

在test2.py中，输入代码

import unittest
import random
from problem2 import find_loop
class Test(unittest.TestCase):
    def test_auto(self):
        for _ in range(100):
            mat = list(list(random.random() * 0.8 for i in range(10)) for i in range(10))
            l = [i for i in range(10)]
            random.shuffle(l)
            n = random.randrange(1, 11)
            l = l[:n]
            pair_list = list((l[i-1], l[i]) for i in range(len(l)))
            for pair in pair_list:
                MAGIC = 0.9999
                mat[pair[0]][pair[1]] = MAGIC
            last_pair = pair_list[-1]
            mat[last_pair[0]][last_pair[1]] *= MAGIC**(-len(l)-1)
            seq = find_loop(10, mat)
            self.assertIn(l[0], seq)
            seq = seq[:-1] * 2
            for i in range(len(seq)):
                if seq[i] == l[0]:
                    self.assertEqual(seq[i:i+len(l)],l)
                    break

if __name__ == '__main__':
    unittest.main()

• 其思路是先生成元素都在\(0\)至\(0.8\)的10阶方阵，然后随机生成一个不重复的整数序列l（使用了shuffle打乱）。
• 接着，例如对于序列[1, 2, 3]，生成二元组序列[(3,1), (1,2), (2,3)]（特别注意负数下标使用），并人工改变这些序列对应的邻接矩阵中的权值，造出一条权重乘积大于1的回路。
• 调用算法得到的seq未必和l相同。比如seq = [1,2,3,1]，l = [3,1,2]. 但我们只需把seq去掉末尾元再重复2遍，其中就一定包含l为“子串”了。

结果是有时能通过测试有时不能。试图改变循环次数100为更大或更小的数值，发现有一个概率量级为\(10^{-2} \sim 10^{-1}\)的错误。（回忆\((1-1/n)^n\approx 1/e\)）
报错RecursionError: maximum recursion depth exceeded in comparison.

用raise传递信息

我们用try包裹出错的seq = find_loop(10, mat)语句

            try:
                seq = find_loop(10, mat)
            except RecursionError:
                raise RecursionError(seq, l, mat)

多次运行，发现输出的共同特点是l == [0]. 这就方便找到错误了：当0到0路径权重大于1时，我们在0到0中间插入了点0，从而导致无限循环。（有趣的是，l == [1]不会发生此错误。因为此时在外层循环到k==1之前就已经能发现1到1的权重大于1了）

raise的用法总结

• 用法之一：可以看到我们使用try包裹代码段，并用raise手动引发异常，用except捕捉直接跳出多重循环。
• 用法之二：在异常后加括号，其中添加任意多个参数，从而传递信息。

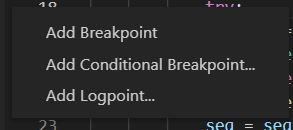
条件断点

对于新手（其实就是我），即使知道错误都出现在l == [0]，也未必能马上看出错误。此时可能需要打条件断点方便调试。

• 错误做法：

if 条件:
	pass

在pass处加断点可能无法起作用。因为pass语句作为占位符，可能不对应任何实际编译出的代码，直接被“忽略”。

• 一种比较丑陋的做法是把pass改成...（即所谓ellipsis）或0这种无作用的表达式，从而可加断点。
• 而比较好的做法是在VSCode中原本加断点的位置右键（如图），使用VSCode的条件断点功能。典型的是当满足某条件时中断。当然也有其它更强大的功能。
  
• 当然还可以使用高版本python的breakpoint()函数。

总结和问答练习

0. Q: 像本文中一样用异常跳出多重循环可能有什么坏处？
   A: 比如因为其他原因引起StopIteration时也被文中的except捕捉了。
   为了解决这个可以自定义异常类型。
1. Q: 从ExpRe[4]和[5]，你对“生成测试数据”有何感想？
   A: 随机生成数据可能由于概率原因无法覆盖一些情况。
   对于输入有限制的情况（比如本题），如果随机生成数据可能会丢弃（浪费）大量数据（甚至有时检测是否符合约束本身就很费劲）。
   如果人工生成符合约束的数据往往费时费力且分布“过于单一”难以考察各种情况。
   因此使用约束求解等方法生成测试数据确实是有用的技术。
2. Q: 解释文中错误发生的概率量级。
   A: 错误概率显然为\(1/100\)（l为单元素，且恰好为[0]，\(1/10*1/10 = 1/100\)），因此循环100次通过的概率大致为\(1/e\).
   实验证明，当单元测试中每次循环100次时，通过和不通过的情况大概在同一数量级。