线段树

线段树，一种非常通用的数据结构，多用于区间查询问题，虽然在时间和空间效率上都不如树状数组，但是因为其维护和操作更简单而受oier青睐

为了加深记忆 特此写篇博客 大佬轻喷

线段树，是一颗完全二叉树，由上到下维护，支持询问，更改等多种操作变种包括可持久化线段树及若干，本篇博客只提最简单的普通线段树，支持区间加法，乘法和询问

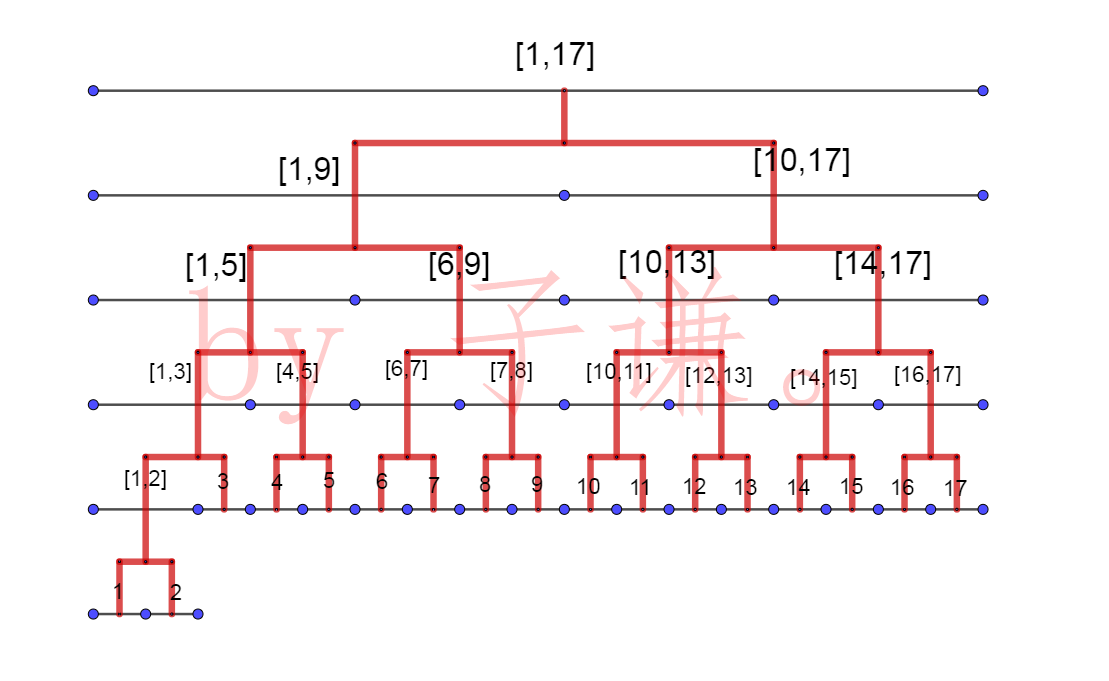
 线段树如图所示

由此可得代码

---

 

 

#include<bits/stdc++.h>

using namespace std;

const int N=4e5+5;

struct Segmentree{

    long long l,r,add,sum,mu;

    #define l(x) tree[x].l

    #define r(x) tree[x].r

    #define add(x) tree[x].add

    #define sum(x) tree[x].sum

    #define mu(x) tree[x].mu

}tree[N];

long long n,m,mod,a[N];

void build(int p,int l,int r)

{

    l(p)=l,r(p)=r,mu(p)=1;

    //此处mu初始化，乘法标记初始必须为1

    if(l==r){sum(p)=a[l]%mod;return;}

    long long mid=(l+r)>>1;

    build(p*2,l,mid);

    build(p*2+1,mid+1,r);

    sum(p)=(sum(p*2)+sum(p*2+1))%mod;

}//建树，没有差别，记得取模

void spread(int p)

{

    //sum数组处理

    //欲下传的乘法标记乘以下传处的总和    同时处理加法标记的问题 欲下传的加法标记乘以区间长度

    //左右区间分别处理

    sum(p*2)=(long long)(mu(p)*sum(p*2)+(r(p*2)-l(p*2)+1)*add(p)%mod)%mod;

    sum(p*2+1)=(long long)(mu(p)*sum(p*2+1)+((r(p*2+1)-l(p*2+1)+1)*add(p))%mod)%mod;

    //乘法标记处理

    //当前乘法标记乘以左（或右）儿子的乘法标记

    mu(p*2)=(long long)(mu(p*2)*mu(p))%mod;

    mu(p*2+1)=(long long)(mu(p*2+1)*mu(p))%mod;

    //加法标记处理

    //当前乘法标记乘以左（或右）儿子的乘法标记，再加上当前的加法标记

    add(p*2)=(long long)(mu(p)*add(p*2)+add(p))%mod;

    add(p*2+1)=(long long)(mu(p)*add(p*2+1)+add(p))%mod;

   

    mu(p)=1,add(p)=0;//处理完初始化

    //每步操作都要求取模

}

void changeadd(long long p,long long l,long long r,long long k)

{

    //对区间加法处理

    if(l(p)>=l&&r(p)<=r)

    {

        add(p)=(add(p)+k)%mod;

        sum(p)=(long long)(sum(p)+k*(r(p)-l(p)+1))%mod;

        return;

    }

    spread(p);//下传标记

    sum(p)=(sum(p*2)+sum(p*2+1))%mod;

    long long mid=(l(p)+r(p))>>1;

    if(l<=mid) changeadd(p*2,l,r,k);

    if(r>mid) changeadd(p*2+1,l,r,k);

    sum(p)=(sum(p*2)+sum(p*2+1))%mod;

   

}

void changemul(long long p,long long l,long long r,long long k)

{

    if(l(p)>=l&&r(p)<=r)

    {

        add(p)=(add(p)*k)%mod;

        //比较重要的一步,add要在这里乘上k,因为后面可能要加其他的数而那些数其实是不用乘k的

        //只需谨记 先乘再加

        mu(p)=(mu(p)*k)%mod;

        sum(p)=(sum(p)*k)%mod;

        return;

    }

    spread(p);//下传标记

    sum(p)=(sum(p*2)+sum(p*2+1))%mod;

    long long mid=(l(p)+r(p))>>1;

    if(l<=mid) changemul(p*2,l,r,k);

    if(r>mid) changemul(p*2+1,l,r,k);

    sum(p)=(sum(p*2)+sum(p*2+1))%mod;

}

long long ask(int p,int l,int r)

{

    //找到了

    //退出，返回初值

    if(l(p)>=l&r(p)<=r){

        return sum(p);

    }

    spread(p);//下传标记，调用下一层的值

    long long val=0;

    long long mid=(l(p)+r(p))>>1;

    if(l<=mid)val=(val+ask(p*2,l,r))%mod;

    if(mid<r)val=(val+ask(p*2+1,l,r))%mod;

    return val;

}

int main()

{

    cin>>n>>m>>mod;

    for(int i=1;i<=n;i++)

        cin>>a[i];

    build(1,1,n);//建树入口

    for(int i=1;i<=m;i++)

    {

        int x;

        cin>>x;

        if(x==1)

        {

            long long a,b,c;

            cin>>a>>b>>c;

            changemul(1,a,b,c);

        }

        else if(x==2)

        {

            long long a,b,c;

            cin>>a>>b>>c;

            changeadd(1,a,b,c);

        }

        else{

            long long a,b;

            cin>>a>>b;

            printf("%lld\n",ask(1,a,b));

        }

    }

    return 0;

}

 

---