【论文考古】量化SGD Deep Learning with Limited Numerical Precision

S. Gupta, A. Agrawal, K. Gopalakrishnan, and P. Narayanan, “Deep Learning with Limited Numerical Precision,” arXiv:1502.02551 [cs, stat], Feb. 2015, Accessed: Mar. 07, 2022. [Online]. Available: http://arxiv.org/abs/1502.02551

简介

为了缓解训练深度神经网络时计算资源的限制，文章考虑用有限精度的数据（也就是低精度定点数而非浮点数）来进行训练。文章发现用16比特宽的定点数表示以及随机取整时，在图片分类上与浮点数没有明显的性能差异。与之前的文章相比，特色在于：1）文章并非只考虑前向传播时的量化，而是在整个训练过程中都考虑量化；2）考虑DNN、CNN等深度网络；3）考虑随机取整。

观点

• 神经网络训练过程中的噪声对于性能提升是有益的，其error resiliency在2010年左右得到了较多研究

  计算不一定需要高精度，甚至可以是approximate、non-deterministic

• 定点数相较于浮点数有两方面优势：

  • 计算速度更快、硬件资源消耗更少
  • 占用内存更少，可以计算更大的模型

• 采用无偏的随机取整是十分重要的，否则必须要用32定点数表述才能进行MNIST的CNN训练。

  \[\text { Round }(x,\langle\text { IL }, \text { FL }\rangle)= \begin{cases}\lfloor x\rfloor & \text { w.p. } 1-\frac{x-\lfloor x\rfloor}{\epsilon} \\ \lfloor x\rfloor+\epsilon & \text { w.p. } \frac{x-\lfloor x\rfloor}{\epsilon}\end{cases} \]

实验

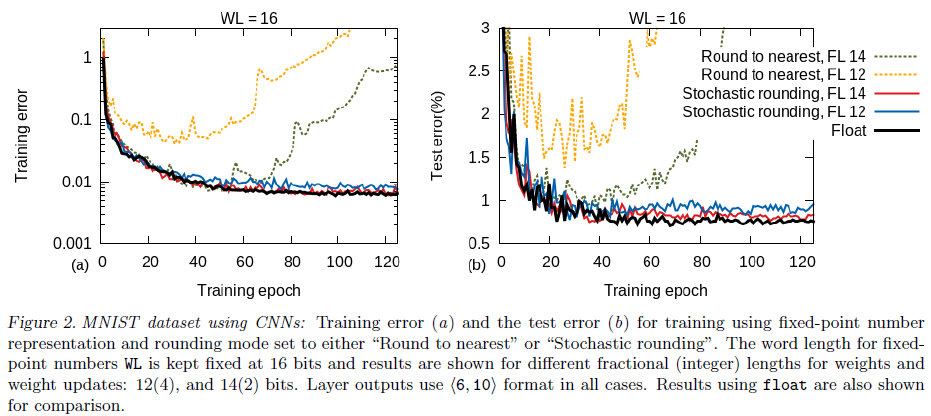
• CNN比DNN更容易收到量化的影响，低精度下会直接无法收敛

  

• 量化在训练前期的影响不大，主要在训练后期。因为这是梯度是稀疏且接近零的，如果采用固定量化会直接取零，精度不够也会导致无法继续更新

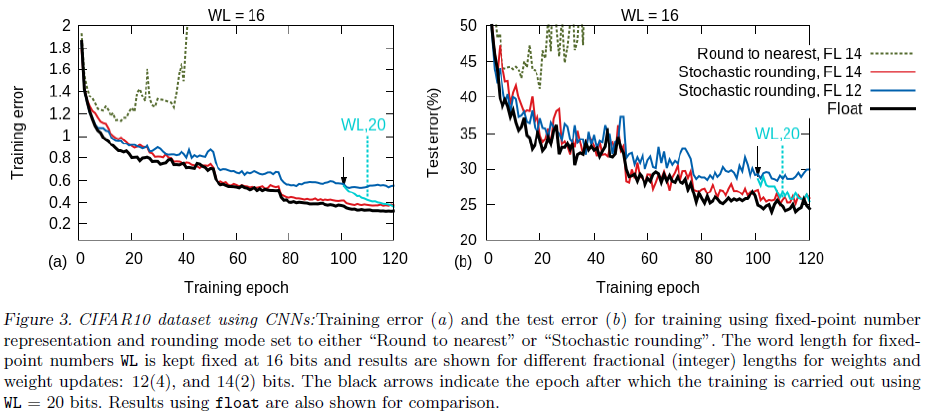
• 量化造成的性能损耗是可逆的。如果在后期增大量化的位数，只需要增加15-20个epoch就可以训练到浮点数的性能。因此一个训练策略是先使用低精度定点计算和随机取整，在学习进入平台期后微调量化精度，这就是混合精度计算。

  

借鉴

• 文章结合硬件的co-optimized system与结合信道的思路是一致的
• 如果在写问扎根的时候看到了一个相似度非常高的work，新增一些独特的工作（比如硬件的设计）来找补回来。