题解：P2611 [ZJOI2012] 小蓝的好友

思路

算至少有一个点的矩形可以转化成所有矩形减去没有任何点的矩形。

接下来问题转化成算没有任何点的矩形。

考虑扫描线，我们从上往下扫，每个矩形的下边界一定贴着扫描线。

我们接下来所说的坐标为从左到右第 \(x\) 行，从上到下第 \(y\) 列。

设 \(p_i\) 为第 \(i\) 列离扫描线最近的点的横坐标（一定是扫过的点）。

如图，蓝色点是 \(p_i\) 的位置， 红色点是扫描线。

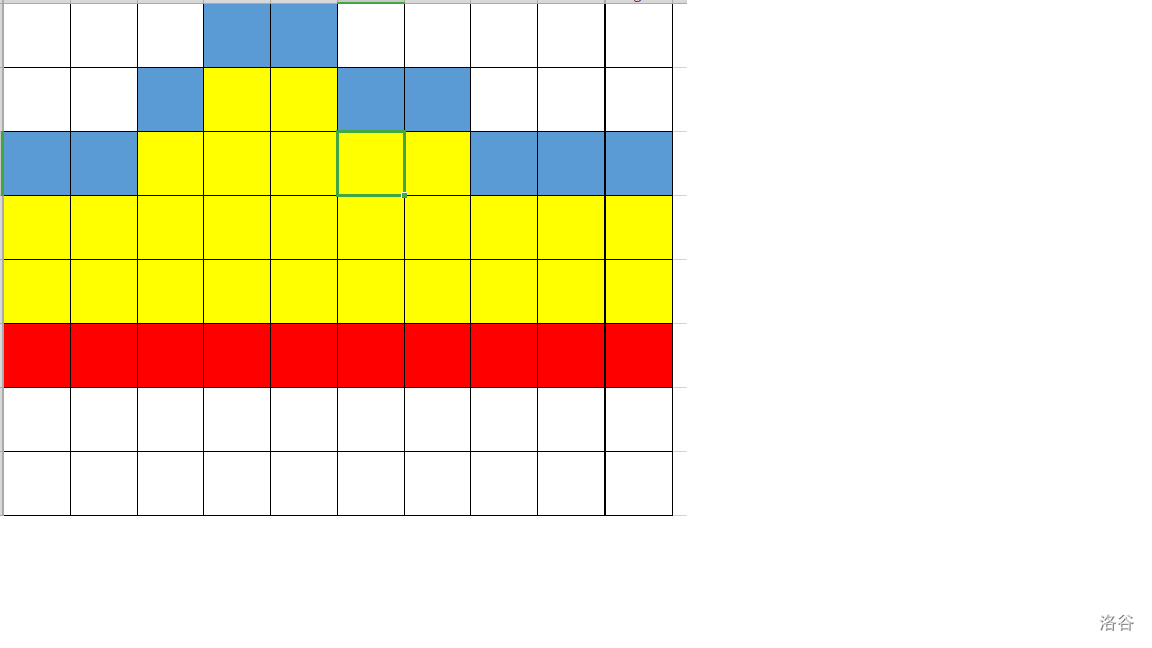
如何不重不漏的数出所有长方形？

这让我想起了一道笛卡尔树经典题 Largest Rectangle in a Histogram，不过用单调栈也能做。

我们对点 \((i，p_i)\) 建笛卡尔树，\(i\) 为键值，\(p_i\) 为堆值，大根堆。

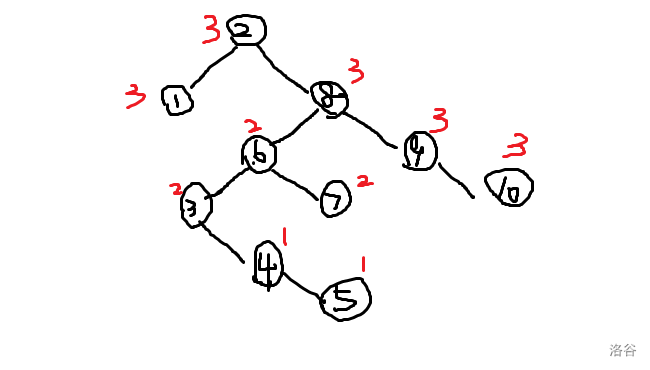
如何用这棵笛卡尔算出所有长方形？

设 \(h\) 为扫描线，纵坐标先抛出结论：

\[Ans = \Sigma _ i {(h - p_i)\times(size_{ls}+1) \times (size_{rs} + 1)} \]

对着图看应该就懂了。

这个笛卡尔树可以用 FHQ Treap 维护，Treap 本来就是笛卡尔树的一种，由于坐标随机所以树高期望为 \(\log(n)\)

细节

初始建一个全为零的笛卡尔树。

从上往下扫，先修改再查询。

维护两个值 \(sum1 = \Sigma_i{ (size_{ls}+1) \times (size_{rs} + 1)},sum2 = \Sigma_i{ p_i \times (size_{ls}+1) \times (size_{rs} + 1)}\)

\(Ans = sum1 \times h -sum2\)

剩下的看代码吧

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 1e5 + 10;
int r, c, n;
int ch[maxn][2], pri[maxn], sze[maxn], val[maxn], rt, cnt;
int sum1[maxn], sum2[maxn];
vector<int> v[maxn];
int newnode(int x, int y) {
	cnt++;
	val[cnt] = x, pri[cnt] = y;
	sze[cnt] = 1;
	return cnt;
}
void update(int x) {
	int res = (sze[ch[x][0]] + 1) * (sze[ch[x][1]] + 1);
	sum1[x] = sum1[ch[x][0]] + sum1[ch[x][1]] + res;
	sum2[x] = pri[x] * res + sum2[ch[x][0]] + sum2[ch[x][1]];
	sze[x] = sze[ch[x][0]] + sze[ch[x][1]] + 1;
}
int merge(int x, int y) {
	if(x == 0 || y == 0) return x + y;
	if(pri[x] > pri[y]) {
		ch[x][1] = merge(ch[x][1], y);
		update(x);
		return x;
	} 
	else {
		ch[y][0] = merge(x, ch[y][0]);
		update(y);
		return y;
	} 
}

void split(int u, int k, int &L, int &R) {
	if(!u) {
		L = R = 0;
		return;
	}
	if(sze[ch[u][0]] + 1 <= k) {
		L = u;
		split(ch[u][1], k - sze[ch[u][0]] - 1, ch[u][1], R);
	}
	else {
		R = u;
		split(ch[u][0], k, L, ch[u][0]);
	}
	update(u);
}

void print(int x) {
	if(!x) return;
	print(ch[x][0]);
	print(ch[x][1]);
}
signed main() {
	cin >> r >> c >> n;
	for(int i = 1; i <= n; i++) {
		int x, y; cin >> x >> y;
		v[x].push_back(y);
	}
	for(int i = 0; i <= c; i++) {
		rt = merge(rt, newnode(i, 0));
	}
	int ans = 0;
	for(int i = 1; i <= r; i++) {
		for(auto t : v[i]) {
			int L = 0, R = 0, p = 0;
			split(rt, t + 1, L, R);
			split(L, t, L, p);
			pri[p] = i;
			rt = merge(merge(L, p), R);
		}
		int L = 0, p = 0;
		split(rt, 1, L, p);
		ans += sum1[p] * i;
		ans -= sum2[p];
		rt = merge(L, p);
	}
	ans = (r * (r + 1)) * (c * (c + 1)) / 4 - ans;	
	cout << ans;
	return 0;
}