§1. 拉格朗日定理和函数的单调性

掌握罗尔定理，拉格朗日定理，达布定理及其推论，会运用导数判断函数的（严格）增减性。

重点习题：第2、5、6、7题。

 

 

 

米歇尔·罗尔（Michel Rolle，1652年4月21日－1719年11月8日），是法国数学家。他著名的有罗尔定理（1691年）。他也发明了现在的标准记法以表示x的n次根。

 

他出生于小店家庭，只受过初等教育，且过早结婚，年轻时贫困潦倒，靠充当公证人与律师抄录员的微薄收入养家糊口，他利用业余时间刻苦自学代数与丢番图的著作，并很有心得。 1682年，他解决了数学家奥扎南提出一个数论难题，受到了学术界的好评，从而名声鹊起，也使他的生活有了转机，此后担任初等数学教师和陆军部行征官员。1685年进入法国科学院，担任低级职务，到1690年才获得科学院发给的固定薪水。此后他一直在科学院供职，1719年因中风去世。

 

罗尔所处的时代正当牛顿、莱布尼兹的微积分诞生不久，由于这一新生事物存在逻辑上的缺陷，从而遭受多方面的非议，其中也包括罗尔，并且他是反对派中最直言不讳的一员。1700年，在法国科学院发生了一场有关无穷小方法是否真实的论战。在这场论战中，罗尔认为无穷小方法由于缺乏理论基础将导致谬误，并说：“微积分是巧妙的谬论的汇集”。瓦里格农、索弗尔等人之间，展开了异常激烈的争论。约翰。贝努利还讽刺罗尔不懂微积分。由于罗尔对此问题表现得异常激动，致使科学院不得不屡次出面干预。直到1706年秋天，罗尔才向瓦里格农、索弗尔等人承认他已经放弃了自己的观点，并且充分认识到无穷小分析新方法价值。

 

罗尔在数学上的成就主要是在代数方面，专长于丢番图方程的研究。 罗尔于1691年在题为《任意次方程的一个解法的证明》的论文中指出了：在多项式方程f(x)=0的两个相邻的实根之间，方程f'(x)=0至少有一个根。在一百多年后，1846年尤斯托（Giusto Bellavitis）将这一定理推广到可微函数，尤斯托还把此定理命名为罗尔定理。罗尔定理的诞生是十分有趣的，他只是做了一个小小的假设，而且并没有证明，但现在，他的定理却出现在每一本微积分教材上。

 

罗尔还研究并得到了与现在相一致的实数集的序的概念。他促成了目前所采用的负数大小顺序性的建立，而在他之前，笛卡儿及同时代的许多人都认为-2<-5，罗尔自1691年就已采用了现在的负数的大小排列顺序。他明确说：“我认为-2a是一比-5a大的量。”（其中a是一个正实数）罗尔在《代数学讲义》一书中设计了一个数a的n次方根的符号为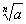（而在他之前，则是用符号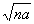来表示a的n次方根），他的这个符号立刻被普遍地接受，并沿用直今。

 

 

 

 

拉格朗日中值定理又称拉氏定理，是微分学中的基本定理之一，它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。拉格朗日中值定理是罗尔中值定理的推广，同时也是柯西中值定理的特殊情形，是泰勒公式的弱形式（一阶展开）。

 

法国数学家拉格朗日于1797年在其著作《解析函数论》的第六章提出了该定理，并进行了初步证明，因此人们将该定理命名为拉格朗日中值定理。

 

约瑟夫·拉格朗日（Joseph-Louis Lagrange，1736~1813）全名为约瑟夫·路易斯·拉格朗日，法国著名数学家、物理学家。1736年1月25日生于意大利都灵，1813年4月10日卒于巴黎。他在数学、力学和天文学三个学科领域中都有历史性的贡献，其中尤以数学方面的成就最为突出。拉格朗日是18世纪的伟大科学家，在数学、力学和天文学三个学科中都有历史性的重大贡献。但他主要是数学家，拿破仑曾称赞他是“一座高耸在数学界的金字塔”，他最突出的贡献是在把数学分析的基础脱离几何与力学方面起了决定性的作用。使数学的独立性更为清楚，而不仅是其他学科的工具。同时在使天文学力学化、力学分析化上也起了历史性作用，促使力学和天文学（天体力学）更深入发展。由于历史的局限，严密性不够妨碍着他取得更多的成果。

 

拉格朗日父姓拉格朗日亚（Lagrangia）。拉格朗日在都灵出生受洗记录上的正式名字为约瑟普·洛德维科·拉格朗日亚（Giuseppe Lodovico，Lagrangia）。父名弗朗切斯科·洛德维科·拉格朗日亚（Francesco Lodovico， Lagrangia）；母名泰雷萨·格罗索（Teresa Grosso）。他曾用过的姓有德·拉·格朗日（De la Grange），拉·格朗日（La Grange）等。去世后，法兰西研究院给他写的颂词中，正式用约瑟夫·拉格朗日（Joseph-Louis Lagrange ）。父系为法国后裔。曾祖是法国骑兵上校，到意大利后与罗马家族的人结婚定居；祖父任都灵的公共事务和防务局会计，又同当地人结婚。父亲也在都灵同一单位工作，共有11个子女，但大多数夭折，拉格朗日最大。

 

到了青年时代，在数学家雷维里的教导下，拉格朗日喜爱上了几何学。17岁时，他读了英国天文学家哈雷的介绍牛顿微积分成就的短文《论分析方法的优点》后，感觉到“分析才是自己最热爱的学科”，从此他迷上了数学分析，开始专攻当时迅速发展的数学分析。

 

18岁时，拉格朗日用意大利语写了第一篇论文，是用牛顿二项式定理处理两函数乘积的高阶微商，他又将论文用拉丁语写出寄给了当时在柏林科学院任职的数学家欧拉。不久后，他获知这一成果早在半个世纪前就被莱布尼兹取得了。这个并不幸运的开端并未使拉格朗日灰心，相反，更坚定了他投身数学分析领域的信心。

 

1755年拉格朗日19岁时，在探讨数学难题“等周问题”的过程中，他以欧拉的思路和结果为依据，用纯分析的方法求变分极值。第一篇论文“极大和极小的方法研究”，发展了欧拉所开创的变分法，为变分法奠定了理论基础。变分法的创立，使拉格朗日在都灵声名大振，并使他在19岁时就当上了都灵皇家炮兵学校的教授，成为当时欧洲公认的第一流数学家。1756年，受欧拉的举荐，拉格朗日被任命为普鲁士科学院通讯院士。

 

1764年，法国科学院悬赏征文，要求用万有引力解释月球天平动问题，他的研究获奖。接着又成功地运用微分方程理论和近似解法研究了科学院提出的一个复杂的六体问题（木星的四个卫星的运动问题），为此又一次于1766年获奖。

 

1766年德国的腓特烈大帝向拉格朗日发出邀请时说，在“欧洲最大的王”的宫廷中应有“欧洲最大的数学家”。于是他应邀前往柏林，任普鲁士科学院数学部主任，居住达20年之久，开始了他一生科学研究的鼎盛时期。在此期间，他完成了《分析力学》一书，这是牛顿之后的一部重要的经典力学著作。书中运用变分原理和分析的方法，建立起完整和谐的力学体系，使力学分析化了。他在序言中宣称：力学已经成为分析的一个分支。

 

1783年，拉格朗日的故乡建立了"都灵科学院"，他被任命为名誉院长。1786年腓特烈大帝去世以后，他接受了法王路易十六的邀请，离开柏林，定居巴黎，直至去世。

 

这期间他参加了巴黎科学院成立的研究法国度量衡统一问题的委员会，并出任法国米制委员会主任。1799年，法国完成统一度量衡工作，制定了被世界公认的长度、面积、体积、质量的单位，拉格朗日为此做出了巨大的努力。

 

1791年，拉格朗日被选为英国皇家学会会员，又先后在巴黎高等师范学院和巴黎综合工科学校任数学教授。1795年建立了法国最高学术机构——法兰西研究院后，拉格朗日被选为科学院数理委员会主席。此后，他才重新进行研究工作，编写了一批重要著作：《论任意阶数值方程的解法》、《解析函数论》和《函数计算讲义》，总结了那一时期的特别是他自己的一系列研究工作。

 

1813年4月3日，拿破仑授予他帝国大十字勋章，但此时的拉格朗日已卧床不起，4月11日早晨，拉格朗日逝世。

 

 

 

让·加斯东·达布（Jean Gaston Darboux，1842年8月14日－1917年2月23日）法国数学家。他对数学分析(积分，偏微分方程)和微分几何(曲线和曲面的研究)作出了重要贡献。他于1876年获得科学院大奖，于1884年成为其成员。他在子午线局的继任是Paul Appell。他是1916年皇家学会Sylvester勋章的获得者。

达布是法国数学家。1842年8月14日生于尼姆；1917年2月23日卒于巴黎。

达布幼年丧父，家境清贫，但他勤奋好学，上完中学后，1861年以名列榜首的骄人成绩考入巴黎高等师范学校学习，大学四年级时就脱颖而出，发表了一篇关于正交曲面的论文，1864年大学毕业后留校任教并攻读博士学位，1866年7月获博士学位，以后相继在两所中学及法兰西学院、巴黎大学、索邦大学、巴黎师范学校任教，1880年起成为巴黎师范学校的教授。1889-1903年任巴黎大学理学院院长，后任名誉院长。他于1876年获得科学院大奖，1884年当选为法国科学院院士。1895年被选为彼得堡科学院通讯院士。同时还被聘为英国皇家学会会员和其他国家科学会的会员，并荣获国内外许多大学的名誉学位。

达布在数学和物理的许多方面都很有建树，特别是在数学分析、微分几何、微分方程等领域有更大的贡献。

在数学分析方面，他对函数连续性作了深入的研究。给出了一个“病态函数”，当从x=a变到x=b时，这个函数取遍两个给定值之间的一切中间值，但它却不是连续的函数。

达布对黎曼积分理论作了推广。他严格地证明了，不连续函数也可以求定积分，而且间断点可以有无穷多个，只要它们包含在长度可以任意小的有限个区间之内就行。即证明了一个有界函数f(x)在[a,b]上可积的充要条件是f(x)的间断点组成一个测度为零的集合。他在1875年还给出了推广意义上的微积分基本定理的证明。现在定积分理论里的所谓上积分、下积分、达布大和、达布小和以及达布定理等都是以他的姓氏命名的。

在解析函数论方面，他研究了球函数、正交函数，包括雅可比多项式的分解等问题，并取得了重要成果。

在微分几何方面，他关于曲面理论和曲线坐标的研究获得了许多重要结果，他研究了测地线及曲面的变形，并创立了流动坐标系方法。他的《曲面的一般理论和微积分的几何应用教程》(4卷，1887-1896年)是一部名著，在这部书中，不仅系统地介绍了18-19世纪曲线和曲面几何学方面所取得的成就，而且还包含了他自己研究的许多成果，此外，在这部著作中还可以看到射影几何的思想。

在微分方程方面，他研究了一阶常微分方程等问题。关于常微分方程的奇异解理论就是达布于1872年完成的。一般偏微分方程通解的定义，也是达布给出的。他还研究了微分方程的可积性及积分法问题，总结了拉普拉斯的级联方法，并将其应用于所有二阶偏微分方程中。他对用于非线性方程的蒙日方法作了较精确的阐述，被称为达布方程。

在物理学方面，他研究过运动学、平衡、点系微振等问题，并取得了成果。达布成功地解决了运动学、平衡、点系微振等各种问题。许多物理上的概念如矢量、张量、线、面、束等，都是与他的名字分不开的。

在数学中以他的姓氏命名的有：达布和、达布曲线、达布曲面、达布向量、达布张量、达布束、达布标架、达布不变量、达布常微分方程、达布问题、达布性质、达布方向、达布方程，等等。而以他的姓氏命名的定理有多个。

达布1870年创办了有名的数学杂志《数学科学通报》。

他的著作还有：《二阶偏微分方程》(1870年)、《论异常曲线和代数曲面类及虚数理论》(1873年)、《论间断函数》(1875年)、《正交系和曲线坐标教程》(1898年)等。