§1. 实数

§1. 实数

1.如何用一个无限小数表示一个实数。

2.n位不足近似和n位过剩近似的定义和应用（P2，命题）。

3.利用P3例2，比较两个数的大小。

4绝对值的定义和性质（性质3和性质4最重要）。

重点习题：习题3

 

第一次数学危机

古希腊的毕达哥拉斯学派信奉“数即万物”，并认为宇宙间各种关系都可以用整数或整数之比来表达。属于毕达哥拉斯学派的希帕索斯（Hippasus）发现边长为1的正方形的对角线长度不能用整数或分数来表达。于是毕达哥拉斯学派对这个新发现的“怪数”保密，可希帕索斯则无意中泄露了这个发现，于是被毕达哥拉斯学派的人扔进大海淹死了（希帕索斯被淹死是多个传说中一个，另还有被众神（毕达哥拉斯学派信仰的数字之神）判处淹死，开除学派等说法）。无理数的发现，极大地推动了数学的发展。

无理数

无理数是指除有理数以外的实数，当中的“理”字来自于拉丁语的rationalis，意思是“理解”，实际是拉丁文对于logos“说明”的翻译，是指无法用两个整数的比来说明一个无理数。

非有理数之实数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环，即无限不循环小数。常见的无理数有大部分的平方根、π和e（其中后两者同时为超越数）等。无理数的另一特征是无限的连分数表达式。

性质: 1. 无理数加或减有理数必得无理数。  2. 无理数乘不等于0的有理数必得无理数。

不知是否是无理数的数: π +e,π − e等，事实上，对于任何非零整数m及n，不知道 mπ +ne 是否无理数。无理数与无理数的四则运算的结果往往不知道是否无理数，只有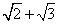等除外。我们亦不知道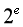,,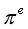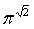是否无理数。

 

阿基米德  

阿基米德（公元前287年—公元前212年），伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家，静态力学和流体静力学的奠基人，并且享有“力学之父”的美称，阿基米德和高斯、牛顿并列为世界三大数学家。

公元前287年，阿基米德出生在古希腊西西里岛东南端的锡拉库扎城。阿基米德的父亲是天文学家和数学家，所以他从小受家庭影响，十分喜爱数学。大概在他九岁时，父亲送他到埃及的亚历山大城念书，亚历山大城是当时西方世界的知识、文化中心，学者云集，举凡文学、数学、天文学、医学的研究都很发达，阿基米德在这里随许多著名的数学家学习，包括有名的几何学大师欧几里得，因此奠定了他日后从事科学研究的基础。

在经过许多年的求学历程后，阿基米德回到故乡锡拉库扎。据说锡拉库扎的国王希伦二世与阿基米德的父亲是朋友，也有另一种说法：国王与他们是亲戚关系。总之，回国后的阿基米德受到国王的礼遇，经常出入宫廷，并常与国王、大臣们畅谈国事或闲话家常。阿基米德在这种优裕的环境下，作了几十年的研究工作，并在数学、力学、机械方面取得了许多重要的发现与成就，成为上古时代欧洲最有创建的科学家。

据说阿基米德经常为了研究而废寝忘食，走进他的住处，随处可见数字和方程式，地上则是画满了各式各样的图形，墙上与桌上也无法幸免地成了他的计算板，由此可见他精力的旺盛。

真假皇冠

国王请金匠用纯金打造了一顶纯金王冠，做好了以后，国王怀疑金匠不老实，可能造假掺了“银”在里面，但是又不能把王冠毁坏来鉴定。怎样才能检验王冠是不是纯金的呢？阿基米德想了好久，一直没有好方法，吃不下饭也睡不好觉。 有一天，他在洗澡的时候发现，当他坐在浴盆里时水位上升了，这使得他想到了：“上升了的水位正好应该等于王冠的体积，所以只要拿与王冠等重量的金子，放到水里，测出它的体积，看看它的体积是否与王冠的体积相同，如果王冠体积更大，这就表示其中造了假，掺了银。”

阿基米德想到这里，不禁高兴的从浴盆跳了出来，裸露身体就跑了出去，边跑还边喊著“εύρηκα！（我发现了！）”果然经过证明之后，王冠中确实含有其他杂质，阿基米德成功的揭穿了金匠的诡计，国王对他当然是更加的信服了。

后来阿基米德将这个发现进一步总结出浮力理论，为浮体学建立了基本的定理，并写在他的《浮体论》著作里，也就是：物体在浮体中所受的浮力，等于物体所排开的浮体的重量。

举起地球

阿基米德说过：“给我一个支点，我可以举起整个地球。”

阿基米德对于机械的研究源自于他在亚历山大城求学时期。有一天阿基米德在久旱的尼罗河边散步，看到农民提水浇地相当费力，经过思考之后他发明了一种利用螺旋作用在水管里旋转而把水吸上来的工具，后世的人叫它做“阿基米德螺旋提水器”，埃及一直到二千年后的现在，还有人使用这种器械。这个工具成了后来螺旋推进器的先祖。

当时的欧洲，在工程和日常生活中，经常使用一些简单机械，譬如螺丝、滑车、杠杆、齿轮等，阿基米德花了许多时间去研究，发现了“杠杆原理”和“力矩”的观念，对于经常使用工具制作机械的阿基米德而言，将理论运用到实际的生活上是轻而易举的。他曾说只要给他一个支点，他就可以举起整个地球（当然这只是比喻，因为太空没有重力）。

刚好此时国王希伦二世遇到了一个棘手的问题：他替埃及托勒密王造了一艘船，但因为船太大太重，无法放进海里，国王就对阿基米德说：“你连地球都举得起来，把一艘船放进海里应该很容易吧？”于是阿基米德迅速地巧妙组合各种机械，造出一架机具。在一切准备妥当后，将牵引机的绳子交给国王，国王轻轻一拉，大船果然移动下水，国王不得不为阿基米德的天才所慑服。从这个历史故事我们可以知道，阿基米德可能是当时全世界对于机械的原理与运用，了解最透彻的人。

公元前3世纪末正是罗马共和国与北非迦太基帝国，为了争夺西西里岛的霸权而开战的时期。地处西西里岛的锡拉库扎一直都是投靠罗马，但是公元前216年迦太基大败罗马军队，锡拉库扎的新国王（希伦二世的孙子继任），立即见风转舵与迦太基结盟，罗马共和国于是派马克卢斯将军领军从海路和陆路同时进攻锡拉库扎。国难当前，保家卫国的责任感促使阿基米德奋起抗敌，于是他绞尽脑汁，日以继夜的发明各种御敌武器。

根据一些年代较晚的记载，当时他造了巨大的起重机，可以将敌人的战舰吊到半空中，然后重重摔下使战舰在水面上粉碎；他还利用杠杆原理制造出一批投石机，凡是靠近城墙的敌人，都难逃他飞石与标枪的攻击。这些武器弄得罗马军队惊慌失措、人人害怕，连大将军马克卢斯也不得不承认“这是场罗马舰队与阿基米德一人的战争”、“阿基米德简直是神话中的百手巨人”。

有一天叙拉古城遭到了罗马军队的偷袭，而叙拉古城的青壮年和士兵们都上前线去了，城里只剩下了老人、妇女和孩子，处于万分危急的时刻。就在这时，阿基米德为了自己的祖国站了出来。

阿基米德让妇女和孩子们每人都拿出自己家中的镜子一齐来到海岸边，让镜子把强烈的阳光反射到敌舰的主帆上，千百面镜子的反光聚集在船帆的一点上，船帆燃烧起来了，火势趁着风力，越烧越旺，罗马人不知底细，以为阿基米德又发明了新武器。就慌慌张张地逃跑了。

由于久攻不下，马克卢斯决定改变策略，以围城的持久战来断绝城内粮食，这个妙计使得阿基米德也无可奈何。公元前212年，锡拉库扎城终于被罗马军队攻陷。相传罗马军队进城时，阿基米德还在自家前的地上画图研究几何问题，一个罗马战士走近沉思中的阿基米德，要求他立刻前去面见马克卢斯，并踩坏了沙地上画的图形。阿基米德大吼：“走开，别踩坏我的图形！我要解开这个问题。”战士被激怒了，完全不管长官发出的保护令，拔出剑砍向阿基米德，这位伟大的科学家就这么一命呜呼了。

马克卢斯听到这消息后十分悲痛，马塞拉斯将杀死阿基米德的士兵当作杀人犯予以处决，为阿基米德建了一座刻有球内切圆柱图形的墓，来表达他对这位伟大科学家及伟大对手的敬意。

数学大师

阿基米德在数学上也有着极为光辉灿烂的成就，特别是在几何学方面。

阿基米德的数学思想中蕴涵微积分，阿基米德的《方法论》中已经“十分接近现代微积分”，这里有对数学上“无穷”的超前研究，贯穿全篇的则是如何将数学模型进行物理上的应用。

阿基米德将欧几里德提出的趋近观念作了有效的运用。他利用“逼近法”算出球面积、球体积、抛物线、椭圆面积，后世的数学家依据这样的“逼近法”加以发展成近代的“微积分”。阿基米德还利用割圆法求得π的值介于3.14163和3.14286之间。

另外他算出球的表面积是其内接最大圆面积的四倍，又导出圆柱内切球体的体积是圆柱体积的三分之二，这个定理就刻在他的墓碑上。

阿基米德研究出螺旋形曲线的性质，现今的“阿基米德螺线”曲线，就是因为纪念他而命名。另外他在《数沙者》一书中，他创造了一套记大数的方法，简化了记数的方式。