第3节 非负可测函数的勒贝格积分

学习目标:掌握非负可测函数勒贝格积分的定义与性质,特别是莱维定理和法图引理.

重点内容:

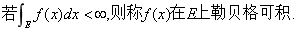
Levi定理

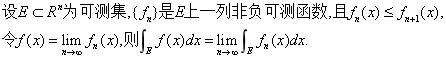
逐项积分定理

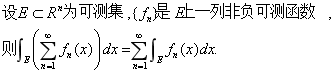
法图引理

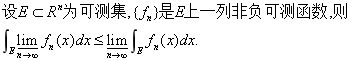
注意此处不是相等!

 

这是来自deepseek的人物介绍

贝波·列维（Beppo Levi，1875年8月14日－1961年8月28日）是意大利著名的数学家，以其在数学分析、集合论和代数几何等领域的工作而闻名。

以下是对他的中文介绍：

 

生平与教育

 

贝波·列维出生于意大利的都灵，早年在家乡接受教育，后在都灵大学学习数学，师从著名数学家科拉多·塞格雷（Corrado Segre）和朱塞佩·皮亚诺（Giuseppe Peano）。他于1896年获得博士学位，并迅速在数学界崭露头角。

 

学术贡献

 

数学分析：列维在实分析和复分析领域做出了重要贡献，尤其是在函数论和积分理论方面。他研究了可测函数和积分的性质，为后来的勒贝格积分理论奠定了基础。

 

集合论：他在集合论中提出了“列维引理”（Baire–Levi lemma），这是关于完备度量空间中闭集性质的重要结果。此外，他还研究了序数和超限数的理论。

 

代数几何：列维对代数几何也有深入研究，特别是在代数曲面的分类和性质方面。他的工作为现代代数几何的发展提供了重要工具。

 

数学基础：作为皮亚诺的学生，列维对数学基础问题（如公理系统和逻辑）也有浓厚兴趣，并在这方面发表了一些重要论文。

 

教职与影响

 

列维曾在多所意大利大学任教，包括博洛尼亚大学和比萨大学。1928年，由于政治原因（反对法西斯政权），他移居阿根廷，并在罗萨里奥大学和布宜诺斯艾利斯大学继续教学和研究工作。他在阿根廷培养了许多优秀的数学家，对南美的数学发展产生了深远影响。

 

个人生活与荣誉

 

列维一生致力于数学研究和教育，晚年仍活跃在学术领域。1961年，他在阿根廷的布宜诺斯艾利斯去世。为纪念他的贡献，意大利和阿根廷的多个学术机构设立了以他命名的奖项和讲座。

 

总结

 

贝波·列维是20世纪上半叶最重要的数学家之一，他的工作在多个领域具有深远影响。尽管因政治原因离开意大利，但他始终保持着对数学的热情，并为数学的国际化传播作出了重要贡献。

 

皮埃尔·约瑟夫·路易·法图（Pierre Joseph Louis Fatou，1878年2月28日－1929年8月10日）是法国数学家，主要贡献在复分析、动力系统和测度论等领域。

以下是他的个人简介：

早年生活与教育

出生于法国洛里昂（Lorient），自幼展现出数学天赋。1898年进入巴黎高等师范学院（École Normale Supérieure）学习，师从著名数学家如埃米尔·博雷尔（Émile Borel）和亨利·勒贝格（Henri Lebesgue）。1906年获得博士学位，论文题目为《关于三角级数和解析函数》（Sur les séries trigonométriques et les séries de Taylor）。

主要学术贡献

法图引理（Fatou's Lemma）

在实分析和测度论中，法图引理是关于勒贝格积分极限的重要结果。这一引理成为现代分析学（如概率论、泛函分析）的基础工具之一。

复分析与法图集（Fatou Set）

研究复动力系统时，他提出了法图集的概念，即在迭代函数下表现稳定的点的集合。与之相对的是朱利亚集（Julia Set），两者共同构成复动力系统的核心理论。法图的工作为后来曼德博集合（Mandelbrot Set）的研究奠定了基础。

函数论与泰勒级数

博士论文研究了泰勒级数的收敛性，并给出了法图定理（Fatou's Theorem），涉及解析函数的边界行为。

职业生涯

长期在巴黎天文台工作，担任天文学家，但仍专注于数学研究。与加斯顿·朱利亚（Gaston Julia）、皮埃尔·蒙特尔（Paul Montel）等数学家合作，推动复动力系统的发展。因性格低调，部分成果（如法图引理）最初未被广泛关注，后经勒贝格等人推广才成为经典。

晚年与荣誉

1929年因长期健康问题在法国佩萨克（Pessac）去世，年仅51岁。尽管生前名声不显，但他的工作对20世纪数学影响深远，尤其是动力系统领域。月球上的“法图环形山”以他命名，以纪念其贡献。