第2节 集合的运算

掌握集合的交, 并, 补, 差, 上下极限, 极限. 运用运算的性质和德摩根公式证明集合相等.

难点: 求集合列的上下极限.

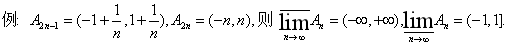
注: 求集合列的上下极限的主要方法是利用定理3.

 

 

 

德·摩根　Augustus De Morgan (1806～1871)

 

19世纪英国数学家、逻辑学家。生于印度，出生后刚 7个月就回到英国。卒于伦敦。他在少年时代就对数学发生浓厚的兴趣，1823年考入剑桥大学三一学院，1827年毕业。1828年后在伦敦的大学学院任数学教授多年。他曾任伦敦数学学会第一届会长。

 

德·摩根对19世纪数学的发展作出了贡献。他于1838年提出以“数学归纳法”的概念描述以往数学家们曾经使用的证明定理的方法。1842年，他发表了《微积分演算》一文，详尽讨论微积分基本原理和极限定义，并讨论了无穷序列及确定序列收敛的新规则。他曾从事当时称为“形式代数”的研究，其成果有助于对复数的性质给出一个完全的几何解释。

 

德·摩根的主要成就在逻辑方面，主要逻辑著作是《形式逻辑》（1847）。他在逻辑史上首先提出“论域”的概念，第一次明确用公式表达合取和析取的关系，现代逻辑称之为德·摩根律。

 

他还最先提出了关于“大多数”的推理。他对逻辑的最主要贡献在于开拓了形式逻辑的新领域，建立了关系逻辑，有的学者称他为“关系逻辑之父”。他对关系的种类和性质作了研究，并使用了一些他自己所创造的符号。

 

德·摩根提出了一些重要的关系逻辑规律，以及一些推理形式等。符号“/”是19世纪英国数学家德•摩根在1845年提出的．德•摩根是一个生性乐观，热爱生活，嗜好猜谜的人，享年65岁，每当有人问他年龄或出生时，他常风趣地答道：“我在x²年是x岁！”由此判断，他出生在______年．

 

43²=1849，符合题意；即他43岁时是1849年，则他的出生年份是1849-43=1806年。