习题-函数
习题
1. 设\(f:A\rightarrow B\)，\(A_0\subset A\)和\(B_0\subset B\)。
(a) 证明\(A_0\subset f^{-1}(f(A_0))\)，并且当\(f\)是单射时，式中包含关系可换为等号。
(b) 证明\(f(f^{-1}(B_0))\subset B_0\)，并且当\(f\)是满射时，式中包含关系可换为等号。
2. 设\(f:A\rightarrow B\)，并且对于\(i=0\)和1，\(A_i\subset A\)，\(B_i\subset B\)。证明\(f^{-1}\)保持集合的包含、并、交和差：
(a) \(B_0\subset B\Longrightarrow f^{-1}(B_0)\subset f^{-1}(B_1)\)。
(b) \(f^{-1}(B_0\cup B_1)=f^{-1}(B_0)\cup f^{-1}(B_1)\)。
(c) \(f^{-1}(B_0\cap B_1)=f^{-1}(B_0)\cap f^{-1}(B_1)\)。
(d) \(f^{-1}(B_0 - B_1)=f^{-1}(B_0) - f^{-1}(B_1)\)。
证明\(f\)仅保持集合的包含和并：
(e) \(A_0\subset A_1\Longrightarrow f(A_0)\subset f(A_1)\)。
(f) \(f(A_0\cup A_1)=f(A_0)\cup f(A_1)\)。
(g) \(f(A_0\cap A_1)\subset f(A_0)\cap f(A_1)\)。证明当\(f\)是单射时，式中包含关系\(\subset\)可换为等号。
(h) \(f(A_0-A_1)\supset f(A_0)-f(A_1)\)。证明当\(f\)是单射时，式中包含关系\(\supset\)可换为等号。
3. 证明习题2中的(b)、(c)、(f)、(g)小题对于任意并和任意交成立。
4. 设\(f:A\rightarrow B\)，\(g:B\rightarrow C\)。
(a) 若\(C_0\subset C\)，证明\((g\circ f)^{-1}(C_0)=f^{-1}(g^{-1}(C_0))\)。
(b) 若\(f\)和\(g\)都是单射，证明\(g\circ f\)也是一个单射。
(c) 若\(g\circ f\)是一个单射，试讨论\(f\)和\(g\)是否是单射？
(d) 若\(f\)和\(g\)都是满射，证明\(g\circ f\)也是一个满射。
(e) 若\(g\circ f\)是一个满射，试讨论\(f\)和\(g\)是否是满射？
(f)将从(b)-(e)各小题得到的结论总结为一个定理。
5. 集合\(C\)的恒等函数（identity function）一般记作\(i_C\)。函数\(i_C:C\rightarrow C\)定义为：对于任意\(x\in C\)，\(i_C(x)=x\)。对于函数\(f:A\rightarrow B\)，如果存在函数\(g:B\rightarrow A\)，使\(g\circ f=i_A\)，则称\(g\)为\(f\)的左逆（left inverse）。如果存在函数\(h:B\rightarrow A\)，使\(f\circ h = i_B\)，则称\(h\)为\(f\)的右逆（right inverse）。
(a) 证明：若\(f\)有左逆，则\(f\)是单射；若\(f\)有右逆，则\(f\)是满射。
(b) 举出一个有左逆而无右逆的函数的例子。
(c) 举出一个有右逆而无左逆的函数的例子。
(d) 是否存在有多个左逆的函数？是否存在有多个右逆的函数？
(e) 证明：若\(f\)既有左逆\(g\)，又有右逆\(h\)，则\(f\)是一一对应并且
6. 假设函数\(f:\mathbb{R}\rightarrow \mathbb{R}\)是通过式子\(f(x)=x^3-x\)来定义的。适当限制其定义域及改变值域得到一个一一的函数\(g\)。画出\(g\)和\(g^{-1}\)的图形（\(g\)有多种可能的选择）。
解答
1. 证明 (a) 若\(x\in A_0\)，则\(f(x)\in f(A_0)\)，由定义可知\(x\in f^{-1}(f(A_0))\)，故\(A_0\subset f^{-1}(f(A_0))\)。
设\(f\)为单射。若\(x\in f^{-1}(f(A_0))\)，则\(f(x)\in f(A_0)\)，故存在\(x'\in A_0\)，使得\(f(x')=f(x)\)。由\(f\)的单射性可知\(x'=x\)，故\(x\in A_0\)，\(A_0\supset f^{-1}(f(A_0))\)，结合上面的证明可知\(A_0=f^{-1}(f(A_0))\)。
(b) 若\(y\in f(f^{-1}(B_0))\)，则\(f^{-1}(\{y\})\cap f^{-1}(B_0)\ne \varnothing\)。取\(x\in f^{-1}(\{y\})\cap f^{-1}(B_0)\)，则\(y=f(x)\in B_0\)，故\(f(f^{-1}(B_0))\subset B_0\)。
设\(f\)为满射。若\(y\in B_0\)，由\(f\)的满射性可知，存在\(x\in f^{-1}(B_0)\)，使得\(f(x)=y\)。故\(y=f(x)\in f(f^{-1}(B_0))\)，由此可知\(f(f^{-1}(B_0))\supset B_0\)，结合上面的证明可知\(f(f^{-1}(B_0))= B_0\)。
$\square$
2. 证明 (a) 设\(B_0\subset B_1\)。对于任意\(x\in f^{-1}(B_0)\)，有\(f(x)\in B_0\)，进而\(f(x)\in B_1\)，故\(x\in f^{-1}(B_1)\)。由此可知\(B_0\subset B\Longrightarrow f^{-1}(B_0)\subset f^{-1}(B_1)\)。
(b) 等号两边条件的等价性如下：
(c) 等号两边条件的等价性如下：
(d) 等号两边条件的等价性如下：
(e) 设\(A_0\subset A_1\)。若\(y\in f(A_0)\)，则存在\(x\in A_0\)，使得\(y=f(x)\)。由包含关系可知\(x\in A_1\)，故\(y=f(x)\in f(A_1)\)。由此可知\(A_0\subset A_1\Longrightarrow f(A_0)\subset f(A_1)\)。
(f) 等号两边条件的等价性如下：
(g) 若\(y\in f(A_0\cap A_1)\)，则存在\(x\in A_0\cap A_1\)，使得\(y=f(x)\)。由于\(x\in A_0\)，故\(y=f(x)\in f(A_0)\)。类似地，我们可以得到\(y=f(x)\in f(A_1)\)。那么\(y\in f(A_0)\cap f(A_1)\)。由此可知\(f(A_0\cap A_1)\subset f(A_0)\cap f(A_1)\)。
设\(f\)为单射。若\(y\in f(A_0)\cap f(A_1)\)，则分别存在\(x_0\in A_0\)和\(x_1\in A_1\)，有\(y=f(x_0)=f(x_1)\)。由\(f\)的单射性可知\(x_0=x_1\)，不妨都记为\(x\)，则\(x\in A_0\cap A_1\)，\(y=f(x)\in f(A_0\cap A_1)\)。由此可知\(f(A_0\cap A_1)\supset f(A_0)\cap f(A_1)\)，结合上面的证明可知\(f(A_0\cap A_1) = f(A_0)\cap f(A_1)\)。
(h) 若\(y\in f(A_0)-f(A_1)\)，则\(y\in f(A_0)\)且\(y\notin f(A_1)\)。由此可知存在\(x_0\in A_0\)，使得\(y=f(x_0)\)；不存在\(x_1\in A_1\)，使得\(y=f(x_1)\)；故\(x_0\notin A_1\)，\(x_0\in A_0-A_1\)。由此可知\(y=f(x_0)\in f(A_0-A_1)\)，\(f(A_0-A_1)\supset f(A_0)-f(A_1)\)。
设\(f\)为单射。若\(y\in f(A_0 - A_1)\)，则存在\(x\in A_0-A_1\)，使得\(y=f(x)\)。故\(x\in A_0\)且\(x\notin A_1\)，由此可知\(f(x)\in f(A_0)\)，需要证明\(f(x)\notin f(A_1)\)。若\(f(x)\in f(A_1)\)，则存在\(x_1\in A_1\)，使得\(y=f(x)=f(x_1)\)。由\(f\)的单射性可知\(x_1=x\)，这与\(x_1\in A_1\)矛盾。故\(y=f(x)\in f(A_0)-f(A_1)\)，\(f(A_0-A_1)\subset f(A_0)-f(A_1)\)。结合上面的证明可知\(f(A_0-A_1) = f(A_0)-f(A_1)\)。
$\square$
3. 证明 (b') 下面证明以下等式成立
注意到以下等价关系成立
(c') 下面证明以下等式成立
注意到以下等价关系成立
(f') 下面证明以下等式成立
注意到以下等价关系成立
(g') 下面证明以下蕴含关系成立
注意到以下推导成立
$\square$
4. 证明 (a) 有以下等价关系成立
(b) 设\(f,g\)均为单射。若\((g\circ f)(x_1)=(g\circ f)(x_2)\)，那么\(g(f(x_1))=g(f(x_2))\)，由\(g\)的单射性可知\(f(x_1)=f(x_2)\)，又由\(f\)的单射性可知\(x_1=x_2\)，故\(g\circ f\)为单射。
(c) 由\(f:(0,1)\rightarrow \mathbb{R},f(x)=x\)，\(g:\mathbb{R}\rightarrow \mathbb{R},g(x)=x^2\)可知\(g\)不一定是单射，其中\(\mathbb{R}\)为实数集。下面证明\(f\)为单射。设\(g\circ f\)为单射。若\(f\)不为单射，那么存在\(a_1,a_2\in A\)，有\(a_1\ne a_2,f(a_1)=f(a_2)\)，进而\((g\circ f)(a_1)=g(f(a_1))=g(f(a_2))=(g\circ f)(a_2)\)，这与\(g\circ f\)的单射性矛盾。
(d) 设\(f,g\)均为满射。对任意\(c\in C\)，由\(g\)的满射性可知，存在\(b_0\in B\)，使得\(g(b_0)=B\)。又由\(f\)的满射性可知，存在\(a_0\in A\)，使得\(f(a_0)=b_0\)。那么有\((g\circ f)(a_0)=g(f(a_0))=g(b_0)=c\)。由此可知\(g\circ f\)为满射。
(e) 由\(f:\mathbb{R}\rightarrow \mathbb{R},f(x)=x^2\)，\(g:\mathbb{R}\rightarrow \overline{\mathbb{R}}_+,g(x)=|x|\)可知\(f\)不一定是满射，其中\(\mathbb{R}\)是实数集，\(\overline{\mathbb{R}}_+\)是非负实数集。下面证明\(g\)是满射。若\(g\circ f\)是满射，则对于任意\(c\in C\)，存在\(a_0\in A\)，使得\((g\circ f)(a_0)=g(f(a_0))=c\)。令\(b_0=f(a_0)\in B\)，那么对于任意\(c\in C\)，存在\(b_0\in B\)，使得\(g(b_0)=g(f(a_0))=c\)，由满射性的定义可知\(g\)是满射。
(f) 两个映射\(f,g\)均为单射（满射），是复合\(g\circ f\)为单射（满射）的充分条件。而复合\(g\circ f\)是单射（满射）的必要条件是\(f\)为单射（\(g\)为满射）。
$\square$
5. 解 (a) 若\(f\)有左逆\(g\)，则对于任意\(a_1,a_2\in A\)，若\(f(a_1)=f(a_2)\)，则\(a_1=i_A(a_1)=(g\circ f)(a_1)=g(f(a_1))=g(f(a_2))=(g\circ f)(a_2)=i_A(a_2)=a_2\)。由此可知\(f\)为单射。
若\(f\)有右逆\(h\)，则对于任意\(b\in B\)，\(f(h(b))=(f\circ h)(b)=i_B(b)=b\)。令\(a=h(b)\in A\)，则对于任意\(b\in B\)，存在\(a\in A\)，使得\(f(a)=f(h(b))=b\)，这说明\(f\)为满射。
(b) 函数\(f:\overline{\mathbb{R}}_+\rightarrow \mathbb{R},f(x)=x\)有左逆\(g:\mathbb{R}\rightarrow \overline{\mathbb{R}}_+,g(x)=|x|\)，易验证\(g\circ f\)是\(\overline{\mathbb{R}}_+\)上的恒等函数，其中\(\mathbb{R}\)是实数集，\(\overline{\mathbb{R}}_+\)是非负实数集。又\(f\)不是满射，结合(a)可知\(f\)没有右逆。
(c) 函数\(f:\mathbb{R}\rightarrow\overline{\mathbb{R}}_+,f(x)=x^2\)有右逆\(h:\overline{\mathbb{R}}_+\rightarrow\mathbb{R},h(x)=\sqrt{x}\)，易验证\(f\circ h\)是\(\overline{\mathbb{R}}_+\)上的恒等函数，其中\(\mathbb{R}\)是实数集，\(\overline{\mathbb{R}}_+\)是非负实数集。又\(f\)不是单射，结合(a)可知\(f\)没有左逆。
(d) 函数\(f_1:\overline{\mathbb{R}}_+\rightarrow \mathbb{R},f_1(x)=x\)有多个左逆\(g_1:\mathbb{R}\rightarrow \overline{\mathbb{R}}_+,g_1(x)=|x|\)，\(g_2:\mathbb{R}\rightarrow \overline{\mathbb{R}}_+,g_2(x)=x\)。函数\(f_2:\mathbb{R}\rightarrow\overline{\mathbb{R}}_+,f_2(x)=x^2\)有多个右逆\(h_1:\overline{\mathbb{R}}_+\rightarrow\mathbb{R},h_1(x)=\sqrt{x}\)，\(h_2:\overline{\mathbb{R}}_+\rightarrow\mathbb{R},h_2(x)=-\sqrt{x}\)。
(e) 由(a)可知，若\(f\)既有左逆\(g\)又有右逆\(h\)，则\(f\)是一个一一对应，存在逆\(f^{-1}:B\rightarrow A\)。那么对任意\(b\in B\)，\(g(b)=g(f(f^{-1}(b)))=(g\circ f)(f^{-1}(b))=i_A(f^{-1}(b))=f^{-1}(b)\)，\(f^{-1}(b) = f^{-1}(i_B(b))=f^{-1}((f\circ h)(b))=f^{-1}(f(h(b)))=h(b)\)。又\(g:B\rightarrow A,h:B\rightarrow A\)，故\(g=h=f^{-1}\)。
6. 解 函数\(f(x)=x^3-x\)的导函数为\(f'(x)=3x^2 - 1\)。由此可知函数\(f(x)\)在\((-\infty,-\frac{\sqrt{3}}{3})\)和\((\frac{\sqrt{3}}{3},+\infty)\)上单调递增，在\((-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})\)上单调递减。且\(f(x)\)在\(x=-\frac{\sqrt{3}}{3}\)处的极大值为\(\frac{2\sqrt{3}}{9}\)，在\(x=\frac{\sqrt{3}}{3}\)处的极小值为\(-\frac{2\sqrt{3}}{9}\)。为了保证\(g\)是一个一一对应，可将\(f\)限制在单调区间\((-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})\)上，其对应的值域应为\((-\frac{2\sqrt{3}}{9},\frac{2\sqrt{3}}{9})\)。\(g:(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})\rightarrow(-\frac{2\sqrt{3}}{9},\frac{2\sqrt{3}}{9})\)与\(g^{-1}:(-\frac{2\sqrt{3}}{9},\frac{2\sqrt{3}}{9})\rightarrow (-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})\)的图像如下所示。
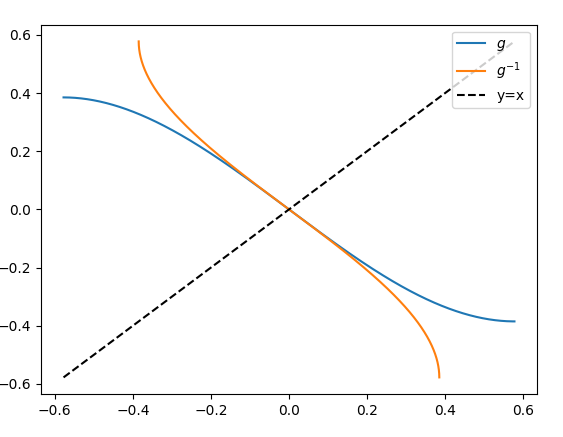$g$与$g^{-1}$的图像
浙公网安备 33010602011771号