基于NOMP和降维字典的杂波空时功率谱稀疏恢复算法matlab仿真

1.前言

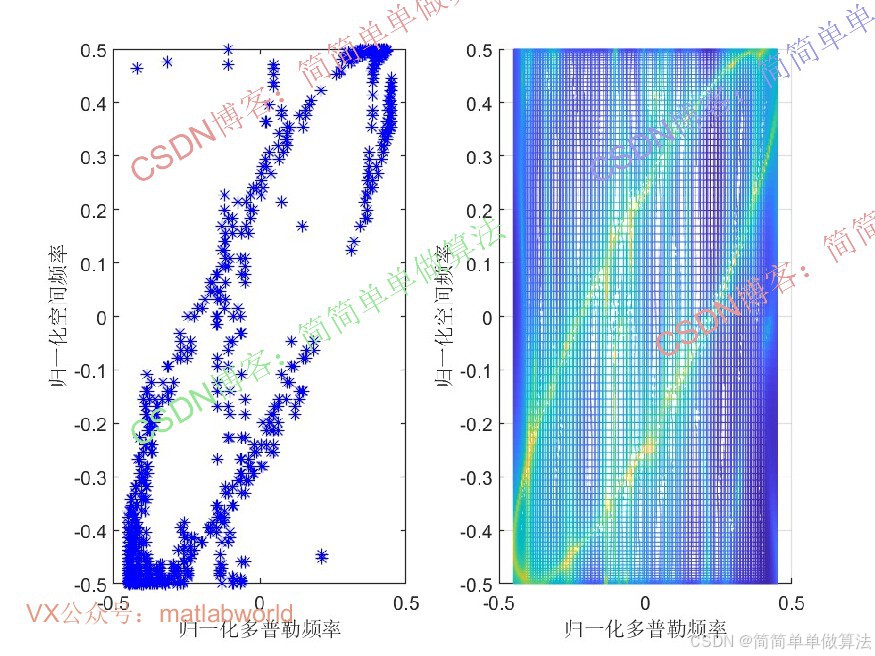
空时自适应处理（STAP）是抗杂波的核心技术，其关键在于准确估计杂波的空时功率谱。传统 STAP 方法（如样本协方差矩阵求逆，SMI）需满足 “样本数远大于自由度” 的要求，在小样本条件下性能显著下降。近年来，压缩感知（Compressive Sensing, CS）理论因其利用信号稀疏性实现低样本高效恢复的特性，被引入杂波功率谱估计领域。基于稀疏恢复的算法通过构建空时导向矢量字典，将功率谱估计转化为稀疏信号重构问题，显著降低了对训练样本数的依赖。

2.算法运行效果图预览

(完整程序运行后无水印)

 

3.算法运行软件版本

Matlab2024b(推荐)或者matlab2022a

4.部分核心程序

（完整版代码包含中文注释和操作步骤视频）

...............................................................
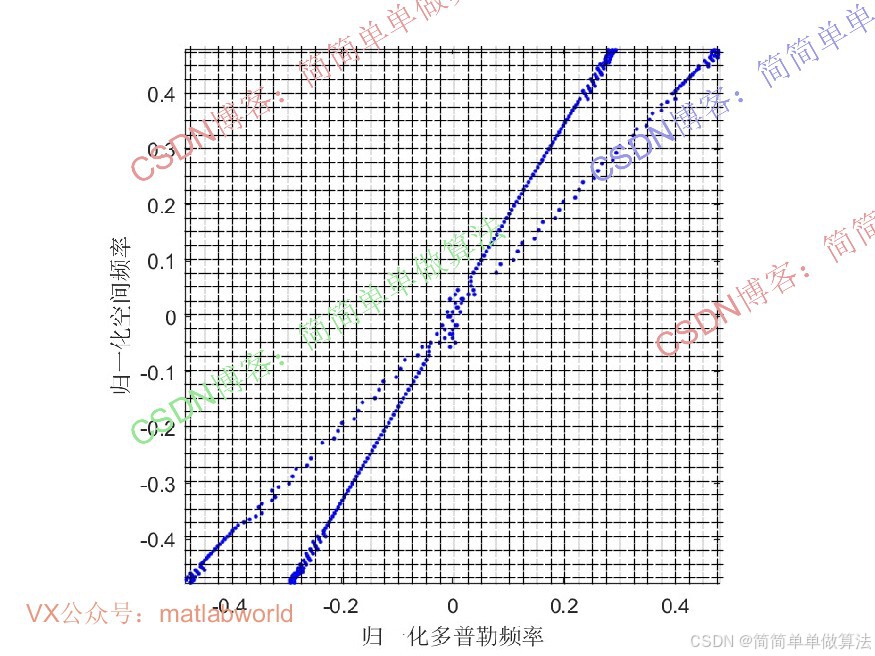
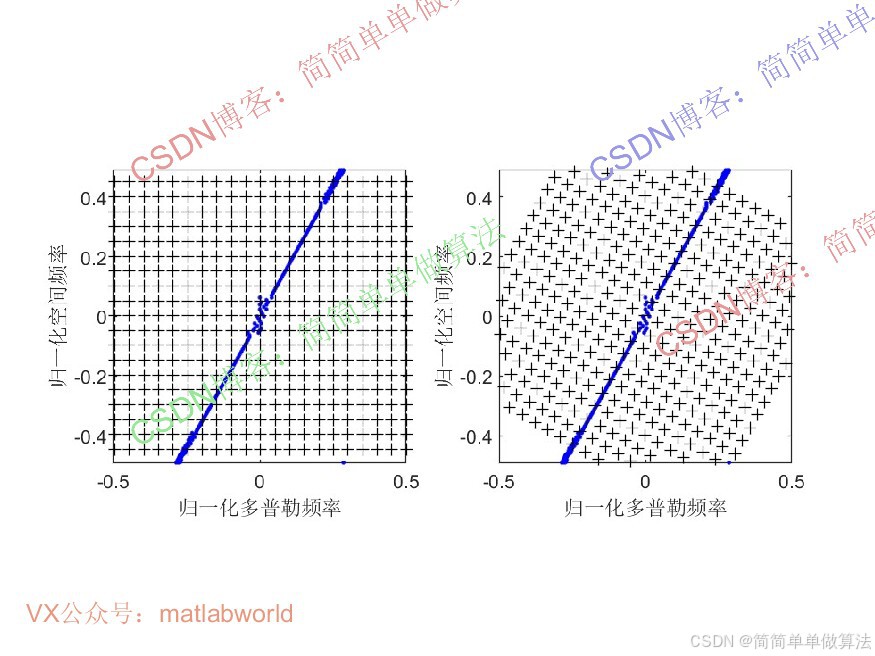
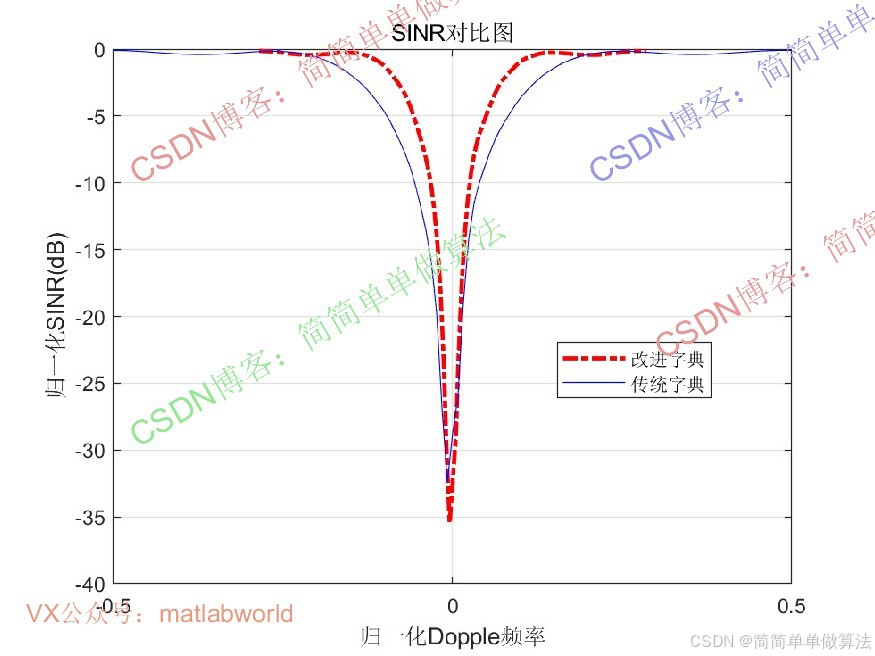
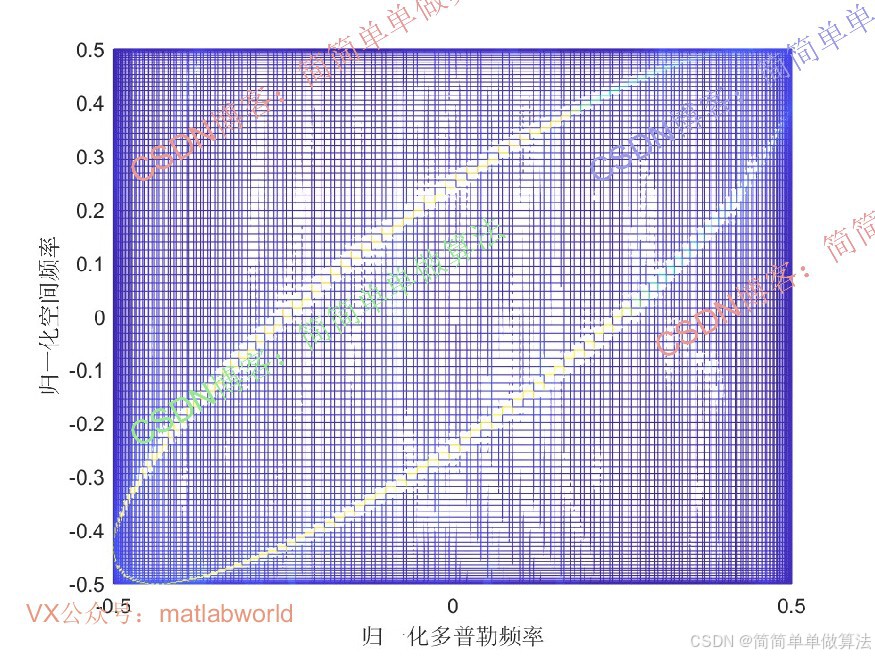
%杂波空时功率谱
 
[Rs,Cs] = size(Pmn1);
Pmn1s=zeros(Rs,Cs);
X=[];
Y=[];
Pmn1abs = 20*log10(abs(Pmn1));
Pmn1abs = Pmn1abs-min(min(Pmn1abs));
tmax=max(max(Pmn1abs));
for i = 1:Rs
    for j = 1:Cs
        if Pmn1abs(i,j)>0.45*tmax
           X=[X,vfd1(j)/pi];
           Y=[Y,sin(sita1(i))/2];
        end
    end
end
 
 
for ii = 1:Cm
    for jj = 1:Cm
        SS = kron(Va_fs(:,ii),Vb_fs(:,jj));
        W  = SS'*inv(R);
        SINR2(ii,jj) = W*SS/(SS'*SS);
    end
end
 
 
 
figure
subplot(121);
plot(X(10:10:end),Y(10:10:end),'b*');
xlabel('归一化多普勒频率');
ylabel('归一化空间频率');
 
subplot(122);
mesh(vfds/pi,sin(sita1)/2,20*log10(abs(Pmn1)));
hold on
xlabel('归一化多普勒频率');
ylabel('归一化空间频率');
grid on
view([0,90]);
save NOMP.mat
16_0240m

 

5.算法仿真参数

%杂波仿真参数
%阵元个数，发射和接收均为4
N_zy = 4;                   
%相干脉冲数
lmda = 1;   
M    = 32;  
%杂波干扰大小之杂噪比
CNR  = 15;                       
sita    = [-180:1.8:180]*pi/180;
[Rn,Cm] = size(sita);
 
%目标参数
DOAT     = -25;                
DopplerT = 0.4;                 
SNR      = 0;     

6.算法理论概述

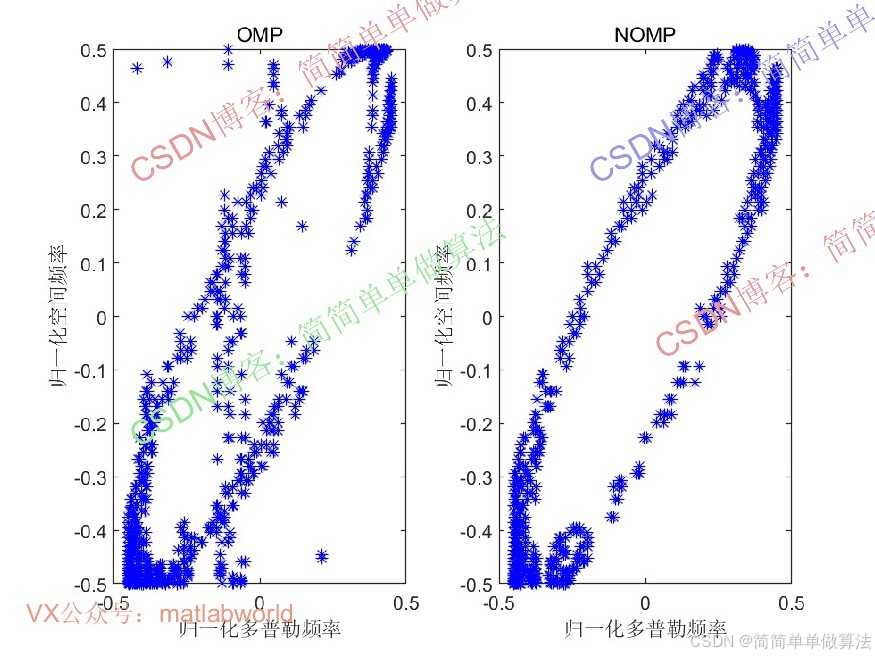
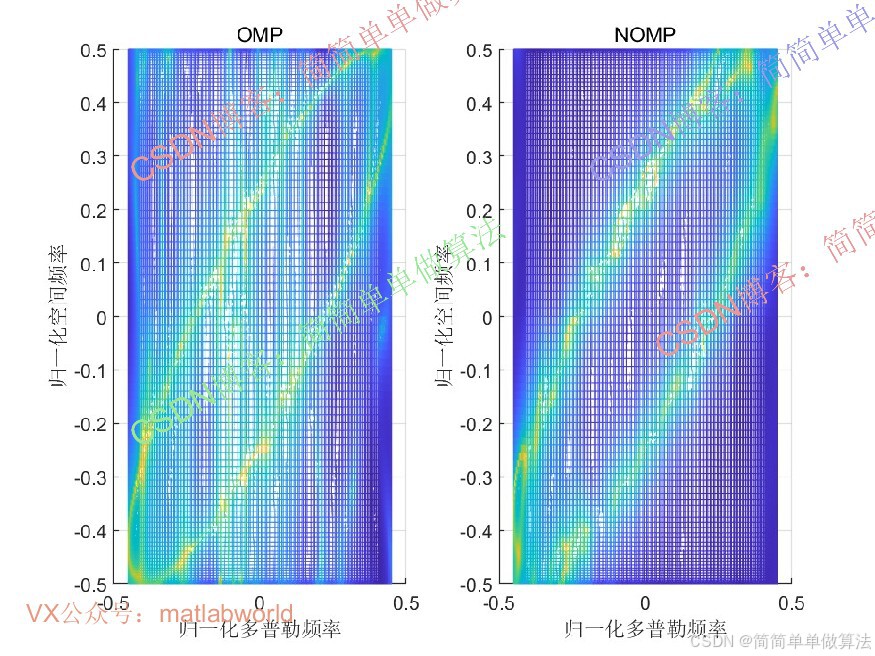
非正交匹配追踪（NOMP）是匹配追踪（MP）的改进算法，适用于非正交字典。其核心思想是通过迭代选择与残差相关性最大的原子，并更新系数直至残差能量低于阈值。与正交匹配追踪（OMP）不同，NOMP无需在每次迭代中对已选原子进行正交化，更适合处理降维后的非正交字典，兼具效率与重构精度。

基于NOMP和降维字典的杂波空时功率谱稀疏恢复算法，通过压缩感知框架利用杂波稀疏性，结合字典降维和非正交匹配追踪，实现了小样本条件下杂波功率谱的高效高精度估计。该算法降低了传统STAP对训练样本数和计算资源的依赖，适用于机载雷达等实时处理场景。