贝叶斯优化(Bayesian Optimization)深入理解
目前在研究Automated Machine Learning,其中有一个子领域是实现网络超参数自动化搜索,而常见的搜索方法有Grid Search、Random Search以及贝叶斯优化搜索。前两者很好理解,这里不会详细介绍。本文将主要解释什么是体统(沉迷延禧攻略2333),不对应该解释到底什么是贝叶斯优化。
I Grid Search & Random Search
我们都知道神经网络训练是由许多超参数决定的,例如网络深度,学习率,卷积核大小等等。所以为了找到一个最好的超参数组合,最直观的的想法就是Grid Search,其实也就是穷举搜索,示意图如下。
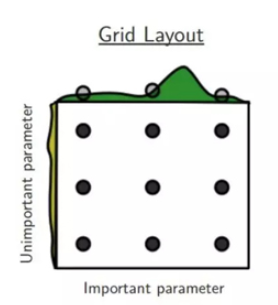
但是我们都知道机器学习训练模型是一个非常耗时的过程,而且现如今随着网络越来越复杂,超参数也越来越多,以如今计算力而言要想将每种可能的超参数组合都实验一遍(即Grid Search)明显不现实,所以一般就是事先限定若干种可能,但是这样搜索仍然不高效。
所以为了提高搜索效率,人们提出随机搜索,示意图如下。虽然随机搜索得到的结果互相之间差异较大,但是实验证明随机搜索的确比网格搜索效果要好。
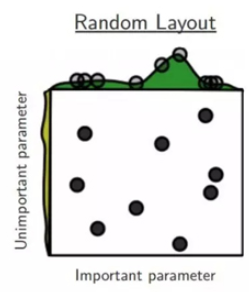
II Bayesian Optimization
假设一组超参数组合是\(X={x_1,x_2,...,x_n}\)(\(x_n\)表示某一个超参数的值),不同超参数会得到不同效果,贝叶斯优化假设超参数与最后我们需要优化的损失函数存在一个函数关系。
而目前机器学习其实是一个黑盒子(black box),即我们只知道input和output,所以很难确直接定存在什么样的函数关系,所以我们需要将注意力转移到一个我们可以解决的函数上去,下面开始正式介绍贝叶斯优化。
贝叶斯优化的大体思路如下:
假设我们有一个函数\(f:x→\Bbb{R}\),我们需要在\(x\subseteq X\)内找到
\(x^*=\underset{x\in X}{\operatorname{argmin}}f(x) \tag{1}\)
注意上面的\(x\)表示的是超参数,而不是输入数据。以图像分类任务为例,\(x\)可以是学习率,batch size等超参数的设置。而为了避免全文符号太多,所以将输入数据隐去了,换句话说\(f(x)\)等价于\(f(x|img)\)
当\(f\)是凸函数且定义域\(X\)也是凸的时候,我们可以通过已被广泛研究的凸优化来处理,但是\(f\)并不一定是凸的,而且在机器学习中\(f\)通常是expensive black-box function,即计算一次需要花费大量资源。那么贝叶斯优化是如何处理这一问题的呢?
1. 详细算法
Sequential model-based optimization (SMBO) 是贝叶斯优化的最简形式,其算法思路如下:

下面详细介绍一下上图中的算法:
1. Input:
- \(f\): 就是那个所谓的黑盒子,即输入一组超参数,得到一个输出值。
- \(X\):是超参数搜索空间等。
- \(D\):表示一个由若干对数据组成的数据集,每一对数组表示为\((x,y)\),\(x\)是一组超参数,\(y\)表示该组超参数对应的结果。
- \(S\):是Acquisition Function(采集函数),这个函数的作用是用来选择公式(1)中的\(x\),后面会详细介绍这个函数。
- \(\cal{M}\):是对数据集\(D\)进行拟合得到的模型,可以用来假设的模型有很多种,例如随机森林,Tree Parzen Estimators(想要了解这两种的可以阅读参考文献[1])等,但是本文主要介绍高斯模型。
2. InitSamples(f,x)→D
这一步骤就是初始化获取数据集\(\cal{D}={(x_1,y_1),...,(x_n,y_n)}\),其中\(y_i=f(x_i)\),这些都是已知的。
3. 循环选参数\(T\)次
因为每次选出参数\(x\)后都需要计算\(f(x)\),而正如前面介绍的每计算一次函数\(f\),都会消耗大量资源,所以一般需要固定选参次数(或者是函数评估次数)。
- \(p(y|x,D)←FITMODEL(M,D)\)
首先我们预先假设了模型\(M\)服从高斯分布,且已知了数据集\(D\),所以可以通过计算得出具体的模型具体函数表示。假设下图中的绿色实现就是基于数据集\(D\)经过计算后的服从高斯分布模型。可以看到Each additional band of green is another half standard deviation on the output distribution.

那么高斯分布是如何计算的呢?
因为我们已经假设\(f\)~\(GP(μ,K)\)。 (GP:高斯过程,μ:均值 K:协方差kernel,)。所以预测也是服从正态分布的,即有\(p(y|x,D)=\cal{N}(y|\hat{μ},\hat{σ}^2)\)
- \(x_i←\underset{x\in X}{\operatorname{argmax}}S(X,p(y|X,D))\)
现在已经将假设的模型计算出来了,那么下一步我们需要基于假设模型的基础上选择满足公式(1)的参数了,也就是选择\(X\),那么如何选择呢?这就涉及到了Acquisition Function,为了让文章篇幅更易阅读,想了解Acquisition Function移步到文末。
- \(y_i←f(x_i)\)
既然参数选出来了,那么当然就是要计算咯。例如我们通过上述步骤已经选出了一组超参数\(x_i\),那么我们下一步就是将超参数带入网络中去进行训练,最后得到输出\(y_i\)。这一步骤虽然expensive,但是没办法还是得走啊。
- \(D←D \bigcup{(x_i,y_i)}\)
更新数据集。
2. Acquisition Function
Acquisition Function的选择可以有很多种,下面将分别介绍不同的AC function。
1) Probability of improvement
假设\(f'=min \, f\),这个\(f'\)表示目前已知的\(f\)的最小值。
然后定义utility function如下:
其实也可以把上面的\(u(x)\)理解成一个reward函数,如果f(x)不大于f'就有奖励,反之没有。
probability of improvement acquisition function定义为the expected utility as a function of x:
之后只需要求出\(a(x)\)的最大值即可求出基于高斯分布的满足要求的\(x\)。
2) Expected improvement
上面的AC function有个缺点就是找到的\(x\)可能是局部最优点,所以有了Expected improvement。\(f'\)的定义和上面一样,即\(f'=min \, f\)。utility function定义如下:
因为我们最初的目的是找到使得f(x)最小的x,所以这个utility function的含义很好理解,即接下来找到的\(f(x)\)比已知最小的\(f'\)越小越好,然后选出小的程度最大的那个\(f(x)\)和\(f'\)之间的差距的绝对值作为奖励,如果没有更小的那么奖励则为0.
AC function定义如下:
通过计算使得\(a_{EI}\)值最大的点即为最优点。
上式中有两个组成部分。要使得上式值最大则需要同时优化左右两个部分:
- 左边需要尽可能的减少\(μ(x)\)
- 右边需要尽可能的增大方差(或协方差)\(K(x,x)\)
但是二者并不同能是满足,所以这是一个exploitation-exploration tradeoff。
3) Entropy search

4) Upper confidence bound

Reference
- [1] Sigopt.com. Bayesian Optimization Primer (2018). [online] Available at: https://sigopt.com/static/pdf/SigOpt_Bayesian_Optimization_Primer.pdf [Accessed 26 Oct. 2018].
- [2] Cse.wustl.edu. Bayesian Optimization (2018). [online] Available at: https://www.cse.wustl.edu/~garnett/cse515t/spring_2015/files/lecture_notes/12.pdf [Accessed 26 Oct. 2018].
- [3] Anon,How does Bayesian optimization work? (2018). [online] Available at: https://www.quora.com/How-does-Bayesian-optimization-work [Accessed 26 Oct. 2018].


 浙公网安备 33010602011771号
浙公网安备 33010602011771号