「算法笔记」后缀树
一、后缀树
前置知识:字典树(Trie)。
后缀树:所有后缀 \(S[i\sim n]\,(1\leq i\leq n)\) 组成的 Trie 树。
本质不同的子串个数可以达到 \(\mathcal{O}(n^2)\) 级别,故节点数为 \(\mathcal{O}(n^2)\),与枚举原串的每个子串等价。
叶子节点只有不超过 \(\mathcal{O}(n)\) 个,因此大部分节点都有且仅有一个孩子。
(每分叉一次就会多一个叶子节点。一开始根节点算一个叶子节点,最后有不超过 \(n\) 个叶子节点,也就是多了不超过 \(n-1\) 个叶子节点。所以分叉的点数一定小于等于 \(n-1\)。那么其他的节点都是不分叉的,因此大部分节点都有且仅有一个孩子。)
大部分节点都 只有一个孩子,考虑合并这样的链信息。即我们可以 缩掉仅有一个孩子的节点。就像这样:
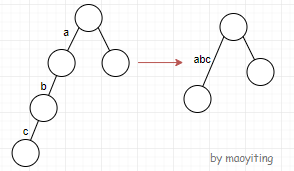
这样新的树中的节点数就变成 \(\mathcal{O}(n)\) 的了。
所以后缀树是所有后缀组成的,经过 信息压缩 后的 Trie 树。
二、虚树
1. 定义
对于树 \(T=(V,E)\),给定关键点 \(S⊆V\),则可以定义 虚树 \(T'=(V',E')\)。
-
对于节点集合 \(V'⊆V\) ,使得 \(u\in V'\) 当且仅当 \(u\in S\),或者 \(∃x,y\in S\),使得 \(\text{LCA}(x,y)=u\)。(即 \(u\in V'\) 当且仅当 \(u\) 为关键点或关键点的 \(\text{LCA}\))
-
对于边集 \(E'\),\((u,v)\in E'\),当且仅当 \(u,v∈V'\),且 \(u\) 是 \(v\) 在 \(V'\) 中深度最浅的祖先。
与之前所说的联系:假如把所有叶子节点当做关键点的话,任意两个叶子节点的 \(\text{LCA}\) 一定是分叉点,那么 \(V'\) 就是所有的叶子节点以及分叉点组成的集合。
而 \(E'\) 其实就是把不分叉的链缩成一条边后的边集(即 \(E'\) 中的一条边对应着一条没有子树的链)。这与我们之前说的「缩掉仅有一个孩子的节点」对应。
2. 构建虚树
考虑增量法,每次向虚树中增加一个关键点。
按 DFS 序依次加入 \(u\in S\),栈维护 右链(栈中相邻的两个节点在虚树上也是相邻的,并且栈中节点 DFS 序单调递增)。
每加入一个关键点 \(u\),设上一个关键点为 \(v\),令 \(\text{LCA}(u,v)=w\),将栈顶 \(dep_x>dep_w\) 的弹栈,加入 \(w,u\) 即为新的右链。
(若栈顶存在 \(dep_x=dep_w\),则不加入 \(w\)。)

在此过程中维护每个点的父节点,最终连边即可得到 \(E′\)。
设 \(n=|S|\)。时间复杂度:\(\mathcal{O}(n\log n)\)。
三、SA 构建后缀树
后缀数组 + 虚树。
虚树的角度:
-
按字典序 DFS,则节点排序相当于对后缀进行排序,亦即后缀数组。
-
求出后缀数组后,即可用单调栈维护右链了。
-
\(\text{LCA}\) 对应了两个节点的 \(\text{LCP}\),因此可以 RMQ。
时间复杂度:\(\mathcal{O}(n\log n)\)。
(不会 SAM 就可以用 SA+虚树 的方法啦)
四、SAM 构建后缀树
我们同样可以使用 后缀自动机 来构建后缀树:
定理:后缀自动机的 parent 树为反串后缀树。
正串的 SAM 维护的是原字符串所有前缀的后缀(可以考虑 SAM 增量法的构造过程)。那么同理,反串的 SAM,维护的就是所有后缀的前缀,可以得到所有后缀构成的 Trie,即后缀树。
建出反串的 SAM 之后,就会直接得到后缀树。
时间复杂度: \(\mathcal{O}(n|\sum|)\) 或 \(\mathcal{O}(n\log n)\)。
五、Ukkonen 算法
Ukkonen 算法可以 \(\mathcal{O}(n)\) 构建后缀树。
(反正我不会 QAQ,可以康 这里)


