「算法笔记」长链剖分

修改于 2023 年不知道哪个月。

2020 年写的长剖入门（已折叠）
一、长链剖分

长链剖分本质上就是另外一种链剖分方式。

对于每一个节点：

  • 定义 重子节点 表示其子节点中子树 深度最大 的子节点。如果有多个子树深度最大的子节点，取其一。如果没有子节点，就无重子节点。

  • 定义 轻子节点 表示剩余的子节点。

  • 从这个节点到重子节点的边为 重边。到其他轻子节点的边为 轻边。

  • 若干条首尾衔接的重边构成 长链。把落单的节点也当作长链，那么整棵树就被剖分成若干条互不相交的长链。

树上每个节点都属于且仅属于一条长链 。长链剖分实现方式和重链剖分类似。

void dfs1(int x,int fa){
    dep[x]=dep[fa]+1,mx[x]=dep[x],f[x]=fa;    //dep(x) 表示节点 x 在树上的深度，f(x) 表示节点 x 在树上的父亲，mx(x) 表示节点 x 子树中的最大深度 
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa) continue;
        dfs1(y,x);
        if(mx[y]>mx[son[x]]) son[x]=y,mx[x]=mx[y];    //son(x) 表示节点 x 的重儿子 
    }
}
void dfs2(int x,int topf){
    top[x]=topf,len[x]=mx[x]-dep[top[x]]+1;    //top(x) 表示节点 x 所在长链的顶部结点（深度最小） ，len(x) 表示节点 x 所在长链的长度 
    if(son[x]) dfs2(son[x],topf);    //优先对重儿子进行 DFS 
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y!=f[x]&&y!=son[x]) dfs2(y,y);
    } 
}
二、一些性质

性质一：对树长链剖分后，树上所有长链的长度和为 \(\mathcal{O(n)}\)。

  • 因为每个点仅属于一条长链，只会被计算一次，所以长链长度的总和为 \(\mathcal{O(n)}\)。

性质二：任意一个节点 \(x\) 的 \(k\) 级祖先 \(y\) 所在长链的长度一定大于等于 \(k\)。

  • 如果 \(y\) 所在的长链的长度小于 \(k\)，那么它所在的链一定不是长链，因为 \(y\to x\) 这条链显然更优，那么 \(y\) 所在的长链长度至少为 \(k\)，性质成立；反之，\(y\) 所在长链的长度大于等于 \(k\)，性质成立。

性质三：一个节点跳跃长链到根节点，跳跃的次数最多为 \(\mathcal{O(\sqrt{n})}\)。

  • 如果一个节点 \(x\) 从一条长链跳到了另外一条长链上，那么跳跃到的这条长链的长度不会小于之前的长链长度。最坏情况下，链长分别为 \(1,2,\cdots,\sqrt{n}\)，也就是最多跳跃 \(\sqrt{n}\) 次。
三、长链剖分优化 DP
1. CF1009F Dominant Indices

题目大意：给定一棵以 \(1\) 为根，\(n\) 个节点的树。设 \(d(u,x)\) 为 \(u\) 子树中到 \(u\) 距离为 \(x\) 的节点数。

对于每个点，求一个最小的 \(k\)，使得 \(d(u,k)\) 最大。\(1\leq n\leq 10^6\)。

Solution：

令 \(f_{i,j}\) 表示节点 \(i\) 的子树内，到 \(i\) 距离为 \(j\) 的节点数量。

显然 \(f_{u,0}=1,f_{u,i}=\sum\limits_{v\in son(u)} f_{v,i-1}\)。这样直接暴力转移的时间复杂度为 \(\mathcal{O}(n^2)\)。

考虑用长链剖分优化。在维护信息的过程中，先 \(\mathcal{O}(1)\) 继承重儿子的信息，再暴力合并其余轻儿子的信息。

具体地，对于每一个节点 \(u\)，先对它的重儿子 \(v\) 做 DP，转移时直接 继承 重儿子的 DP 数组和答案。当然观察 DP 式子可以发现这里需要错一位，因为 \(v\) 子树内「到 \(v\) 距离为 \(i\) 的节点」与 \(u\) 的距离为 \(i+1\)。所以可以在继承后，将当前节点的 DP 数组前面插入一个元素 \(1\)（即 \(f_{u,0}=1\)），表示当前节点。接下来对它的轻儿子 做 DP，将所有轻儿子的 DP 数组暴力和当前节点的 DP 数组合并。

因为每个点仅属于一条长链，且一条长链只会在链顶位置作为轻儿子暴力合并一次，所以复杂度线性。

在「\(\mathcal{O}(1)\) 继承重儿子的信息」这点上有不同的实现方式。

vector 实现： 
#include<bits/stdc++.h>
#define int long long
using namespace std; 
const int N=1e6+5;
int n,x,y,cnt,hd[N],to[N<<1],nxt[N<<1],len[N],son[N],ans[N];
vector<int>f[N];    //这里的 vector 是倒序存储的，因为要在继承重儿子的信息后，要将当前节点的 DP 数组最前面插入一个元素，而 push_back 的复杂度优于 pop_front，倒序存储就可以直接使用 push_back 
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
int get(int x,int id){    //由于 vector 是倒序存储的，此处将 vector 正序存储的位置转化为倒序存储的位置 
    return len[x]-id-1;
}
void dfs1(int x,int fa){
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa) continue;
        dfs1(y,x);
        if(len[y]>len[son[x]]) son[x]=y;
    }
    len[x]=len[son[x]]+1;
}
void dfs2(int x,int fa){
    if(son[x]) dfs2(son[x],x),swap(f[x],f[son[x]]),ans[x]=ans[son[x]]+1;    //继承重儿子的信息。这里的继承直接用 swap 而不是复制，swap 在时间和空间上都更优（swap 交换 vector 的时间复杂度为 O(1)）。 
    f[x].push_back(1);    //push_back 的复杂度优于 pop_front
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||y==son[x]) continue;
        dfs2(y,x);
        for(int j=1;j<=len[y];j++){
            f[x][get(x,j)]+=f[y][get(y,j-1)];    //暴力合并轻儿子的信息 
            if(f[x][get(x,j)]>f[x][get(x,ans[x])]||(f[x][get(x,j)]==f[x][get(x,ans[x])]&&j<ans[x])) ans[x]=j;    //更新答案
        }
    }
    if(f[x][get(x,ans[x])]==1) ans[x]=0;    //f[x][0]=1,f[x][ans[x]]=1，0 显然更优
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        add(x,y),add(y,x);
    }
    dfs1(1,0),dfs2(1,0);
    for(int i=1;i<=n;i++)
        printf("%lld\n",ans[i]);
    return 0;
}
指针实现：我们只对每一条长链的顶端节点申请内存，让一条长链上的所有节点公用一片空间。具体地，对节点 \(u\) 申请了内存之后，设 \(v\) 是 \(u\) 的重儿子，我们就把 \(f_u\) 数组的起点（的指针）加一作为 \(f_v\) 数组的起点（的指针）。具体见代码。

#include<bits/stdc++.h>
#define int long long
using namespace std; 
const int N=1e6+5;
int n,x,y,cnt,hd[N],to[N<<1],nxt[N<<1],len[N],son[N],ans[N],*f[N],tmp[N],*id=tmp;
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void dfs1(int x,int fa){
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa) continue;
        dfs1(y,x);
        if(len[y]>len[son[x]]) son[x]=y;
    }
    len[x]=len[son[x]]+1;
}
void dfs2(int x,int fa){ 
    f[x][0]=1;
    if(son[x]) f[son[x]]=f[x]+1,dfs2(son[x],x),ans[x]=ans[son[x]]+1;    //继承重儿子的信息。f[son[x]]=f[x]+1: 共享内存，这样之后，f[son[x]][i] 会被存到 f[x][i+1]  
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||y==son[x]) continue;
        f[y]=id,id+=len[y],dfs2(y,x);    //分配内存。为 y 节点申请内存，大小等于以 y 为顶端的长链的长度。申请的内存要能装下一条长链。 
        for(int j=1;j<=len[y];j++){
            f[x][j]+=f[y][j-1];    //暴力合并轻儿子的信息 
            if(f[x][j]>f[x][ans[x]]||(f[x][j]==f[x][ans[x]]&&j<ans[x])) ans[x]=j;    //更新答案 
        }
    }
    if(f[x][ans[x]]==1) ans[x]=0;    //f[x][0]=1,f[x][ans[x]]=1，0 显然更优 
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        add(x,y),add(y,x);
    }
    dfs1(1,0),f[1]=id,id+=len[1],dfs2(1,0);    //在 DP 开始前先为以树根为顶端的长链申请内存 
    for(int i=1;i<=n;i++)
        printf("%lld\n",ans[i]);
    return 0;
}

非 vector 非指针实现：

考虑 dfs 一遍给每个点分配一个 $pos_x$ 表示 $f_{x,0}$ 在我们开的 f[N] 中的位置（即我们不用指针写，开一个一维数组 f[N]，然后将 $f_{x,i}$ 对应到这个一维数组中去），优先对重儿子递归分配（换句话说，这个位置就是 dfs 时优先访问重儿子得到的 DFS 序）。考虑 dp 递归上来的时候重儿子的 $f_{son_x}$ 就没有用了，这时可以让这些内存为 $f_x$ 所用，而且重儿子是最深的，内存肯定刚好够用，而重儿子的 $pos_{son_x}$ 刚好就是 $pos_x+1$，那么就自动实现了“右移一格”的操作！具体来说，$f_{son_x,i}$ 在一维数组中的位置是 $pos_{son_x}+i$，$f_{x,i}$ 在一维数组中的位置是 $pos_x+i$，因为 $pos_{son_x}=pos_x+1$，所以 $f_{x,i+1}$ 对应的就是 $pos_x+(i+1)=pos_{son_x}+i$，也就是 $f_{son_x,i}$。 
#include<bits/stdc++.h>
#define int long long
using namespace std; 
const int N=1e6+5;
int n,x,y,len[N],son[N],ans[N],f[N],tot,pos[N];
vector<int>v[N]; 
void dfs1(int x,int fa){
    for(int y:v[x])
        if(y!=fa) dfs1(y,x),son[x]=(len[y]>len[son[x]]?y:son[x]);
    len[x]=len[son[x]]+1;
}
void dfs2(int x,int fa){
    pos[x]=++tot;
    if(son[x]) dfs2(son[x],x);
    for(int y:v[x])
        if(y!=fa&&y!=son[x]) dfs2(y,x);
}
void dfs3(int x,int fa){ 
    if(son[x]) dfs3(son[x],x),ans[x]=ans[son[x]]+1;
    f[pos[x]]=1;
    for(int y:v[x]){
        if(y==fa||y==son[x]) continue;
        dfs3(y,x); 
        for(int i=1;i<=len[y];i++){
            f[pos[x]+i]+=f[pos[y]+i-1];
            if(f[pos[x]+i]>f[pos[x]+ans[x]]||(f[pos[x]+i]==f[pos[x]+ans[x]]&&i<ans[x])) ans[x]=i;
        }
    }
    if(f[pos[x]+ans[x]]==1) ans[x]=0;
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        v[x].push_back(y),v[y].push_back(x);
    }
    dfs1(1,0),dfs2(1,0),dfs3(1,0);
    for(int i=1;i<=n;i++)
        printf("%lld\n",ans[i]);
    return 0;
}
2. BZOJ 4543 [POI2014]Hotel 加强版

题目大意：给定一棵 \(n\) 个节点的树，在树上选 \(3\) 个点，要求两两距离相等，求方案数。\(1\leq n\leq 10^5\)。

Solution：

令 \(f_{u,i}\) 表示以 \(u\) 为根的子树中，距离 \(u\) 为 \(i\) 的节点个数。\(g_{u,i}\) 表示以 \(u\) 为根的子树中，两个点 \(x,y\) 到其 \(\text{lca}\) 的距离为 \(d\)，且 \(\text{lca}\) 到 \(u\) 的距离为 \(d-i\) 的方案数。

转移：\(f_{u,i}=\sum\limits_{v\in son(u)}f_{v,i-1},g_{u,i}=\sum\limits_{v\in son(u)}g_{v,i+1}+f_{u,i}\times f_{v,i-1}\)。可以画图理解。

求出了 \(f\) 和 \(g\)，那么就能求出答案了（首先令 \(ans=\sum\limits_{u} g_{u,0}\)）：

  • 1. 在 \(u\) 的子树中选两个点，与 \(v\) 中的点拼：\(ans=ans+g_{u,i}\times f_{v,i-1}\)。

  • 2. 在 \(v\) 的子树中选两个点，与 \(u\) 中的点拼：\(ans=ans+f_{u,i}\times g_{v,i+1}\)。

如图，以第一种情况为例（第二种情况同理）。

暴力转移的时间复杂度为 \(\mathcal{O}(n^2)\)。然后用长链剖分优化成 \(\mathcal{O}(n)\) 即可。

同样是继承重儿子的信息，再暴力合并其余轻儿子的信息。

由于 \(g\) 数组转移的特殊，下标的变化很玄学，使用 vector 的写法 细节较多，使用 指针 分配内存的方法就可以减少细节量。

把 \(f_u\) 数组的起点（的指针）加一作为 \(f_v\) 数组的起点（的指针），\(g_u\) 数组的起点（的指针）减一作为 \(g_v\) 数组的起点（的指针）。\(f_{v}=f_{u}+1,g_{v}=g_{u}-1\)。

发现 \(g\) 的更新是反过来的，为了避免出错可以 多开点空间。顺便放一个 Dls 写的非 vector 非指针 的写法。

#include<bits/stdc++.h>
#define int long long
using namespace std; 
const int N=1e5+5;
int n,x,y,cnt,hd[N],to[N<<1],nxt[N<<1],len[N],son[N],*f[N],*g[N],tmp[N<<2],*id=tmp,ans;
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void dfs1(int x,int fa){
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa) continue;
        dfs1(y,x);
        if(len[y]>len[son[x]]) son[x]=y;
    }
    len[x]=len[son[x]]+1;
}
void dfs2(int x,int fa){
    if(son[x]) f[son[x]]=f[x]+1,g[son[x]]=g[x]-1,dfs2(son[x],x);    //继承重儿子的信息 
    f[x][0]=1,ans+=g[x][0]; 
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||y==son[x]) continue;
        f[y]=id,id+=len[y]<<1,g[y]=id,id+=len[y]<<1,dfs2(y,x);
        for(int j=1;j<=len[y];j++){     //暴力合并轻儿子的信息 
            ans+=g[x][j]*f[y][j-1]+f[x][j-1]*g[y][j];
            g[x][j]+=f[x][j]*f[y][j-1];
        } 
        for(int j=1;j<=len[y];j++)
            f[x][j]+=f[y][j-1],g[x][j-1]+=g[y][j];
    }
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        add(x,y),add(y,x);
    }
    dfs1(1,0),f[1]=id,id+=len[1]<<1,g[1]=id,id+=len[1]<<1,dfs2(1,0);
    printf("%lld\n",ans);
    return 0;
}
小总结：长链剖分可以把维护子树中 只与深度有关 的信息优化到线性。

长链剖分优化 DP 的实现方式就是，长链剖分后，在维护信息的过程中，先 \(\mathcal{O}(1)\) 继承重儿子的信息，再暴力合并其余轻儿子的信息。

一、长链剖分

重儿子：子树深度最大的儿子。

显然的性质：

  1. 所有长链长度之和 \(\mathcal O(n)\)。

  2. 任意 \(x\) 的 \(k\) 级祖先 \(y\) 所在长链长度 \(\geq k\)。

  3. 任意一点向上跳跃长链次数最多 \(\mathcal O(\sqrt n)\)。

    （切换长链时长链长度肯定越来越长，最坏链长 \(1,2,\cdots,\sqrt n\)）

有时可以带权，用于维护贪心。注意如果是按边分的，一条长链的贡献要加上链顶的父边权值。带权时性质 3 不成立。

二、树上 k 级祖先

P5903 【模板】树上 k 级祖先

给出一棵 \(n\) 个节点的有根树，\(q\) 次询问点 \(x\) 的 \(k\) 级祖先。

\(2\leq n\leq 5\times 10^5\)，\(1\leq q\leq 5\times 10^6\)。

倍增预处理 \(f_{x,j}\) 表示 \(x\) 的 \(2^j\) 级祖先。查 \((x,k)\) 时：

  1. 找到最大的 \(j\) 使得 \(2^j<k\)，\(x'\gets f_{x,j}\)，\(k'\gets k-2^j\)。

  2. \(x'\) 所在长链的长度 \(d\) 一定 \(\geq 2^j\)（长剖性质 2），而 \(x'\) 最多再向上跳 \(2^j-1\) 步。

  3. 对于每个链顶 \(tp\) 预处理 \(tp\) 向上 \(len_{tp}\) 个祖先和向下 \(len_{tp}\) 个长儿子，链总长 \(\mathcal O(n)\) \(\Rightarrow\) 这部分复杂度 \(\mathcal O(n)\)。

    从 \(x'\) 向上跳，不可能跳到 \(top_{x'}\) 的 \(len_{top_{x'}}\) 级祖先上方。所以可以 \(x'\) 跳到 \(top_{x'}\) 再根据预处理的数组调整。

时间复杂度 \(\mathcal O(n\log n)-\mathcal O(1)\)。

void dfs(int x,int fa){
	dep[x]=dep[fa]+1; 
	for(int i=0;i<=19;i++) f[x][i+1]=f[f[x][i]][i]; 
	for(int y:v[x])
		if(y!=fa) f[y][0]=x,dfs(y,x),son[x]=len[y]>len[son[x]]?y:son[x];
	len[x]=len[son[x]]+1; 
}
void dfs2(int x,int tp){
	top[x]=tp;
	if(x==tp){
		for(int i=0,j=x;i<=len[x];i++) up[x].push_back(j),j=f[j][0];
		for(int i=0,j=x;i<=len[x];i++) dn[x].push_back(j),j=son[j]; 
	} 
	if(son[x]) dfs2(son[x],tp);
	for(int y:v[x])
		if(y!=f[x][0]&&y!=son[x]) dfs2(y,y);
}
int kth(int x,int k){
	if(!k) return x;
	int t=__lg(k);
	x=f[x][t],k-=1<<t,k-=dep[x]-dep[top[x]],x=top[x];
	return k>=0?up[x][k]:dn[x][-k];
}

upd on 2023.3.15：还有个重剖 \(\mathcal O(n)-\mathcal O(\log n)\) 做法。跳重链过程中若链顶到 \(x\) 的距离 \(\geq k\)，说明 \(k\) 级祖先在这条重链上。然后由于重链上 dfs 序连续，可直接得到答案。

1. CF504E Misha and LCP on Tree（*3000）

2022.1.5

给出一棵 \(n\) 个节点的树，每个节点有一个小写字母。\(m\) 次询问，每次询问树上 \(a\to b\) 和 \(c\to d\) 组成的字符串的最长公共前缀。

\(1\leq n\leq 3\times 10^5\)，\(1\leq m\leq 10^6\)。

二分 LCP 长度，哈希 check。check 的过程中要用到求一个点的 \(k\) 级祖先，由于 \(m\leq 10^6\)，使用倍增跳 fa 会 TLE，需使用长链剖分。复杂度 \(\mathcal O(m\log n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5,mod=1e9+7;
int n,m,x,y,f[N][25],len[N],son[N],top[N],dep[N],lg[N],c=131;
long long p[N],hu[N],hd[N],inv[N];
char s[N];
vector<int>v[N],up[N],dn[N];
void dfs1(int x,int fa){
	dep[x]=dep[fa]+1;
	hd[x]=(hd[fa]*c%mod+s[x])%mod,hu[x]=(hu[fa]+s[x]*p[dep[x]]%mod)%mod;
	for(int i=0;i<=19;i++) f[x][i+1]=f[f[x][i]][i]; 
	for(int y:v[x])
		if(y!=fa) f[y][0]=x,dfs1(y,x),son[x]=len[y]>len[son[x]]?y:son[x];
	len[x]=len[son[x]]+1; 
}
void dfs2(int x,int tp){
	top[x]=tp;
	if(x==tp){
		for(int i=0,j=x;i<=len[x];i++) up[x].push_back(j),j=f[j][0];
		for(int i=0,j=x;i<=len[x];i++) dn[x].push_back(j),j=son[j]; 
	} 
	if(son[x]) dfs2(son[x],tp);
	for(int y:v[x])
		if(y!=f[x][0]&&y!=son[x]) dfs2(y,y);
}
int kth(int x,int k){
	if(!k) return x;
	int t=lg[k];
	x=f[x][t],k-=(1<<t),k-=dep[x]-dep[top[x]],x=top[x];
	return k>=0?up[x][k]:dn[x][-k];
}
int lca(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=20;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
	if(x==y) return x;
	for(int i=20;i>=0;i--)
		if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	return f[x][0];
}
signed main(){
	scanf("%d%s",&n,s+1),p[0]=inv[0]=1,lg[0]=-1;
	for(int i=1;i<=n;i++) p[i]=p[i-1]*c%mod,inv[i]=inv[i-1]*190839696%mod,lg[i]=lg[i>>1]+1;
	for(int i=1;i<n;i++){
		scanf("%d%d",&x,&y);
		v[x].push_back(y),v[y].push_back(x);
	}
	dfs1(1,0),dfs2(1,1),scanf("%d",&m);
	while(m--){
		int a,b,c,d,l1,l2;
		scanf("%d%d%d%d",&a,&b,&c,&d),l1=lca(a,b),l2=lca(c,d);
		int l=1,r=min(dep[a]+dep[b]-dep[l1]*2,dep[c]+dep[d]-dep[l2]*2)+1,ans=0;
		auto query=[&](int x,int y,int lca,int k){
			auto get=[&](int x,int y,int len,int op){return op==1?(hd[x]-hd[y]*p[len]%mod+mod)%mod:(hu[x]-hu[y]+mod)%mod*inv[len]%mod;};
			int pl=dep[x]-dep[lca]+1,pr=dep[y]-dep[lca];
			if(k<=pl) return get(x,k==pl?f[lca][0]:kth(x,k),k,1);
			return (get(x,f[lca][0],pl,1)+get(kth(y,pl+pr-k),lca,dep[lca]+1,2)*p[pl]%mod)%mod; 
		};
		while(l<=r){
			int mid=(l+r)/2;
			if(query(a,b,l1,mid)==query(c,d,l2,mid)) ans=mid,l=mid+1;
			else r=mid-1;
		}
		printf("%d\n",ans);
	}
	return 0;
}

三、优化 DP

优化与深度有关的 DP。

利用指针 \(\mathcal O(1)\) 继承重儿子信息，再暴力合并轻儿子。根据链总长 \(\mathcal O(n)\) 的性质，复杂度 \(\mathcal O(n)\)。

注意：

  1. 注意下标不要越界，比如下标 \(\geq len_x\) 就认为值为 \(0\) 等等需要特判！！越界不仅会导致 RE，若取了数组中别的位置的值就 wa 了。

  2. 可以多开一点避免越界。直接 f[y]=id,id+=len[y] 开到的是 \(f_{y,0\sim len_y-1}\)。

    开大之后注意数组别开小。

  3. \(\mathcal O(\sum_{x=top_x}len_x)=\mathcal O(n)\)，\(\mathcal O(\sum len_x)\) 没有保证！

技巧：

  1. 对于一条路径，在 \(\text{lca}\) 处统计它的贡献。

  2. DP 有时要先后缀和优化。前缀和看似要数据结构维护，实际上可以改为 总数 - 后缀和。

    好处？加入 \(f_y\) 后，重新维护前缀和的后缀是 \(\mathcal O(len_x)\) 的，而重新维护后缀和的前缀是 \(\mathcal O(len_y)\) 的，枚举量就和加入 \(f_y\) 复杂度一样了。

  3. 类似重链剖分，优先遍历重儿子，这样每条长链的 DFS 序连续，为继承重儿子提供便利。不仅仅用于指针，有时还可以用数据结构维护 DFS 序，自动继承重儿子。

1. CF1009F Dominant Indices（*2300）

2020.12.24

给出一棵 \(n\) 个节点的树。设 \(d(x,k)\) 为 \(x\) 子树中到 \(x\) 距离为 \(k\) 的节点数。

对于每个点 \(x\)，求一个最小的 \(k\)，使得 \(d(x,k)\) 最大。

\(n\leq 10^6\)。

int *f[N],tmp[N],*id=tmp;
void dfs(int x,int fa){
	for(int y:v[x])
		if(y!=fa) dfs(y,x),son[x]=len[y]>len[son[x]]?y:son[x];
	len[x]=len[son[x]]+1; 
}
void dfs2(int x,int fa){
	f[x][0]=1;
	if(son[x]) f[son[x]]=f[x]+1,dfs2(son[x],x),ans[x]=ans[son[x]]+1;	 //继承重儿子的信息。f[son[x]]=f[x]+1: 共享内存，这样之后，f[son[x]][i] 会被存到 f[x][i+1]
	for(int y:v[x]) if(y!=fa&&y!=son[x]){
		f[y]=id,id+=len[y],dfs2(y,x);	//分配/申请内存
		for(int i=1;i<=len[y];i++){ 
			f[x][i]+=f[y][i-1];
			if(f[x][i]>f[x][ans[x]]||(f[x][i]==f[x][ans[x]]&&i<ans[x])) ans[x]=i; 
		} 
	}
	if(f[x][ans[x]]==1) ans[x]=0;
} 
//main 函数里：dfs(1,0),f[1]=id,id+=len[1],dfs2(1,0)

2. P5904 [POI2014]HOT-Hotels 加强版

2020.12.25

给出一棵 \(n\) 个节点的树，求选三个互不相同的点并且两两距离相等的方案数。

\(1\leq n\leq 10^5\)。

考虑三个点的位置关系。树上问题可以在 \(\text{lca}\) 处统计答案。

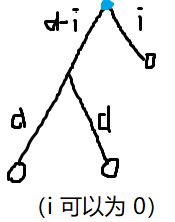
image

设 \(f_{x,i}\) 表示 \(x\) 子树内与 \(x\) 距离为 \(i\) 的点的个数；\(g_{x,i}\) 表示 \(x\) 子树内 \(dis(p,\text{lca}(p,q))=dis(q,\text{lca}(p,q))=dis(\text{lca}(p,q),x)+i\) 的无序对 \((p,q)\) 的个数。

\(f_{x,i}=\sum_{y\in son_x} f_{y,i-1}\)，\(g_{x,i}=\sum_{v\in son_x}g_{y,i+1}+f_{x,i}\times f_{y,i-1}\)（这里的 \(f_x\) 还没从 \(f_y\) 转移）。

void dfs2(int x,int fa){
	if(son[x]) f[son[x]]=f[x]+1,g[son[x]]=g[x]-1,dfs2(son[x],x); 
	f[x][0]=1,ans+=g[x][0];
	for(int y:v[x]) if(y!=fa&&y!=son[x]){
		f[y]=id,id+=len[y]<<1,g[y]=id,id+=len[y]<<1,dfs2(y,x);
		for(int i=1;i<=len[y];i++){ 
			ans+=g[x][i]*f[y][i-1]+f[x][i-1]*g[y][i];
			g[x][i]+=f[x][i]*f[y][i-1];
		} 
		for(int i=1;i<=len[y];i++) f[x][i]+=f[y][i-1],g[x][i-1]+=g[y][i];
	}
}

3. 小练习

2022.8.1

求树上长度 \(\leq k\) 的路径条数。

\(n\leq 10^6\)。

对于一条路径，在 \(\text{lca}\) 处统计它的贡献。

继承重儿子，加入轻儿子。对每个轻儿子 \(y\)，枚举 \(i\leq len_y\)，将 \(\sum_{j+i+1\leq k}f_{x,j}\times f_{y,i}\) 加入答案，统计完答案后再 \(f_{x,i+1}\gets f_{x,i+1}+f_{y,i}\)。

要求 \(f_{x,0\sim k-i-1}\) 的和，前缀和看似要线段树，实际上可以改为计算 总数 - 后缀和，维护后缀和。每次改一个位置，维护后缀和的一段前缀枚举量是 \(len_y\)。

时间复杂度 \(\mathcal O(n)\)。

4. P3899 [湖南集训]更为厉害

2022.1.5

给出一个 \(n\) 个节点的有根树，\(m\) 次询问，每次给出 \(a,k\)，求有多少有序三元组 \((a,b,c)\,(a\neq b\neq c)\)，满足 \(a,b\) 都是 \(c\) 的祖先且 \(dis(a,b)\leq k\)。

\(n,q\leq 3\times 10^5\)。

显然 \(a,b\) 是祖先关系。

  1. \(b\) 为 \(a\) 的祖先：方案数 \(\min(dep_a-1,k)\times (sz_a-1)\)。

  2. \(a\) 为 \(b\) 的祖先：方案数 \(\sum_{b\in subtree_a}[dis(a,b)\leq k](sz_b-1)\)。可以简单树上主席树 \(\mathcal O(n\log n)\)，这里考虑长剖 \(\mathcal O(n)\)。

    设 \(f_{x,i}\) 表示 \(\sum_{p\in subtree_x}[dis(x,p)=i](sz_p-1)\)，转移 \(f_{x,i}=\sum_{y\in son_x}f_{y,i-1}\)，\(f_{x,0}=sz_x-1\)。前缀和改成 总量 - 后缀和，维护 \(suf_{x,i}\) 表示 \(f_{x,i}\) 的后缀和即可。

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,m,x,y,k,dep[N],len[N],son[N],sz[N];
long long *f[N],tmp[N],*id=tmp,ans[N];
vector<int>v[N];
vector<pair<int,int> >q[N];
void dfs1(int x,int fa){
	dep[x]=dep[fa]+1,sz[x]=1;
	for(int y:v[x])
		if(y!=fa) dfs1(y,x),sz[x]+=sz[y],son[x]=len[y]>len[son[x]]?y:son[x];
	len[x]=len[son[x]]+1; 
}
void dfs2(int x,int fa){
	if(son[x]) f[son[x]]=f[x]+1,dfs2(son[x],x);
	for(int y:v[x]) if(y!=fa&&y!=son[x]){
		f[y]=id,id+=len[y],dfs2(y,x);
		for(int i=1;i<=len[y];i++) f[x][i]+=f[y][i-1];
	}
	f[x][0]=f[x][1]+sz[x]-1;
	for(auto p:q[x]){
		int k=p.first,i=p.second;
		ans[i]+=1ll*(sz[x]-1)*min(k,dep[x]-1)+f[x][1]-(k+1<len[x]?f[x][k+1]:0);
	}
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++)
		scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
	for(int i=1;i<=m;i++)
		scanf("%d%d",&x,&k),q[x].push_back({k,i});
	dfs1(1,0),f[1]=id,id+=len[1],dfs2(1,0);
	for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
	return 0;
}

5. P4292 [WC2010]重建计划

2022.1.6

给出一棵 \(n\) 个节点的树，边有边权，求边数 \(\in[l,r]\) 之间的一条路径，使得平均权值最大。

\(n\leq 10^5\)，边权 \(\leq 10^6\)。

01 分数规划：二分 \(mid\) check 是否存在边数 \(\in[l,r]\) 的路径 \(S\) 使得 \(\frac{\sum_{e\in S}v_e}{|S|}\geq mid\Rightarrow \sum_{e\in S}(v_e-mid)\geq 0\)。将边权都减 \(mid\)，转化为求边数 \(\in[l,r]\) 的路径边权和最大是多少。

在路径两端的 \(\text{lca}\) 处统计：设 \(f_{x,i}\) 表示 \(x\) 向下延伸 \(i\) 条边的路径边权和最大值，\(f_{x,i}=\max_{y\in son_x}f_{y,i-1}+w_{x,y}\)，可以长剖优化。

合并两边时处理边数限制：对 DFS 序建立线段树，\(f_{x,i}\) 存到线段树第 \(dfn_x+i\) 个位置（每条长链的 DFS 序连续，好处是自动实现“继承重儿子”）。左半边枚举 \(i\)，右半边查询线段树 \([dfn_x+l-i,dfn_x+r-i]\) 的最大值，枚举完再线段树上当前子树的贡献。

优化：直接记 \(f_{x,i}\) 表示从 \(x\) 往下延伸 \(i\) 条边得到的点中，到根的边权和最大值。这样继承重儿子时不用区间加。

时间复杂度 \(\mathcal O(n\log^2 n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,l,r,x,y,z,num,dfn[N],son[N],len[N],val[N];
double mx[N<<2],del,f[N],dis[N],ans;
vector<pair<int,int> >v[N];
void modify(int p,int l,int r,int pos,double v){
	if(l==r){mx[p]=max(mx[p],v);return ;}
	int mid=(l+r)/2;
	if(pos<=mid) modify(p<<1,l,mid,pos,v);
	else modify(p<<1|1,mid+1,r,pos,v);
	mx[p]=max(mx[p<<1],mx[p<<1|1]); 
}
double query(int p,int l,int r,int lx,int rx){
	if(lx>rx) return -1e18;
	if(l>=lx&&r<=rx) return mx[p];
	int mid=(l+r)/2; double ans=-1e18;
	if(lx<=mid) ans=max(ans,query(p<<1,l,mid,lx,rx));
	if(rx>mid) ans=max(ans,query(p<<1|1,mid+1,r,lx,rx));
	return ans; 
}
void dfs1(int x,int fa){ 
	for(auto p:v[x]){ 
		int y=p.first;
		if(y==fa) continue;
		dfs1(y,x);
		if(len[y]>len[son[x]]) son[x]=y,val[son[x]]=p.second;
	} 
	len[x]=len[son[x]]+1; 
}
void dfs(int x,int fa){
	dfn[x]=++num,modify(1,1,n,dfn[x],dis[x]);
	if(son[x]) dis[son[x]]=dis[x]+val[son[x]]-del,dfs(son[x],x);
	for(auto p:v[x]){
		int y=p.first;
		if(y==fa||y==son[x]) continue;
		dis[y]=dis[x]+p.second-del,dfs(y,x);
		for(int i=0;i<=len[y];i++) f[i]=query(1,1,n,dfn[y]+i,dfn[y]+i);
		for(int i=1;i<=min(len[y],r);i++)
			ans=max(ans,f[i-1]+query(1,1,n,dfn[x]+l-i,min(dfn[x]+r-i,dfn[x]+len[x]-1))-2*dis[x]);
		for(int i=1;i<=len[y];i++) modify(1,1,n,dfn[x]+i,f[i-1]);
	}
	ans=max(ans,query(1,1,n,dfn[x]+l,min(dfn[x]+r,dfn[x]+len[x]-1))-dis[x]);
}
signed main(){
	scanf("%d%d%d",&n,&l,&r);
	for(int i=1;i<n;i++){
		scanf("%d%d%d",&x,&y,&z);
		v[x].push_back({y,z}),v[y].push_back({x,z});
	}
	dfs1(1,0);
	double l=0,r=1e6;
	while(l+1e-5<r){
		double mid=(l+r)/2;
		for(int i=1;i<=(n<<2);i++) mx[i]=-1e18;
		num=0,ans=-1e18,del=mid,dfs(1,0);
		if(ans>=0) l=mid;
		else r=mid;
	}
	printf("%.3lf\n",l);
	return 0;
}

6. 小练习 Ⅱ

2023.2.6

给出一棵 \(n\) 个节点的树和 \(D\)，求有多少个子集 \(S\)（可以是空集）使得 \(S\) 中任意两个点的树上距离都 \(\geq D\)。求方案数 \(\bmod 998244353\)。

\(1\leq D\leq n\leq 2\times 10^6\)。

将两个所选点的限制在 \(\text{lca}\) 处考虑。

设 \(f_{x,i}\) 表示子树 \(x\) 内最浅的所选点离 \(x\) 的距离为 \(i\) 的方案数。转移 \(f_{x,i}\times f_{y,j}\to f'_{x,\min(i,j+1)}\,(i+(j+1)\geq D)\)。 枚举 \(\min\) 由 \(i\) 贡献还是由 \(j+1\) 贡献，设 \(f_{x,i}\) 的后缀和为 \(suf_{x,i}\)。

\[f'_{x,i}\gets f_{x,i}\times \sum_{j+1\geq i\land i+(j+1)\geq D}f_{y,j}=f_{x,i}\times suf_{y,\max(i-1,D-i-1)}\\ f'_{x,j+1}\gets f_{y,j}\times \sum_{i>j+1\land i+(j+1)\geq D}f_{x,i}=f_{y,j}\times suf_{x,\max(j+2,D-j-1)}\\ \Rightarrow f'_{x,i}=f_{x,i}\times suf_{y,\max(i-1,D-i-1)}+f_{y,i-1}\times suf_{x,\max(i+1,D-i)} \]

注意按 \(j+1\geq i\) 和 \(i\geq j+1\) 考虑会算重，区别于最优化问题，必须一个 \(\geq\) 一个 \(>\)！

由于 \(suf_{y,j},f_{y,j}\) 当 \(j\geq len_y\) 时一定是 \(0\)，这样限制起来单次枚举的 \(i\) 是 \(\mathcal O(len_y)\) 的。

长链剖分优化即可，\(f_x,suf_x\) 的下标范围是 \([0,len_x)\)。时间复杂度 \(\mathcal O(n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5,mod=998244353;
int n,d,x,son[N],len[N],*f[N],*suf[N],tmp[N<<1],*id=tmp;
vector<int>v[N];
void dfs(int x){
	for(int y:v[x])
		dfs(y),son[x]=len[y]>len[son[x]]?y:son[x];
	len[x]=len[son[x]]+1;
}
void dfs2(int x){
	if(son[x]) f[son[x]]=f[x]+1,suf[son[x]]=suf[x]+1,dfs2(son[x]);
	for(int y:v[x]) if(y!=son[x]){
		f[y]=id,id+=len[y],suf[y]=id,id+=len[y],dfs2(y);
		for(int i=1;i<=len[y];i++){
			int fi=(f[x][i]+f[y][i-1])%mod;	//!!!
			if(max(i-1,d-i-1)<len[y])
				fi=(fi+1ll*f[x][i]*suf[y][max(i-1,d-i-1)])%mod;
			if(max(i+1,d-i)<len[x])
				fi=(fi+1ll*f[y][i-1]*suf[x][max(i+1,d-i)])%mod;
			f[x][i]=fi;
		}
		for(int i=len[y];i>=0;i--)
			suf[x][i]=(f[x][i]+(i+1<len[x]?suf[x][i+1]:0))%mod;
	}
	f[x][0]=1+(d<len[x]?suf[x][d]:0);	//选 x
	suf[x][0]=(f[x][0]+(1<len[x]?suf[x][1]:0))%mod;
}
signed main(){
	scanf("%d%d",&n,&d);
	for(int i=2;i<=n;i++)
		scanf("%d",&x),v[i-x].push_back(i);
	dfs(1),f[1]=id,id+=len[1],suf[1]=id,id+=len[1],dfs2(1);
	printf("%d\n",(suf[1][0]+1)%mod);	//+1：算上空集
	return 0;
}

四、维护贪心

边权和贡献最大的问题可以往长链剖分贪心这个角度考虑。

技巧：

  1. 经典结论：选一个点能覆盖它到根的所有点。选 \(k\) 个点，覆盖的最大点权和就是前 \(k\) 条长链长度之和，选择的就是这 \(k\) 条长链的末端。

1. BZOJ#3252. 攻略

2022.1.5

给出一棵 \(n\) 个节点的树，点有点权 \(a_i\)。要求选定 \(k\) 个叶子节点，使得根节点到这 \(k\) 个叶子节点的所有路径的并的点权和最大。

\(n\leq 2\times 10^5\)，\(1\leq a_i\leq 2^{31}-1\)。

考虑带权的长链剖分，来实现“每次选一条点权和最大的路径，然后将路径上的点权清零”。

取剖出的链的前 \(k\) 条即可。时间复杂度 \(\mathcal O(n\log n)\)。

据说证明可以考虑建出网络流模型，不会发生退流操作。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,k,x,y,a[N],tot,son[N],fa[N],top[N];
long long len[N],b[N],ans;
vector<int>v[N];
void dfs1(int x){
	for(int y:v[x])
		if(y!=fa[x]) fa[y]=x,dfs1(y),son[x]=len[y]>len[son[x]]?y:son[x];
	len[x]=len[son[x]]+a[x]; 
}
void dfs2(int x,int tp){
	top[x]=tp;
	if(x==tp) b[++tot]=len[x];
	if(son[x]) dfs2(son[x],tp);
	for(int y:v[x])
		if(y!=fa[x]&&y!=son[x]) dfs2(y,y);
}
signed main(){
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<n;i++)
		scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
	dfs1(1),dfs2(1,1);
	sort(b+1,b+1+tot,greater<long long>());
	for(int i=1;i<=k;i++) ans+=b[i];
	printf("%lld\n",ans);
	return 0;
}

2. CF526G Spiders Evil Plan（*3300）

2022.1.6

给出一棵 \(n\) 个节点的无根树，边有边权。

\(q\) 次询问，每次给出 \(x,y\)，要求选择 \(y\) 条路径，使得这些路径的并是包含 \(x\) 的连通块，求并的最大边权和。

\(1\leq n,q\leq 10^5\)，\(1\leq w_i\leq 10^3\)，强制在线。

先不考虑包含 \(x\)：

  • 显然选的路径两端是叶子，要选 \(2y\) 个叶子。

    一个经典结论：\(k\) 个叶子的无根树，可以构造出 \(\lceil\frac k 2\rceil\) 条路径（一定是下界）覆盖所有边。

  • 性质：若根被选且 \(x\) 子树中有叶子被选，则 \(x\) 所在长链一定出现在连通块。

  • 如果枚举根，按上一题从大到小取长链即可。注意由于按边划分，长链的贡献要算上链顶的父边权值。

    实际上，直径的某端一定作为叶子被选，可以分别以直径的两端为根计算然后取最大值。

考虑包含 \(x\)：

  • 根必选。若前 \(2y-1\) 条长链已经包含 \(x\) 是最好的；否则考虑调整法，调整的方案只有两种：

    1. 第 \(2y-1\) 条长链不选，转而选取 \(x\) 所在长链。
    2. 第 \(2y-1\) 条长链选，找到离 \(x\) 最近的长链，把它最下面一段替换成 \(x\) 所在长链。

    实现时，将长链排名放在点上，倍增。

时间复杂度 \(\mathcal O(n\log n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,q,x,y,z,lst,d[N],pos;
vector<pair<int,int> >v[N];
struct tree{ 
	int rt,tot,dep[N],mx[N],f[N][25],son[N],top[N],rk[N],s[N];
	pair<int,int>a[N];
	void dfs1(int x){
		for(int i=0;i<=19;i++) f[x][i+1]=f[f[x][i]][i]; 
		for(auto p:v[x]){ 
			int y=p.first,z=p.second; 
			if(y==f[x][0]) continue;
			f[y][0]=x,mx[y]=dep[y]=dep[x]+z,dfs1(y);
			if(mx[y]>mx[x]) son[x]=y,mx[x]=mx[y];
		} 
	}
	void dfs2(int x,int tp){
		top[x]=tp;
		if(x==tp) a[++tot]={mx[x]-dep[f[x][0]],x};
		if(son[x]) dfs2(son[x],tp);
		for(auto p:v[x]){ 
			int y=p.first;
			if(y!=f[x][0]&&y!=son[x]) dfs2(y,y);
		} 
	}
	void init(int x){
		rt=x,dfs1(rt),dfs2(rt,rt);
		sort(a+1,a+1+tot,greater<pair<int,int> >());
		for(int i=1;i<=tot;i++) rk[a[i].second]=i,s[i]=s[i-1]+a[i].first;
		for(int i=1;i<=n;i++) rk[i]=rk[top[i]];
	}
	int query(int x,int y){
		auto get=[&](int x,int k){
			for(int i=20;i>=0;i--) if(rk[f[x][i]]>k) x=f[x][i];
			return f[x][0];
		};
		if((y=y*2-1)>tot) return s[tot];
		if(rk[x]<=y) return s[y];
		return max(s[y-1]+mx[x]-dep[get(x,y-1)],s[y]+mx[x]-mx[get(x,y)]);
	}
}t1,t2; 
void dfs(int x,int fa){
	if(d[x]>d[pos]) pos=x;
	for(auto p:v[x]){
		int y=p.first,z=p.second;
		if(y!=fa) d[y]=d[x]+z,dfs(y,x);
	}
}
signed main(){
	scanf("%d%d",&n,&q);
	for(int i=1;i<n;i++){
		scanf("%d%d%d",&x,&y,&z);
		v[x].push_back({y,z}),v[y].push_back({x,z});
	}
	dfs(1,0),t1.init(pos),d[pos]=0,dfs(pos,0),t2.init(pos);
	while(q--){
		scanf("%d%d",&x,&y),x=(x+lst-1)%n+1,y=(y+lst-1)%n+1;
		printf("%d\n",lst=max(t1.query(x,y),t2.query(x,y)));
	}
	return 0;
}
posted @ 2020-12-25 19:45  maoyiting  阅读(4522)  评论(0)    收藏  举报