大白话解释逻辑回归

记得在我学了线性回归之后的一段时间里，我觉得这个玩意太好用了，可以对世界上很多东西都进行预测，以至于一想到预测就想着拿点数据来进行回归。后来才知道，很多事情不是一条简单的直线可以拟合的。后来又知道，其实线性回归只要稍作修改，还是可以拟合这个世界上大部分事情的。是不是有点绕？其实原因很简单，很多事情看起来是非线性的，但是可以映射到一个线性的形状，对于这个映射之后的结果，我们可以进行线性回归。如果不清楚这个映射是什么意思，那请继续看下去。

假设我们现在要对一个人是否患肺癌进行判断，我们的方法是对胸部做CT，然后量其中阴影部分（肿瘤）的直径。没有比较无法直接判断，所以我们去查了10000条做过类似检查的病人案例，作为我们的样本。在我们的这个例子中，阴影的大小就是我们的样本特征值X，患肺癌的概率是P。我们希望找到一个方法，能让我们在知道了x的大小后，计算出p的大小（现实往往要复杂得多）。p是概率，应该在0和1之间。显然，我们不能用一条直线来拟合样本，为什么呢？首先，我们可以获得样本，只能是一个x对应一个“是否得病”的y，而不是一个概率。得病的样本，y用1来表示，没得病的样本，y用0来表示。其次，p的范围只有0到1，而一条直线显然拟合结果会是负无穷到正无穷。在一个x的合理的定义域内，如果想用一条直线去拟合p，就会导致这条直线必为经过原点和（max（\(x_{i}\)),1）的对角线。一旦我们要检测的样本x值超过了样本点x的最大值，我们会惊奇得发现预测的得病概率超过了100%！显然这不是我们想要的。并且在整个定义域范围内，概率呈现了线性的变化，这和我们的预期也不一样，因为通常阴影大小超过一定值，我们就会觉得肿瘤大点或小点只是一个严重程度的差别，基本上99%的概率是患肺癌了（1%的概率可能是CT机器坏了-。-）。但是，我们也不可以通过减小斜率来让这条回归线更平缓，因为当我们没有查出阴影时（即x=0），应当认为我们的担心是多余的，没有患肺癌，此时的p也就是截距项必然为0，回归线经过原点。这样的回归线太过于局限和粗糙，效果不会太好。

那我们要怎么做才可以对这个案例进行建模呢？首先，我们使用“发生概率除以未发生的概率”，即p/（1-p）来表示一件事发生的相对概率，称之为odds（“几率”）。可以看到当概率接近1是，几率的大小接近于无穷，这就打开了回归线的上限，我们不用担心太大的样本导致概率超过100%了，因为我们总是可以通过映射将正无穷的odds转换为一个接近100%的p。然后，我们再处理下限问题，对这个p/（1-p）取对数。这个结果称之为“对数几率”，在数轴上的映射为负无穷到正无穷。这，就可以是我们线性回归的结果了。

\[ln(p/(1-p)) = \omega^{T}·\chi + b \]

这里的p和1-p，分别代表了x在特定值时y=1和y=0的概率。求解这个方程，用x的表达式来表示p和1-p，我们得到了条件概率形式的对数几率回归方程：

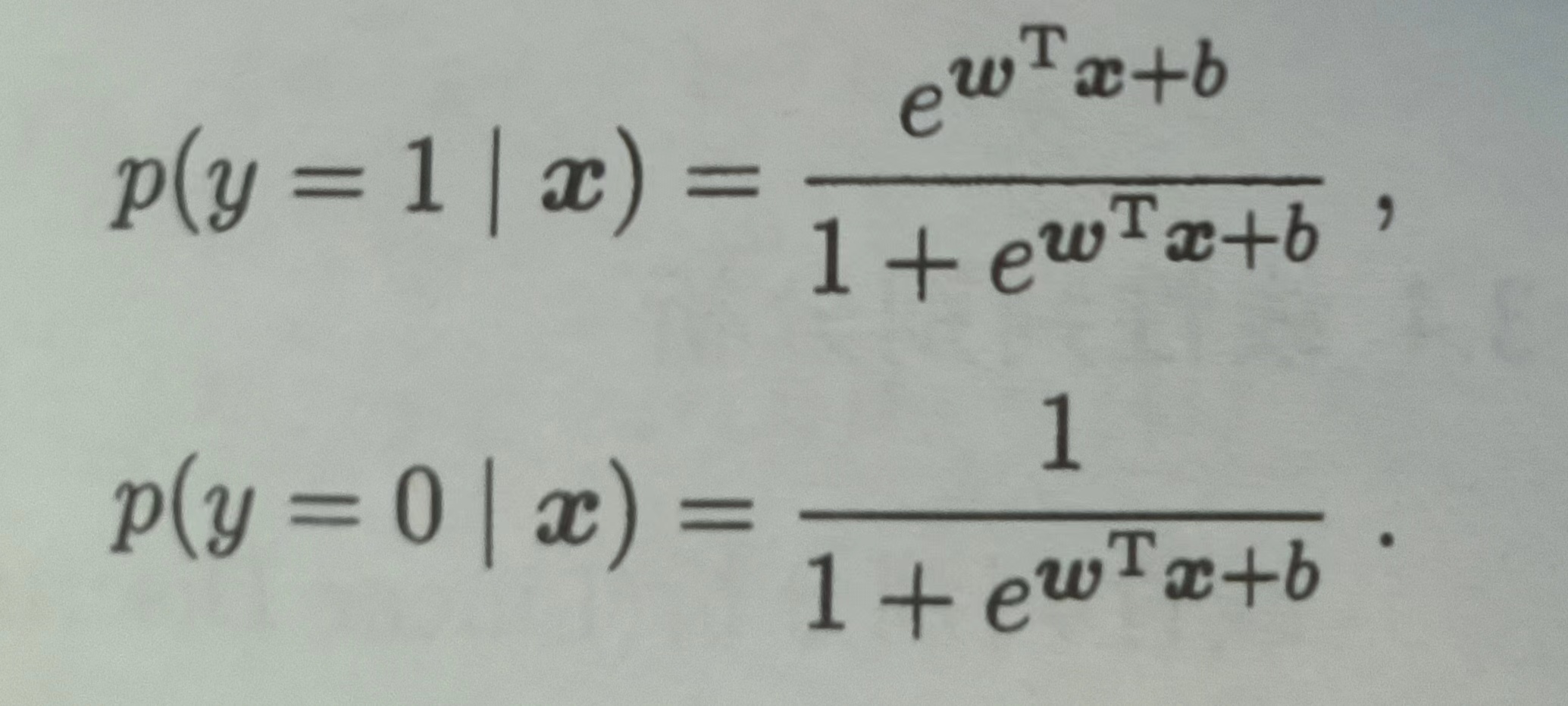
这个公式挺巧妙，但是我们手上并没有过去病人的得病概率，只有一组y。那么如何将这个公式与我们的真实标签y相联系起来，并求解这个公式中的参数呢？对于这种形式的回归，我们通常使用极大似然估计去求解，令每个样本属于其真实标记的概率越大越好。什么意思呢，当一个真实值y=1时，我们希望上面的结果尽可能大，当y=0时，我们希望下面的结果尽可能大。我们可以把这两个式子写成一个通项：

\[p（y_{i}|x_{i};\omega,b）= y_{i}*p_{1}(x_{i}) + (1-y_{i})*p_{0}(x_{i}) \]

这里的\(p_{1}\)和\(p_{0}\) 分别为上面两个式子的简写。
通过极大似然估计，我们可以得到“最有可能产生我们手上这组样本的参数”，我们认为这是对真实参数的一个良好估计，可以用来构建我们的模型。极大似然估计的方法属于是概率统计中比较巧妙但是基础的内容（概率统计的思想总是很巧妙），这里就不作过多介绍了。