矩阵求导（二）

前面已经介绍了标量对向量和矩阵的求导以及向量和矩阵对标量的求导，现在介绍一下向量和向量之间的求导规则。

• 向量对向量求导

不管被求导的向量是行向量还是列向量，我们求导的步骤都是统一的，只要选择了分母布局，其求导结果都是一个与分母同行数的矩阵，而列数则等于分子向量的维数。具体的求导过程如下：先将分子向量 f(\(\vec{y}\)) 沿纵向复制m份，每份分别对向量 \(\vec{y}\) 的分量 \({y}_1\) 至 \({y}_m\) 求偏导，再按照向量对标量的求导法则进行运算。最后的结果，等于一个m*n的矩阵。

• 常用的公式

矩阵对向量的求导不在本文的讨论范围之内，但是我们有一些常用公式可以使用。

• 下图的①是一个常用公式，他为我们提供了矩阵与向量的乘积对向量的导数。当A为一个向量时，公式同样成立，但是由于我们通常默认向量的形式为列向量，因此常用 \({{A}}^{T}\) \(\vec{y}\) 来表示两个向量的点积。此时，按照分母布局结果应当是列向量，也就是A。这个推理过程非常简单，只需要把\({{A}}^{T}\) \(\vec{y}\) 展开，就可以得到\(\sum {a}_i {y}_i\)，而这个标量对向量 \(\vec{y}\)的求导就是每个分量 \({y}_i\) 前面的系数 \({a}_i\) （只有这一项含有\({y}_i\) ）。
• 另一个常用的公式是公式②。一个二次型对向量的求导，本质是一个标量对向量的求导，只不过这个标量较为特别，可以很有规律地写成 \(\sum_{1}^{n}\sum_{1}^{n}{a}_{ij}{x}_i{x}_j\) 的形式。由于 \({{X}}^{T}\) 与X只是一个转置的关系，他们其实含有相同的元素值，所以这个算子可以对X进行完美地求导（只需要将最后一个向量按照每个分量左右两部分拆开，改写为为两个向量之和即可），结果正好是图上的形式。当A为一个对称阵时（通常情况下就是如此），答案会进一步简化为2AX.

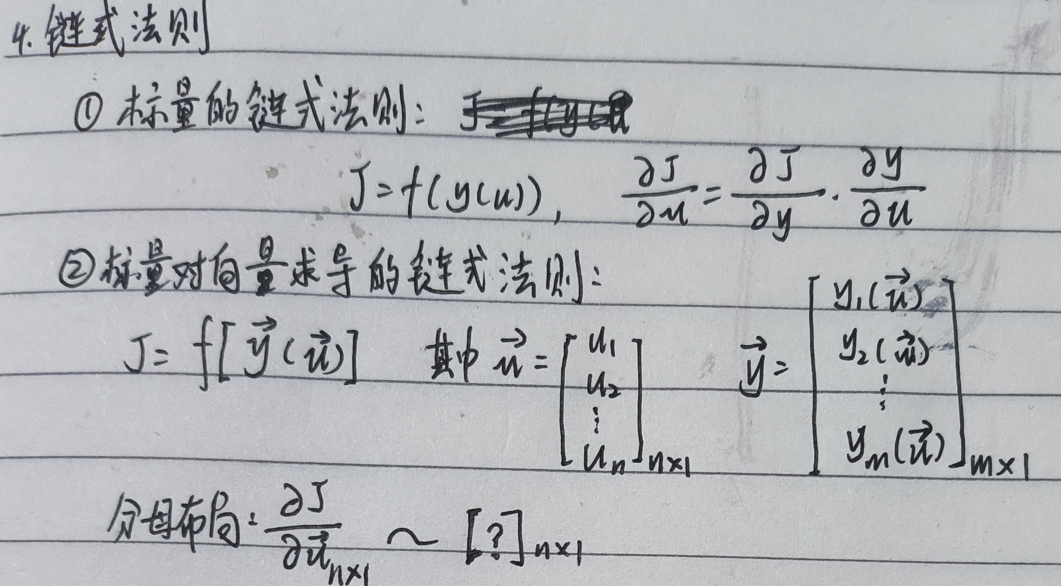
• 链式法则

向量求导的链式法则与标量的类似，由于我们现在使用分母布局，求导结果的形状是确定的。如果我们仅仅沿用标量的法则，则会出现形状无法对应的情况，此时我们想到标量的链式法则符合交换率，因此直接在向量求导中从右向左进行链式求导，就得到了想要的结果。