随笔分类 - 机器学习
Machine Learning,相对宽泛的主题
摘要：贝叶斯算法基本原理 在机器学习中主要用于分类，已知样本X， 1. 首先计算$P(X|C_i)$,得出Ci类别包含样本X的先验概率； 2. 然后根据贝叶斯定理求后验概率$P(C_i|X)$,得到X属于Ci类别的后验概率； 3. 最后根据最大后验概率判断所属类别。 朴素贝叶斯分类 朴素的含义 朴素地假设
阅读全文
摘要：逻辑回归从线性回归引申而来，对回归的结果进行 logistic 函数运算，将范围限制在[0,1]区间，并更改损失函数为二值交叉熵损失，使其可用于2分类问题(通过得到的概率值与阈值比较进行分类)。逻辑回归要求输入的标签数据是01分布(伯努利分布)，而线性回归则是对任意连续值的回归。出世：由统计学家 D
阅读全文
摘要：SpaceNet 数据集 "SpaceNet" 是DigitalGlobe商业卫星公司提供的遥感图像集合,包含一些标记信息可用作机器学习研究. SpaceNet Challenge主页: https://spacenetchallenge.github.io/ 数据集下载命令: https://gi
阅读全文
摘要：线性回归 用$X=(x_1, x_2, ...,x_n)T \in \mathbb{R}{n\times p}$表示数据，用$y=(y_1, y_2, ...,y_n)T \in \mathbb{R}{n}$表示标签。对于一个样本$x_i$，它的输出值是其特征的线性组合： \[ \begin{equ
阅读全文
摘要：BING 论文《BING: Binarized Normed Gradients for Objectness Estimation at 300fps》 南开大学媒体计算实验室,CVPR2014 http://mmcheng.net/bing/comment page 9/ 论文翻译:http:/
阅读全文
摘要：点到判决面的距离 点$x_0$到决策面$g(x)= w^Tx+w_0$的距离：$r={g(x)\over \|w\|}$ 广义线性判别函数 因任何非线性函数都可以通过级数展开转化为多项式函数（逼近），所以任何非线性判别函数都可以转化为广义线性判别函数。 Fisher LDA(线性判别分析) Fish
阅读全文
摘要：支持向量机就是使用了核函数的软间隔线性分类法，SVM可用于分类、回归和异常值检测（聚类）任务。“机”在机器学习领域通常是指算法,支持向量是指能够影响决策的变量。 示意图如下（绿线为分类平面，红色和蓝色的点为支持向量）： SVM原理 由逻辑回归引入[^course] 逻辑回归是从特征中学习出一个二分类
阅读全文
摘要：明氏距离(Minkowski Distance) $$ d(x,y)=(\sum_{k=1}^n|x_k y_k|^s)^{1\over s} $$ s越大,某一维上的较大差异对最终差值的影响也越大. s=1, 曼哈顿距离 s=2, 欧式距离 s=∞,上确界距离(Supermum Distance)
阅读全文
摘要：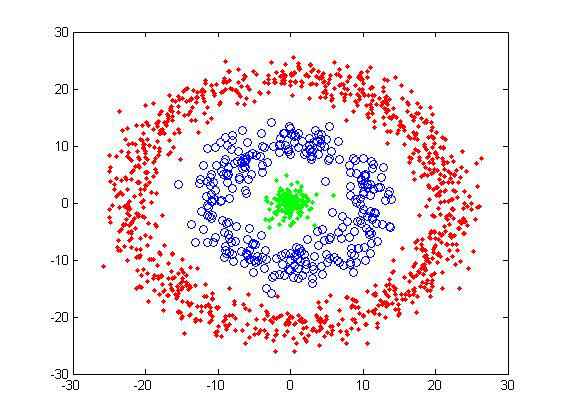
本篇内容包括划分聚类方法中的k-means、k-means++，基于密度的DBSCAN以及层次聚类等聚类方法。
阅读全文
本篇内容包括划分聚类方法中的k-means、k-means++，基于密度的DBSCAN以及层次聚类等聚类方法。
阅读全文
摘要：目录 "PCA思想" "问题形式化表述" "PCA之协方差矩阵" "协方差定义" "矩阵 特征值" "PCA运算步骤" "PCA理论解释" "最大方差理论" "性质" "参数k的选取" "数据重建" "主观理解" "应用" "代码示例" PCA思想 PCA主要用于数据降维,是一种无监督学习方法。主成
阅读全文
摘要：监督学习中通常通过对损失函数最优化（最小化）来学习模型。 本文介绍了几种损失函数和正则化项以及正则化对模型的影响。 损失函数 损失函数度量模型一次预测的好坏，风险函数度量平均意义下模型预测的好坏。 模型的输入输出是随机变量(X,Y)遵循联合分布P(X,Y),损失函数的期望是： \[ R_{exp}(
阅读全文
浙公网安备 33010602011771号
