逻辑回归(logistic regression)

逻辑回归从线性回归引申而来，对回归的结果进行 logistic 函数运算，将范围限制在[0,1]区间，并更改损失函数为二值交叉熵损失，使其可用于2分类问题(通过得到的概率值与阈值比较进行分类)。逻辑回归要求输入的标签数据是01分布(伯努利分布)，而线性回归则是对任意连续值的回归。出世：由统计学家 David Cox 在 1958 年提出。

从对数几率引入

一个事件发生的概率与不发生的概率的比值称为几率。对数几率(log odds)或称logit函数定义为：\(logit(p)=\log {p\over 1-p} \in \mathbb R\). 其中 \(p\) 为事件发生的概率。

我们希望得到一个模型使得样本被划分为正类的对数几率是特征 \(x\) 的线性组合，即\(\log{P(Y=1|x)\over P(Y=0|x)}=w\cdot x\)。并且当 \(w\cdot x \to +\infty\) 时 \(P(Y=1)\to 1\).

\[\begin{align} \log{P(Y=1|x)\over P(Y=0|x)} =& \log{P(Y=1|x)\over 1-P(Y=1|x)}=wx \\ \Longrightarrow & {P(Y=1|x)\over 1-P(Y=1|x)}=e^{wx} \\ \Rightarrow P(Y=1|x)=& {e^{wx} \over 1+e^{wx}} = {1\over 1+e^{-wx}} \end{align} \]

因此二项逻辑回归模型定义为:

\[\begin{align} P(Y=1|x)=& {e^{w\cdot x}\over 1+e^{w\cdot x}}={1\over 1+e^{-wx}} \\ P(Y=0|x)=& 1-P(Y=1|x) \end{align} \]

可以看出逻辑回归正是对输入进行线性组合后应用 sigmoid 函数。此外，logit 对数几率函数与 logistic 函数互为反函数。

值的注意的是 sigmoid 是 logistic 分布的一种特例。

logistic 分布^[1]

变量 \(X\) 具有 logistic 分布是指 \(X\) 具有以下分布函数 F(x) 和密度函数 f(x) :

\[\begin{align} F(x)&=P(X\le x)={1\over 1+e^{-(x-\mu)/\gamma}} \\ f(x)&=F'(x)=\dfrac{e^{-(x-\mu)/\gamma}}{\gamma(1+e^{-(x-\mu)/\gamma})^2} \end{align} \]

式子中,\(\mu\)是位置参数,\(\gamma>0\)是形状参数.
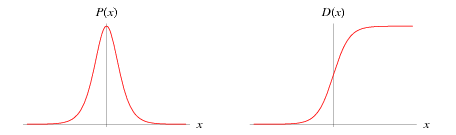
logistic 分布函数D(x)是一条S型曲线,概率密度函数P(x)是类似正态分布的钟型曲线.图示如下^[2]

模型参数估计

可以应用极大似然估计法估计模型参数:
设\(P(Y=1|x)=\pi(x),P(Y=0|x)=1-\pi(x)\)
似然函数为:

\[\Pi_{i=1}^N[\pi(x_i)]^{y_i} [1-\pi(x_i)]^{1-y_i} \]

对数似然函数为:

\[\begin{align} L(w)&=\log \Pi_{i=1}^N[\pi(x_i)]^{y_i} [1-\pi(x_i)]^{1-y_i} \\ &=\sum_{i=1}^N[y_i\log\pi(x_i)+(1-y_i)\log(1-\pi(x_i))] \end{align} \]

对L(w)求极大值,得到w的估计值.而我们实际中求-L(w)的极小值,即二值交叉熵损失(binary cross entropy).
二项逻辑回归的参数估计法可以推广到多项逻辑回归,即softmax.

损失函数

如果用平方误差（MSE）作为逻辑回归的损失函数,那么函数曲线将是跳跃式的,非凸的(non-convex),原因是logistic函数将数据范围限制在[0,1]区间,而真实标签值非0即1.最小化 MSE 损失容易陷入局部极小点.逻辑回归损失是如下的分情况的凸函数(单个x与y的损失):

\[\text{Cost}(h_\theta(x),y)=\begin{cases} -\log(h_\theta(x)) && \text{, $y=1$} \\ -\log(1-h_\theta(x)) && \text{, $y=0$} \end{cases} \]

符合直觉和逻辑.累计损失函数可以转化为如下(同时加上了正则项):

\[J(\theta)=[-{1\over m}\sum_{i=1}^m\big(y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log (1-h_\theta(x^{(i)}))\big)]+{\lambda \over 2m}\sum_{j=1}^n\theta_j^2 \]

可以看出, \(J(\theta)\) 与极大似然估计法所得的对数似然函数一致. 其中参数 \(\theta\) 同线性回归一样，用来对特征线性求和，可以使用梯度下降或者牛顿法来求解. 但逻辑回归最终要经过sigmoid函数得到输出：\(h_{\theta}(x)=g(\theta^{T}x)\)

\[g(z)={1\over 1+e^{-z}} \tag{sigmoid} \]

损失对\(\theta\)的偏导数为

\[\frac{\partial}{\partial\theta_{j}}J(\theta) ={1\over m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \]

偏导数推导也比较简单, 参考公式推导. 梯度下降公式为:

\[\theta_j := \theta_j-\alpha{1\over m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \]

在使用sigmoid激活函数时，MSE 损失得的W、b的梯度包含σ′(z)，因此存在反向传播收敛速度慢的问题，而交叉熵损失的梯度不包含σ′(z)。通常情况下，在使用sigmoid激活函数时，利用交叉熵损失函数肯定比均方差损失函数效果更好。

vs 回归模型

逻辑回归和线性回归都可看做广义的线性回归。逻辑回归仅比线性回归多了sigmoid函数非线性映射。
线性回归在整个实数域内敏感度一致,而逻辑回归将结果压缩到[0,1]以内,在远离0点的位置不敏感,可以更好地拟合数据。
当然,逻辑回归是用于分类,线性回归用于回归。

为什么LR模型的损失函数是交叉熵,而线性回归模型的损失函数却是最小二乘呢？能否随意确定一个损失函数作为目标呢？

模型的损失函数由各自的响应变量y的概率分布决定，对于线性回归模型，其输出是连续值，所以我们对于该问题假设y服从正态分布；相对的，LR模型一般用来解决二分类问题，所以其输出是0/1，故而我们假设其输出服从伯努利分布；而进一步地，两者的损失函数都是通过极大似然估计推导的来的，所以模型的损失函数并非随意确定。^[3]

分类模型与回归模型之间有种种联系,比如 SVM 模型可以看作逻辑回归加L2正则项, 并使用了不同的损失函数. 预测结果的概率值可以通过 Platt's scaling 得到.

为什么不使用回归模型来做分类?^[4]
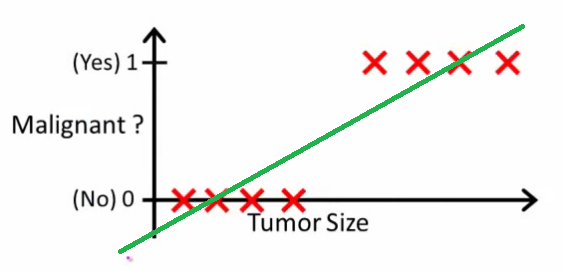
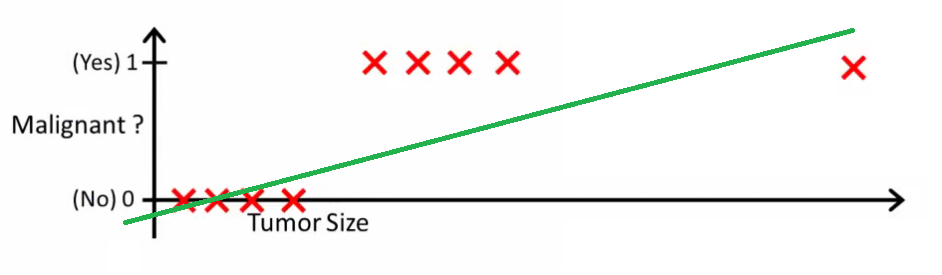
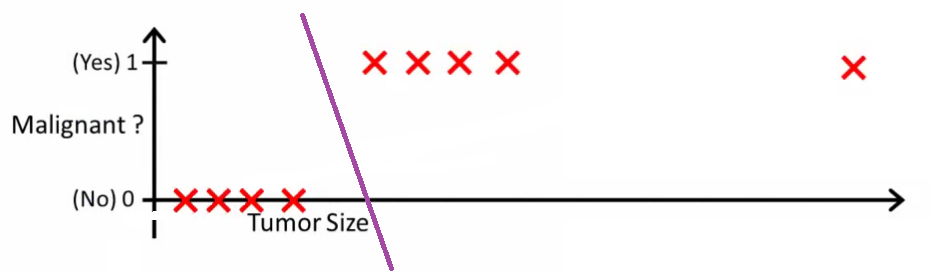
比如对于二分类, 做一个线性回归模型,然后通过预测值与阈值的比较进行分类.
这是一种不好的做法, 因为阈值不好确定, 随着数据集的变动, 阈值也需要有较大变化.

首先明确逻辑回归(分类)与线性回归的区别: 线性回归是去拟合数据的连续值属性, 而逻辑回归是预测属于类别的概率,因此逻辑回归是一个回归问题. 逻辑回归通过概率输出与阈值(如0.5)的比较确定最终分类,也因此常被看作分类问题.

vs 最大熵模型

最大熵模型: 在约束条件下最大化条件概率分布的条件熵，约束条件是特征函数相对联合分布的期望等于特征函数相对于模型和条件分布的期望。通过求解这个约束最优化问题(转为拉格朗日对偶问题^[1:1] ), 可以得到在给定输入变量 x 时，输出变量 y 的条件分布：

\[P(y | \mathbf{x}, \boldsymbol\theta) = \frac{ \exp\left( \boldsymbol\theta \cdot \mathbf{f}(\mathbf{x}, y) \right) }{ \sum_{\mathbf{y} \in \textit{Dom}(y)} { \exp\left( \boldsymbol\theta \cdot \mathbf{f}(\mathbf{x}, y) \right) } } \]

此处\(\textit{Dom}(y)\)是y所有可能取值的集合。我们可以看出这正是softmax的公式形式.
当y的类别为2类时上式与逻辑回归之间的显著差别在于特征函数.
取

\[f (x,y) = \begin{cases} g(x) & y=y_1 \\ 0 & y=y_0 \end{cases} \]

即仅在y=y1时抽取 x的特征。在y=y0时不抽任何特征（直接返回全为 0 的特征向量）。^[5]

\[P(y|x) = \begin{cases} \sigma(\theta \cdot g(x)) & y=y_1 \\ 1-\sigma(\theta \cdot g(x)) & y=y_0 \end{cases} \]

可以得到与逻辑回归相同的表达式.

逻辑回归是最大熵模型的一个特殊例子(二类的情况).二项式分布的最大熵等价于二项式指数形式(sigmoid)的最大似然；
多项式分布的最大熵等价于多项式分布指数形式(softmax)的最大似然。^[6]

多值交叉熵(softmax)

令\(\pi(x)_u\)表示输入 x 得到的 y=u 的概率,

\[\pi(x)_u=\frac{e^{w_u\cdot x}}{\sum_{v=1}^k e^{w_v \cdot x}} \]

我们的目标是最大化\(\pi(x_i)_{y_i}\),最大熵模型的极大似然估计是:

\[L(w)=\prod_{i=1}^n \pi(x_i)_{y_i} \]

另外, 再说说多项式分布:
假设类别\(y\in \{1,...,k\}\),每个类别统计的样本个数分别为\(n_1,n_2,\cdots,n_k\),且\(\sum_{i=1}^k n_i=n\).假设样本服从多项式分布且相互独立,那么概率密度函数为

\[P(D|\theta)={n!\over n_1!\cdot n_2!\cdots n_k!}\prod_{i=1}^k p_i^{n_i} \]

取对数得:

\[\log P(D|\theta)=\log n!-\log n_1!\cdot n_2!\cdots n_k!+\sum_{i=1}^k n_i\log p_i \]

前边的log项与参数\(\theta\)无关,因此最大化似然函数等价于最小化:

\[-\sum_{i=1}^k n_i\log p_i \]

vs 感知机

同：原始模型均为二分类，训练方法都是使用梯度下降法。
异：感知机是符号函数sign，输出为类别1/-1；LR是sigmoid输出为概率值。

vs Linear SVM

• Linear SVM和LR都是线性分类器
• Linear SVM不直接依赖数据分布，分类平面不受一类点影响；LR则受所有数据点的影响，如果不同类别数据严重不平衡需要先对数据做balancing。
• Linear SVM依赖数据表达的距离测度，所以需要对数据先做normalization(归一化)；LR不受其影响
• Linear SVM依赖penalty的系数，实验中需要做validation
• Linear SVM和LR的performance都会收到outlier的影响，其敏感程度而言，谁更好很难下明确结论。

正则项

• L2 解决过拟合
• L1解决数据稀疏性问题.，比如Google13年出的预估方法－FTRL模型，虽然是在线学习算法，但主要是为了解决预估时的稀疏性问题。
• 超大规模稀疏LR模型学习问题，LR模型自身是做不到的。这个时候需要我们为它选择一个学习算法和分布式系统。在分布式环境下，约束优化求解理想方案之一－ADMM算法（交叉方向乘子法），可用于求解形式为”loss function + 正则项”目标函数极值问题。

L1和L2正则先验分别服从什么分布

从信息论的角度看，向系统加入了正确先验这个信息，肯定会提高系统的性能。
L1是拉普拉斯分布，L2是高斯分布。

拉普拉斯分布:

\[f(x|\mu,b)={1\over 2b}e^{-{|x-\mu|\over b}} \]

模型的优势

逻辑回归相比其它更复杂的模型的优势：

• LR 能以概率的形式输出结果,而非只是 0,1 判定; 而其它模型如 SVM 难以用概率表示,虽然存在多种概率校准方法, 但仍不能与LR的概率形式相比；
• LR 的可解释性强,可控度高；
• 训练快,feature engineering 之后效果好；
• 因为结果是概率,可以做 ranking model；
• 添加 feature 很简单。

缺点

• 容易欠拟合，一般准确度不太高
• 只能处理两分类问题. (可以应用多个逻辑回归实现多分类,类似SVM的方式; 另外对于父子类别同时分类的情况,使用逻辑回归要比Softmax等方式效果好)

在现实中很多推荐系统都是拿 LR 做基础版本的,其作用不容小觑.

常见应用场景

• 预估问题场景（如推荐、广告系统中的点击率预估，转化率预估等）
• 分类场景（如用户画像中的标签预测，判断内容是否具有商业价值，判断点击作弊等.

为什么要对特征进行离散化

在工业界，很少直接将连续值作为逻辑回归模型的特征输入，而是将连续特征离散化为一系列0、1特征(one-hot编码)交给逻辑回归模型，这样做的优势有以下几点：^[7]

1. 离散特征的增加和减少都很容易，易于模型的快速迭代；
2. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
3. 离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
4. 逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；
5. 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
6. 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；

李沐曾经说过：模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型，也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。通常来说，前者容易，而且可以n个人一起并行做，有成功经验；后者目前看很赞，能走多远还须拭目以待。

逻辑回归并行化

对于逻辑回归，有些可以并行化，但是有些是很难并行化的（或者说很难无损的并行化）。比如FTRL这类在线算法较难并行。一般的逻辑回归计算简单，存储资源占用低，很容易并行。

优化方式: 一阶的 Gradient Descent (GD-LR), 二阶的L-BFGS, 以及ADMM.

开源的并行化代码: 在分布式机器学习框架Angel中分别提供了利用Gradient Descent、ADMM两种优化方法计算的LR算法。

Gradient Descent (GD-LR)

逻辑回归的cost function对参数的偏导数是：

\[\frac{\partial J}{\partial \theta}=\frac{1}{M} {\sum_{i=1}^{M}{(h_\theta(x^{(i)})-y^{(i)}})\times x^{(i)}} \]

参数更新需要所有样本的损失的平均值,而每个样本的损失计算仅与该样本有关, 因此很容易实现并行化. 我们能够很容易地想到MapReduce的思想, Map划分样本,Reduce收集样本梯度. 但是MapReduce存在需要文件IO,Reduce单点问题扩展性差等问题.而现代的深度学习框架多基于MPI实现并行计算. 另外,在计算总体的损失更新参数后需要分发给各计算节点, 这通常采用参数服务器的设计方式.

如果数据量大到集群都撑不下时,我们一般也并不需要每次迭代更新参数时计算所有样本,而是选取一部分进行Mini-batch gradient Descent(或称SGD).

仅按样本并行

将样本划分为 B 块(随机不重复), 每块的样本集合记作\(S_k\), 则有：

\[\frac{\partial J}{\partial \theta}= \frac{1}{M} \sum^{B}_{k=1}{\sum_{i \in S_k}{(h_\theta(x^{(i)})-y^{(i)}})\times x^{(i)}} \]

这样就可以实现按样本划分的并行化加速了，就是这么简单。^[8]

特征并行^[9]

如果特征维数比较多,如广告系统中的特征维度高达上亿,这种情况下内存也不够用, 可以对特征进行分组, 拆分到不同的机器进行计算. 这样将MxN的训练样本划分到mxn的网格集群中进行并行计算,每台机器计算量为(M/m)x(N/n).
那么这里需要考虑的问题是特征能否并行? 该怎样并行?
每个样本的梯度是: \(G_i=(h_\theta(x^{(i)})-y^{(i)})\times x^{(i)}\)
其中\(h_\theta(x^{(i)})-y^{(i)}=\sigma(\theta^{T}x^{(i)})-y^{(i)}\) 是标量, 而 \(x^{(i)}\) 是向量. \(\sigma(\theta^{T}x^{(i)})\) 需要计算样本 \(x^{(i)}\) 的所有特征分量与参数的乘积,求和之后执行sigmoid运算. 因此在集群网格中第r行的计算节点计算相应分量(第c列对应的特征向量)的 \(\theta_c^{T}x^{(r,c)}\) 之后得到 \(\sigma(\theta^{T}x^{(i)})\) 标量, 然后再回传到第r行的每一个计算节点, 进而计算\(G_{r,c}=(h_\theta(x^{(r,c)})-y^{(r)})\times x^{(r,c)}\).
现在只需对每一列分别求平均值即可得到用来更新参数的梯度向量 \(G_\theta\).

ADMM^[10][11]

用 ADMM 求解LogisticRegression的优化方法称作ADMM_LR。ADMM算法是一种求解约束问题的最优化方法，它适用广泛。相比于SGD，ADMM在精度要求不高的情况下，在少数迭代轮数时就达到一个合理的精度，但是收敛到很精确的解则需要很多次迭代。
ADMM算法结合了对偶分解法(Dual Decomposition)和增广拉格朗日乘子法(Augmented Lagrangians and the Method of Multipliers)的优势，它可以在满足较弱收敛条件的情况下，分解目标函数，交替地更新变量，直至算法收敛。
在ADMM在每一步的优化过程中，可以与牛顿法等高精度算法相结合进行求解。

在Angel的实现上，采用样本并行的方式, 每个计算节点上使用L-BFGS, 使用参数服务器汇总计算整体的参数.

---

1. 《统计学习方法》（李航，清华大学出版社） ↩︎ ↩︎

2. http://mathworld.wolfram.com/LogisticDistribution.html ↩︎

3. http://izhaoyi.top/2017/07/08/lr/ ↩︎

4. https://stats.stackexchange.com/questions/22381/why-not-approach-classification-through-regression ↩︎

5. https://www.zhihu.com/question/24094554 ↩︎

6. Logistic Regression 的前世今生（理论篇） https://blog.csdn.net/cyh_24/article/details/50359055 ↩︎

7. http://wangxin123.com/2017/10/19/机器学习（一）：回归算法/ ↩︎

8. Logistic回归的CPU并行化及其 Batch Gradient Ascent 的实现 https://zhuanlan.zhihu.com/p/20511129 ↩︎

9. 并行逻辑回归 http://blog.sina.com.cn/s/blog_6cb8e53d0101oetv.html ↩︎

10. Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine Learning, 2011, 3(1): 1-122. ↩︎

11. https://github.com/Tencent/angel/blob/master/docs/algo/admm_lr_on_angel.md ↩︎