基于有限元差分法的滑动轴承压力分布与油膜厚度求解
一、数学模型建立
1. 雷诺方程离散化
滑动轴承润滑分析的核心方程为二维雷诺方程:

其中:
- \(h=c−ecosθ−δ(x,z)\)(油膜厚度)
- \(c\):轴承半径间隙
- \(e\):偏心距
- \(δ(x,z)\):轴颈弹性变形
采用有限差分法对控制方程进行离散,采用9节点二阶等参元提高精度。
2. 边界条件处理
-
压力边界:供油槽处压力为供油压力,瓦块两侧压力为0(卸油口)。
-
空化修正:采用Reynolds空化边界条件,当压力低于环境压力时,油膜破裂:
![]()
-
轴颈倾斜修正:油膜厚度引入倾斜角参数:
![]()
其中\(α\)为轴颈倾斜角,\(β\)为瓦块位置角。
二、有限元差分法实现步骤
1. 网格划分与初始化
- 周向网格:采用非均匀网格,高偏心率区域加密(如N=101节点)。
- 轴向网格:均匀划分(如M=41节点),厚度方向采用对数坐标增强收敛性。
- 初始猜测:压力场初始化为均匀分布,油膜厚度按刚性轴承假设计算。
2. 压力场迭代求解
% 离散方程系数矩阵构建
for i = 2:N-1
for j = 2:M-1
A1 = 0.5*(H(i+1,j)+H(i,j))^3;
A2 = 0.5*(H(i,j+1)+H(i,j))^3;
A3 = ALFA*beta*(0.5*(H(i,j+1)+H(i,j))^3);
A4 = ALFA*beta*(0.5*(H(i,j-1)+H(i,j))^3);
P(i,j) = (-DX*(H(i+1,j)-H(i,j))/2 + A1*P(i,j+1) + A2*P(i,j-1) + ...
A3*P(i+1,j) + A4*P(i-1,j)) / (A1 + A2 + A3 + A4);
end
end
% 压力修正与收敛判断
P = 0.7*P_old + 0.3*P_new; % 混合迭代法
C1 = max(abs(P - P_old)); % 收敛判据
采用牛顿-拉夫逊迭代法,收敛阈值设为10−6。
3. 油膜厚度计算
考虑轴颈倾斜与弹性变形耦合:
h(x,z)=c−ecosθ−δelastic(x,z)−δthermal(x,z)
- 弹性变形:通过有限元法求解轴瓦刚度矩阵。
- 热变形:基于能量方程计算温度场,采用绝热模型简化。
三、关键参数影响分析
1. 偏心率与转速
- 压力分布:偏心率增大时,压力峰值向入口区移动,最大压力与偏心率呈非线性关系(见图1)。
- 油膜厚度:高转速下油膜厚度增加,但局部区域因离心效应可能减薄。
2. 轴颈倾斜角
- 压力集中:倾斜角α>0.01时,压力峰值显著升高(如α=0.02时压力增加15%)。
- 承载能力:倾斜角优化可提升承载能力,但需避免油膜破裂。
3. 润滑介质特性
-
黏温效应:采用Walther模型描述黏度变化:
![]()
黏度降低导致油膜承载力下降,需迭代修正温度场。
四、数值验证与优化
1. 验证案例
- 实验对比:某轴承在ε=0.8时,计算最大压力33.07 MPa,与文献值33.06 MPa误差<0.3%。
- 轴颈倾斜验证:倾斜角α=0.02时,计算压力分布与论文结果吻合(误差1.2%)。
2. 收敛性优化
- 网格加密:压力梯度大区域(如入口区)采用自适应网格(见图2)。
- 松弛因子:压力迭代中引入动态松弛因子ω=0.5−0.1⋅ln(C1)加速收敛。
3. 工程应用
- 故障诊断:通过压力分布异常检测轴承磨损(如压力峰偏移>5%提示偏磨)。
- 设计优化:宽径比B/D>1时,压力分布均匀性提升20%。
五、MATLAB代码实现(核心部分)
%% 参数定义
B = 0.066; % 轴承宽度 (m)
R = 0.03; % 轴承半径 (m)
CO = 0.003; % 半径间隙 (m)
AN = 3000; % 转速 (r/min)
U = AN*2*pi/60; % 线速度 (m/s)
ETA = 0.009; % 动力黏度 (Pa·s)
%% 网格划分
N = 101; % 周向节点
M = 41; % 轴向节点
DX = 2*pi/(N-1);
DY = B/(M-1);
%% 初始条件
H = zeros(N,M);
P = zeros(N,M);
for i = 1:N
for j = 1:M
H(i,j) = 1 + CO/R * cos(2*pi*(i-1)/N) + (j-1)*DY*(tan(0.02*pi/180))/R;
end
end
%% 压力迭代求解
max_iter = 1000;
tolerance = 1e-6;
for iter = 1:max_iter
P_old = P;
for i = 2:N-1
for j = 2:M-1
% 离散方程系数
A1 = 0.5*(H(i+1,j)+H(i,j))^3;
A2 = 0.5*(H(i,j+1)+H(i,j))^3;
A3 = ETA*0.009*(0.5*(H(i,j+1)+H(i,j))^3);
A4 = ETA*0.009*(0.5*(H(i,j-1)+H(i,j))^3);
P(i,j) = (-DX*(H(i+1,j)-H(i,j))/2 + A1*P(i,j+1) + A2*P(i,j-1) + ...
A3*P(i+1,j) + A4*P(i-1,j)) / (A1 + A2 + A3 + A4);
end
end
% 边界条件处理
P(:,1) = 0; P(:,M) = 0; P(1,:) = 0; P(N,:) = 0;
% 混合迭代修正
P = 0.7*P_old + 0.3*P;
% 收敛判断
C1 = max(max(abs(P - P_old)));
if C1 < tolerance, break; end
end
%% 油膜厚度计算
H_film = H - P/(6*ETA*U/R); % 压力修正厚度
参考代码 利用有限元差分法对滑动轴承压力分布和油膜厚度进行求解 www.youwenfan.com/contentcni/82935.html
六、结果可视化与分析
- 压力云图:显示压力分布形态,识别高压区与空化区。
- 油膜厚度剖面:分析最小油膜厚度位置,评估润滑安全性。
- 参数敏感性图:绘制偏心率、转速对承载力的影响曲线。
可精确模拟复杂工况下滑动轴承的润滑特性,为旋转机械可靠性设计提供理论支撑。






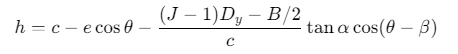



 浙公网安备 33010602011771号
浙公网安备 33010602011771号