洛谷 P1099 题解

洛谷 P1099 【NOIP 2007 提高组】 树网的核

题意简述

给定一棵 \(n\) 个结点的带边权无根树和一个正整数 \(s\)。在这棵树的任意直径上截取一段长度不超过 \(s\) 的路径 \(F\)，使离 \(F\) 最远的点到 \(F\) 的距离最小，求出这个距离。

思路

记 \(\delta(a, b)\) 为 \(a, b\) 之间的路径。

对于任意直径上一点 \(u\)，记 \(d'(u)\) 为 \(u\) 不经过直径上其他点所能到达的最远距离。

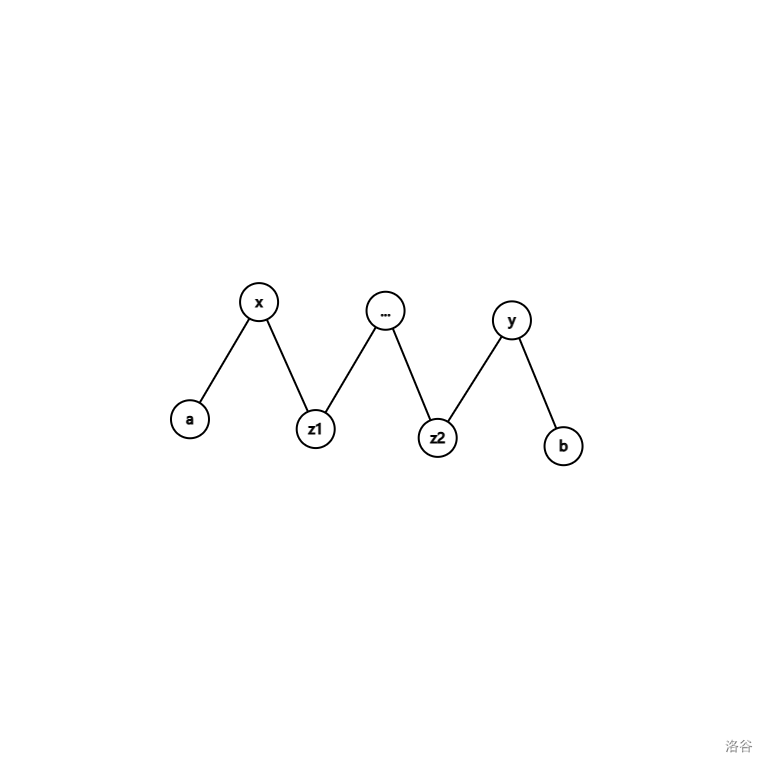
如图，不妨设一条直径为 \(\delta(a, b)\)，其中的一条路径 \(F = \delta(x, y)\) 满足 \(d(x, y) \le s\)。

引理： 对于直径 \(\delta(a, b)\) 上任意一点 \(u\)，总有 \(d'(u) \le d(a, u), d(b, u)\)。

证明：假设 \(d'(u) > d(a, u)\)，不妨设 \(u\) 不经过直径上其他点所能到达的最远的点是 \(a'\)（即 \(d'(u) = d(a', u)\)），则有 \(d(a', b) = d(a', u) + d(u, b) > d(a, u) + d(u, b) = d(a, b)\)，与 \(\delta(a, b)\) 是树的直径矛盾。\(d'(u) \le d(b, u)\) 同理。

由引理及 \(\operatorname{ECC}\) 的定义可得出以下性质：

1. \(z\) 对 \(\operatorname{ECC}(F)\) 的贡献是 \(d'(z)\)。

2. \(x\) 对 \(\operatorname{ECC}(F)\) 的贡献是 \(d(a, x)\)，\(y\) 对 \(\operatorname{ECC}(F)\) 的贡献是 \(d(b, y)\)​。

由以上二点可得对于 \(F = \delta(x, y)\) 有 \(\operatorname{ECC}(F) = \max\{d(a, x), d(b, y), \max\{d'(z)\} \}\)。

3. \(\operatorname{ECC}(F) \le \operatorname{ECC}(\delta(x, z_2)), \operatorname{ECC}(\delta(y, z_1))\)。

   证明：由上式得

   \[\begin{cases} \operatorname{ECC}(F) = \max\{d(a, x), d'(z_1), \cdots, d'(z_2), d(b, y) \}, \\ \operatorname{ECC}(\delta(x, z_2)) = \max\{d(a, x), d'(z_1), \cdots, d(b, z_2) \}, \\ \operatorname{ECC}(\delta(y, z_1)) = \max\{d(a, z_1), \cdots, d'(z_2), d(b, y) \}. \end{cases} \]

   由引理知 \(d'(z_1) \le d(a, z_1), d'(z_2) \le d(b, z_2)\)，又易证 \(d(a, x) < d(a, z_1), d(b, y) < d(b, z_2)\)，代入得证。

综上，由 1、2 我们得知对于 \(F = \delta(x, y)\) 如何计算 \(\operatorname{ECC}(F)\)；由 3 归纳得知仅当 \(d(x, y)\) 尽可能接近 \(s\) 时最优，满足单调性，这提示我们使用双指针。

使用两遍 DFS 找出一条直径 \(\delta(a, b)\)。指定 \(a\) 为根结点；在第二次 DFS 时记录每个结点的父节点，记为 \(fa\)；求出每个结点到 \(a\) 的距离，记为 \(dis\)。再使用一遍 DFS 求出直径上每个点的 \(d'\)。在这条直径上使用双指针枚举 \(x, y\) 确定 \(F\)；\(d(a, x)\) 和 \(d(b, y)\) 可以在尺取的过程中用 \(dis\) 递推得出，\(\max \{ d'(z) \}\) 可以用单调队列维护，由此求得 \(\operatorname{ECC}(F)\)。\(\min \{\operatorname{ECC}(F) \}\) 即为答案。

DFS、双指针、单调队列时间复杂度均为 \(O(n)\)，故总时间复杂度 \(O(n)\)。

考虑进一步简化。在尺取的过程中求出所有 \(F\) 的 \(\max\{d(a, x), d(b, y) \}\) 的最小值，记为 \(r\)；求出所有 \(d'\) 的最大值，记为 \(d'(t)\)。

设 \(F' = \delta(x', y')\) 是答案对应的区间。

• 若 \(r \ge d'(t)\)，则 \(\operatorname{ECC}(F') = \max\{d(a, x'), d(b, y' )\} = r\)。

• 若 \(r < d'(t)\)，则一定有 \(t\) 在 \(F'\) 上，即 \(x' \le t \le y'\)，此时 \(\operatorname{ECC}(F') = d'(t)\)。假设 \(t\) 不在 \(F'\) 上，不妨设 \(t < x'\)，由引理知 \(d'(t) \le d(a, t) < d(a, x’) \le \operatorname{ECC}(F')\)，一定不如 \(t\) 在 \(F'\) 上优。

所以最终答案为 \(\max \{r, d'(t) \}\)。

考察存在多条直径的情况。题面已经指出直径的中点重合，可以证明每条直径总有一段路径相交，去除直径“分岔”的部分关于这条路径对称，如果 \(F'\) 包含了直径分岔的结点 \(m\)，则 \(\operatorname{ECC}(F')\) 为 \(m\) 到 \(F'\) 末端的距离，因此选择任何一条直径都不影响结果。具体证明较为繁琐，这里略去。

代码

#include <iostream>
#include <vector>

struct Edge // 边
{
    int to, w; // 终点和边权
};

int far; // 用于求直径端点

int fa[305], dis[305];     // fa 为以 a 为根每个点的父节点, 为了省事 dis 和 d' 都用 dis[] 来存储
bool diameter[305];        // 是否在直径上
std::vector<Edge> mp[305]; // 存树

void dfs(int u, int f) // 为了省事, 求直径, dis, d' 全部放进了一个函数里
{
    fa[u] = f;
    if (dis[u] > dis[far])
        far = u; // 求直径的端点
    for (auto i : mp[u])
        if (i.to != f && !diameter[i.to]) // i.to != f 避免死循环, !diameter[i.to] 是 d' 的定义
        {
            dis[i.to] = dis[u] + i.w;
            dfs(i.to, u);
        }
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);

    int n, s, ans = 300000;
    int a, b; // 直径的端点

    std::cin >> n >> s;
    for (int i = 1; i < n; i++) // 建图
    {
        int u, v, w;
        std::cin >> u >> v >> w;
        mp[u].push_back({v, w});
        mp[v].push_back({u, w});
    }

    // 求直径
    dfs(1, 0);
    a = far;
    dis[a] = 0;
    dfs(a, 0);
    b = far;

    for (int x = b, y = b; x >= 1; x = fa[x]) // 双指针
    {
        while (dis[y] - dis[x] > s) // 性质 3, 仅当 d(x, y) 尽可能接近 s 时最优
            y = fa[y];
        ans = std::min(ans, std::max(dis[b] - dis[y], dis[x])); // 求所有 F 的 max{d(a, x), d(b, y)} 的最小值
    }

    for (int i = b; i >= 1; i = fa[i]) // 标记直径, 为求 d' 做准备
        diameter[i] = true;
    for (int i = b; i >= 1; i = fa[i]) // 求 d'
    {
        dis[i] = 0;
        dfs(i, fa[i]);
    }

    for (int i = 1; i <= n; i++) // 求 d'(t)
        ans = std::max(ans, dis[i]);

    std::cout << ans << "\n";

    return 0;
}