如何快速发明各种串串算法

串串的各种算法思想太巧妙了，并且串串题的数量比较少。

因此需要一种能够快速回忆起各种串串算法的小技巧。

算法按照发明难度排序。

你可能需要了解的：

\(\sum\) 表示字符集，通常为小写字母 \(\texttt{a}\sim \texttt{z}\)。\(|\sum |\) 表示字符集的大小，若字符集为全体小写字母时 \(|\sum|\) 为 \(26\)。

\(S[x\dots y]\) 表示 \(S\) 的第 \(x,x+1,\dots,y-1,y\) 个字符组成的字符串，是 \(S\) 的一个子串。本文中所有字符串均为 1-index。

什么是自动机？

1. 哈希

这个真没啥好说的吧，要说的话就两个点。

1. 将字符串视作 \(k\) 进制，并考虑其在 \(k\) 进制下每一位的权值。
2. 只有双哈希的正确性是有保证的。（生日悖论等）

2. Trie 树

用一个节点来表示某个串的前缀，对于两个串的公共前缀，尝试将它们合并到同一个节点。

发现合并完之后是一个树形结构。

每个节点维护一个大小为 \(|\sum|\) 的出边数组即可很方便的实现。

3. SA（后缀数组）

目标：求出 \(S\) 每个后缀的字典序在所有后缀中的排名。

先考虑如何将最基本的将 \(S\) 的所有后缀按照字典序排序。

如果只考虑每个后缀的第一个字符间的大小关系，显然可以直接排序。

如果要比较两个字符串的字典序，肯定是从前到后的比较。并且每次可以比较不止一位，只要知道两个字符串这若干位之间整体的大小关系即可。

考虑倍增长度，假设进行第 \(x\) 轮的之前我们已经知道各个后缀的前 \(2^{x-1}\) 的字符的字典序大小关系。

令 \(S_i\) 为 \(S[i\dots n]\)，也就是从 \(i\) 开始的后缀。这时候我们发现，\(S_i\) 和 \(S_j\) 的第 \(2^{x-1}+1\) 位到第 \(2^x\) 位之间的整体大小关系恰好等于 \(S_{i+2^x}\) 于 \(S_{j+2^x}\) 的前 \(2^{x-1}\) 位之间的整体大小关系。

因此可以将 \(S_i\) 的字典序视作一个二元组，第一元是 \(S_i\) 在上一轮之中的字典序，第二元是 \(S_{i+2^x}\) 在上一轮之中的字典序。直接对这一堆二元组进行排序即可得到各个后缀比较前 \(2^x\) 字符得到的大小关系。

直接实现是 \(O(n\log ^2 n)\) 的，由于值域很小（为 \(\max(|\sum|,n)\)），所以可以使用基数排序优化到 \(O(n\log n)\)。线性 SA 一般是比较 useless 的，所以这里不作研究。

这里继续研究如何如何具体实现基数排序，因为这个可能比较容易忘。

首先对一元组基数排序只需要开个桶，把元素在桶里添加贡献，把桶求前缀和然后倒着扫一遍元素就可以求出排名了。倒着扫是因为这样不会改变相同元素一开始的位置关系。

接着考虑如何对二元组进行基数排序。肯定先对第二元做一次基数排序，这样在第一元的基数排序的最后一边扫描就可以按照第二元从大到小进行扫描。

具体找位置的代码结构大概是这样的：

按照第二元顺序从大到小枚举，这个元素的实际排名是第一元的桶中小于等于这个元素第一元大小的元素的个数。

还有一个 \(height\) 数组，后面再补。

4. ACAM

目标：求出一个自动机，满足：

1. 每个字符串的所有前缀都恰好对应自动机上的一个节点（包括空串）。
2. 每个节点均有 \(|\sum|\) 条出边，一条出边上有一个字符 \(c\)。一个节点的所有出边上的字符互不相同。
3. 设节点 \(x\) 所对应的字符串为 \(T_x\)。若 \(u\) 走出边 \(c\) 后到达 \(v\)，则 \(v\) 满足以下条件：
   • \(T_v\) 为 \(T_u+c\)（字符串拼接）的后缀。
   • \(v\) 是所有满足条件的节点中 \(|T_v|\) 最大的。

首先考虑建出 Trie，然后对其进行一些操作。

现在对于一个节点 \(u\) 的字符串已经知道其所有前缀在 Trie 树上的哪些位置（不断跳 Trie 树父亲即可从长到短遍历所有前缀）。

目标是找到一种方式能够快速表示 \(u\) 的所有后缀在树上的位置吗，某个后缀没有就不表示。

类比遍历前缀的方法，由于 \(u\) 的最长存在于 Trie 树中的后缀是可以确定的，并且后缀之间是包含关系，所以用一个指针 \(fail_u\) 表示 \(u\) 在 Trie 树中的最长真后缀。

考虑 \(u\) 的所有后缀与其在 Trie 树上父亲节点（\(fa_u\)）的所有后缀的关系。

发现 \(u\) 的所有后缀（包括 \(u\)）一定可以通过 \(fa_u\) 的某个后缀走 Trie 树上的一条边得到。

因此考虑从 \(fa_u\) 的后缀节点集合得到 \(u\) 的后缀节点集合。

具体来说，维护的方式如下：

• 按照节点深度从小到大 bfs，因为 \(u\) 的真后缀的长度一定小于 \(u\) 的长度。
• 令 \(tr_{u,c}\) 的含义从 Trie 树上的边变为 节点 \(u\) 及其所有后缀 走出边 \(c\) 后能到达的长度最长的节点。
• 根据 Trie 树上出边 \(c\) 是否存在分讨如何更新 \(fail\) 及 \(tr\)。

5. KMP

目标：求出 \(S\) 每个前缀的所有 Border。

你说不知道啥是 Border？\(T\) 是 \(S\) 的 Border 当且仅当 \(T\) 是 \(S\) 的前缀且 \(T\) 是 \(S\) 的后缀且 \(T\neq S\)。

Border 之间是有包含关系的，并且可以通过这个知道如果 \(S\) 有两个 Border \(T_1\) 和 \(T_2\)（\(T_1\) 比 \(T_2\) 长），那么 \(T_2\) 也是 \(T_1\) 的 Border。

证明

考虑 \(T_1\) 是 \(S\) 的前缀、\(T_2\) 是 \(T_1\) 的前缀；\(T_1\) 是 \(S\) 的后缀、\(T_2\) 是 \(T_1\) 的后缀，所以 \(T_2\) 既是 \(T_1\) 的前缀又是 \(T_1\) 的后缀，并且 \(T_2\) 比 \(T_1\) 短，所以 \(T_2\) 是 \(T_1\) 的 Border。

所以对于一个前缀 \(S[1\dots i]\)，只需要知道其最长 Border 的长度 \(nxt_i\) 就可以得到其所有 Border（也就是 \(nxt[i]\)、\(nxt[nxt[i]]\)、\(nxt[nxt[nxt[i]]]\)……）。

现在的难点在于如何求出 \(nxt_i\)？

注意 Border 长度并不具有单调性，\(S[1\dots i]\) 是 \(S\) 的 Border 并不代表 \(S[1\dots i-1]\) 是 \(S\) 的 Border。所以不可以从小到大拓展 Border。

考虑从 \(i-1\) 的位置拓展过来。

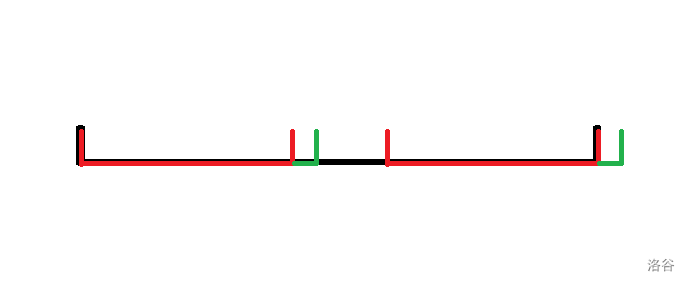
假设“红色+绿色”为 \(S[1\dots i]\)（“黑色+右侧绿色”） 的 Border，那么“红色”一定为 \(S[1\dots i-1]\)（"黑色"） 的 Border。

发现 \(S[1\dots i]\) 的所有 Border 都满足这个性质（包括最长 Border），但是 \(S[1\dots i-1]\) 的 Border 不一定可以在后面添加一个字符成为 \(S[1\dots i]\) 的 Border。

所以 \(nxt_i\) 直接从 \(nxt_{i-1}\) 继承长度，不断跳 \(nxt\) 找到更短的 \(S[1\dots i]\) 的 Border 直到这个 Border 拓展一个字符可以成为 \(S[1\dots i]\) 的 Border 后停下。

由于所有 Border 均满足上文所说性质，因此不会漏掉。

复杂度分析考虑 \(nxt_i\) 总增长量级即可。

做匹配的过程其实就是不断跳 \(nxt\) 的过程， 因为一个串的 Border 集合肯定包含它 Border 的 Border 集合，所以维护每个匹配状态最长的字符串一定不会漏掉匹配。

6. Manacher

目标：求出以 \(S\) 中每个字符为回文中心的最长回文串长度。

假设我们现在需要求 \(S\) 以每一个位置为中心的最长回文串的长度。

由于回文串的中心可能是字符也可能是两个字符之间的空白，因此在 \(S\) 相邻两个字符之间插入一个字符集之外的字符。这样就只需要求以字符为中心的回文串的长度了。

设 \(ext_i\) 表示以字符 \(i\) 为中心的最长回文串为 \(S[i-ext_i,i+ext_i]\)。

显然若 $S[i-x\dots i+x] $ 是回文串，那么 \(S[i-x+1\dots i+x-1]\) 也是回文串。因此可以对每个位置暴力拓展 \(ext_i\)，但是这样是 \(O(n^2)\) 的。

考虑一些回文串的性质，如下图：

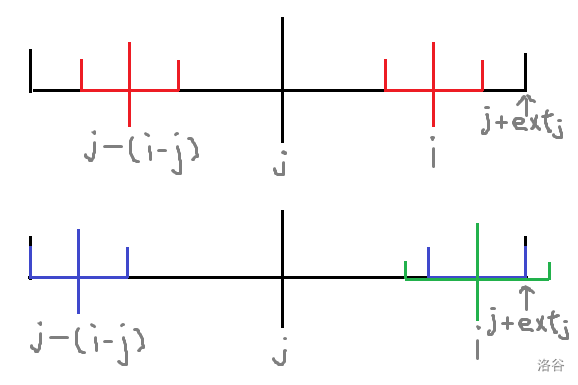
显然 \(j-(i-j)=2j-i\)。

当前需要求 \(ext_i\)，若存在一个 \(j\) 使得 \(j+ext_j\geq i\) 并且 \((2j-i)-ext_{2-j-i}> j-ext_j\)（没有碰到回文串的边界），此时 \(ext_i\) 一定恰好等于 \(ext_{2j-i}\)。

否则若 \((2j-i)-ext_{2-j-i}\leq j-ext_j\)，则 \(ext_i\) 可能不等于 \(ext_{2j-i}\)，但一定至少为 \((2j-i)-(j-ext_j)\)，也就是恰好卡在以 \(j\) 为回文串的边界处。

其实可以将上面两种情况合并，得到一个 \(ext_i\) 的下界，然后不断暴力扩展 \(ext_i\)。

但是怎么样才能保证时间复杂度为 \(O(n)\) 呢？注意到如果成功进行了暴力拓展，那么以 \(i\) 为中心的回文串范围一定会超出以 \(j\) 为中心的回文串的右端点。

那么只需要维护最大的 \(j+ext_j\) 以及对应的 \(j\)，这样每次暴力拓展的时候 \(j+ext_j\) 都会增加。并且一定有 \(j_ext_j\leq |S|\)，所以暴力拓展的次数至多为 \(|S|\) 次。

由于有暴力拓展，所以一定可以找到最长的合法的回文串。

7. exKMP（Z 函数）

目标：求出 \(S\) 与 \(S\) 的每个后缀的 LCP 长度 \(z_i\)。

exKMP 和 KMP 之间的关系就像 exCRT 和 CRT 之间的关系，不能说相差了太远，但至少也是隔了十万八千里。

显然 LCP 有单调性，所以一个暴力的想法单次 \(O(n)\) 求出一个 \(z_i\)。

类比于 Manacher 的思路，尝试考虑满足 \(j<i\) 的 \(j\) 是否能对求出 \(z_i\) 提供一些信息。

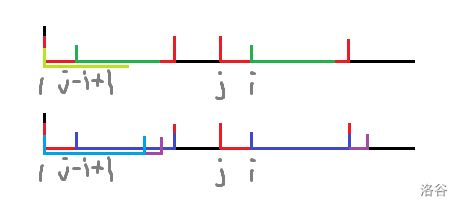
若 \(j+z_j-1\geq i\)（ \(S\) 和 \(S[j\dots n]\) 的 LCP（”红色“）覆盖到了位置 \(i\)），则进一步考虑 \(z_i\) 和 \(z_{j-i+1}\) 之间的大小关系。

稍微分析一下即可得出 \(z_i\geq \min(z_{j-i+1},j+z_j-i)\)，分析过程与 Manacher 的分析过程十分相似。

同样可以发现若维护 \(j+z_j-1\) 最大的 \(j\)，则当 \(z_i\) 暴力拓展时最大的 \(j+z_j-1\) 一定也会变大，所以总暴力拓展次数不超过 \(|S|\) 次。

一个应用是如何求 \(S\) 和 \(T\) 的每个后缀的 LCP 长度 \(p_i\)。

同样应用上述思想，维护 \(j+p_j-1\) 最大的 \(j\)，分析 \(p_i\) 与 \(j+p_j-1\) 和 \(z_{j-i+1}\) 的大小关系即可。暴力拓展次数不超过 \(|T|\) 次。