集成学习
什么是集成学习
集成学习通过建⽴⼏个模型来解决单⼀预测问题。它的⼯作原理是⽣成多个分类器/模型，各⾃独⽴地学习和作出预测。这些预测最后结合成组合预测，因此优于任何⼀个单分类的做出预测。
复习：机器学习的两个核⼼任务
- 任务⼀：主要⽤于解决⽋拟合问题
- 任务⼆：主要⽤于解决过拟合问题
集成学习中boosting和Bagging
只要单分类器的表现不太差，集成学习的结果总是要好于单分类器的
Bagging和随机森林
Bagging集成原理
⽬标：把下⾯的圈和⽅块进⾏分类
实现过程：
1) 采样不同数据集
2)训练分类器
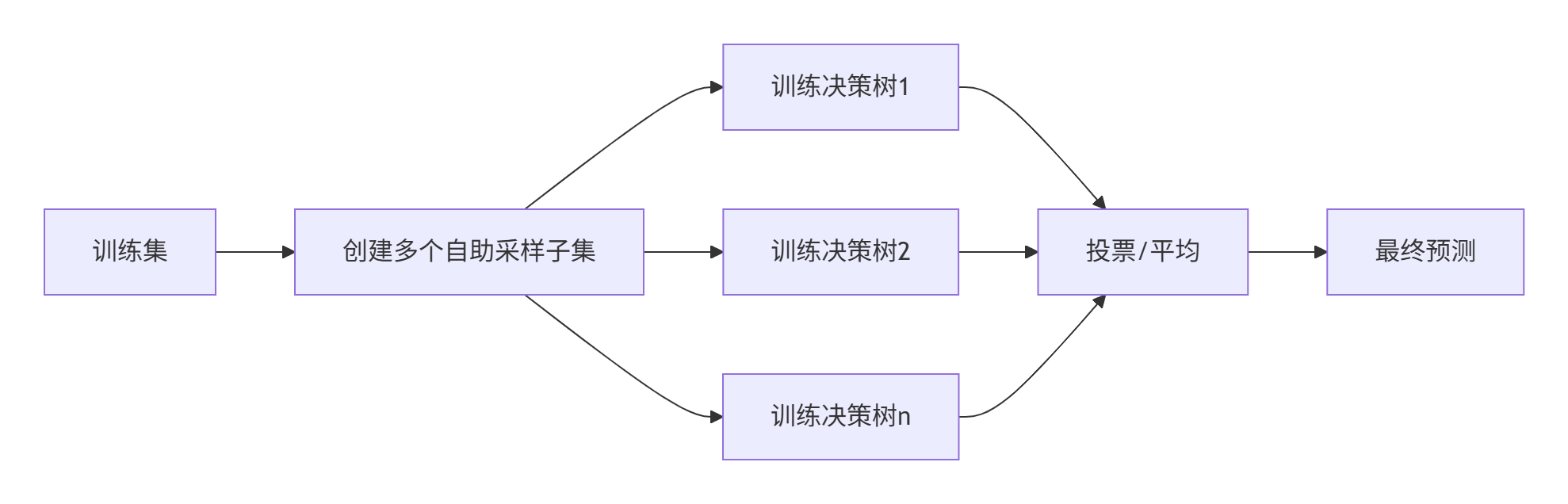
3)平权投票，获取最终结果
4)主要实现过程⼩结
bagging集成优点
Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法
经过上⾯⽅式组成的集成学习⽅法:
- 均可在原有算法上提⾼约2%左右的泛化正确率
- 简单, ⽅便, 通用
随机森林构造过程
在机器学习中，随机森林是⼀个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数⽽定。
随机森林 = Bagging + 决策树
例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个树的结果是False, 那么最终投票结果就是True
随机森林够造过程中的关键步骤(M表示特征数⽬)：
1)⼀次随机选出⼀个样本，有放回的抽样，重复N次(有可能出现重复的样本)
2) 随机去选出m个特征, m <<M，建⽴决策树
思考
- 1.为什么要随机抽样训练集？
- 如果不进⾏随机抽样，每棵树的训练集都⼀样，那么最终训练出的树分类结果也是完全⼀样的
- 2.为什么要有放回地抽样？
- 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，都是绝对“⽚⾯的”(当然这样说可能不对)，也就是说每棵树训练出来都是有很⼤的差异的；⽽随机森林最后分类取决于多棵树(弱分类器)的投票表决。
总结
随机森林通过构建多个决策树并集成它们的结果来提高模型性能：
- 随机性来源:
- 行随机性: Bagging (自助采样)
- 列随机性: 每次分割随机选择特征子集
- 关键优势:
- 处理高维数据能力
- 对噪声和异常值鲁棒
- 内置特征重要性评估
- 无需复杂特征缩放
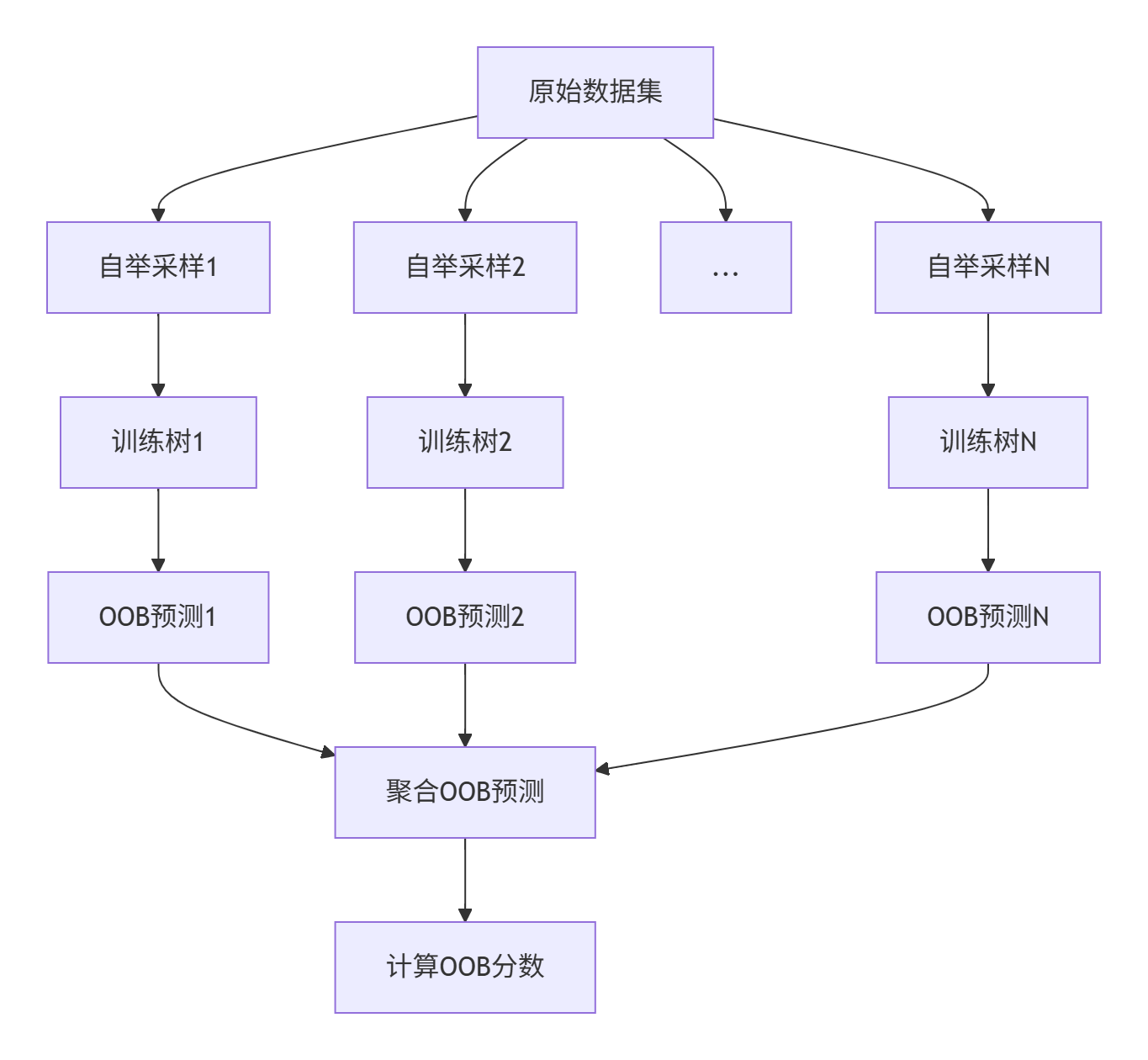
包外估计 (Out-of-Bag Estimate)oob
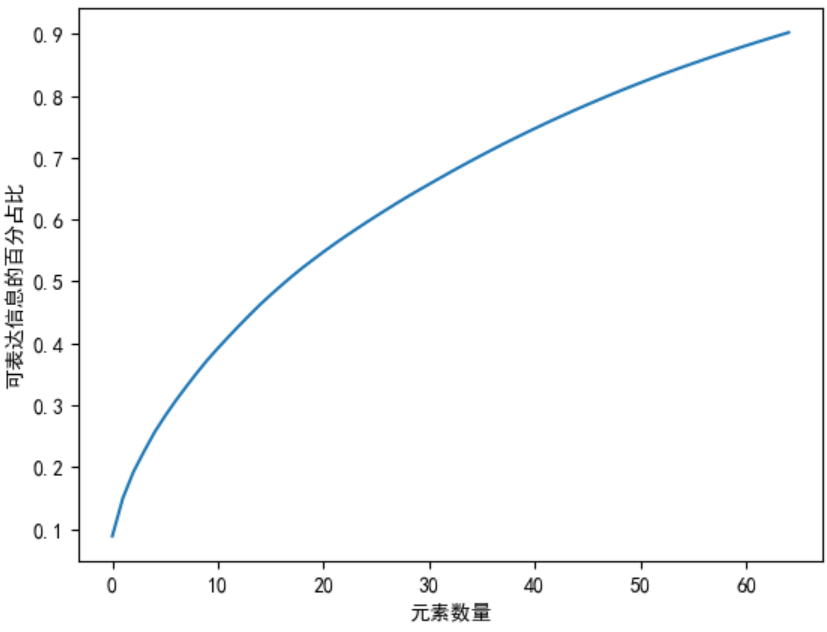
在随机森林构造过程中，如果进⾏有放回的抽样，我们会发现，总是有⼀部分样本我们选不到。
这部分数据，占整体数据的⽐重有多⼤呢？
这部分数据有什么⽤呢？
3.1 包外估计的定义
随机森林的 Bagging 过程，对于每⼀颗训练出的决策树 g t，与数据集 D 有如下关系：
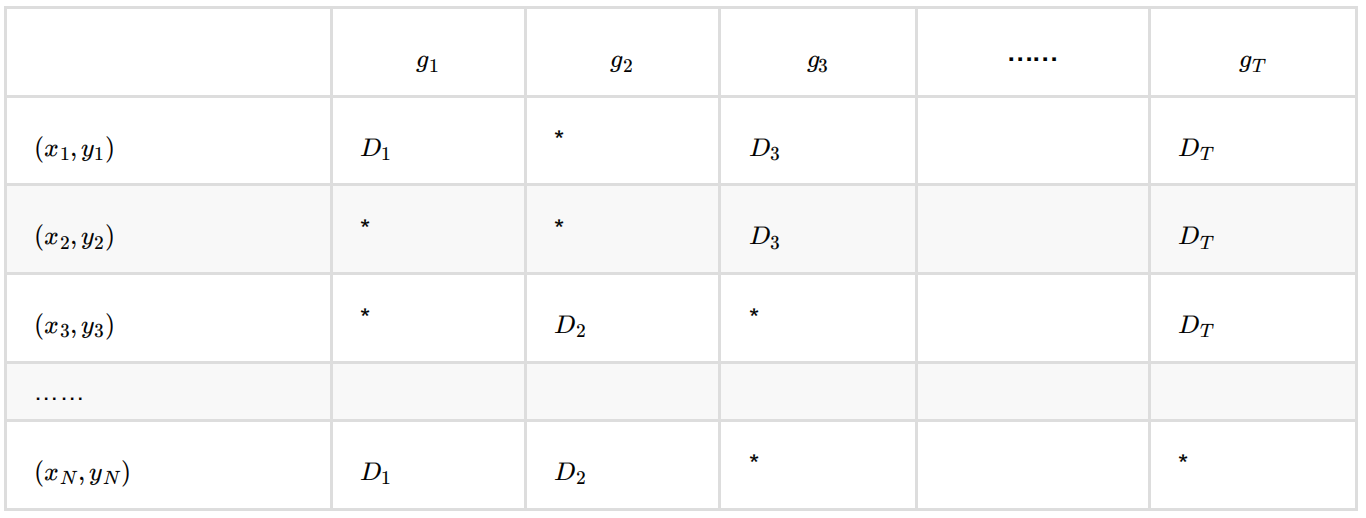
对于星号的部分，即是没有选择到的数据，称之为 Out-of-bag(OOB)数据，当数据⾜够多，对于任意⼀组数据 (x , y )是包外数据的概率为：
由于基分类器是构建在训练样本的⾃助抽样集上的，只有约 63.2％ 原样本集出现在中，⽽剩余的 36.8％ 的数据作为包外数据，可以⽤于基分类器的验证集。
经验证，包外估计是对集成分类器泛化误差的⽆偏估计.
在随机森林算法中数据集属性的重要性、分类器集强度和分类器间相关性计算都依赖于袋外数据。
3.2 包外估计的⽤途
- 当基学习器是决策树时，可使⽤包外样本来辅助剪枝 ，或⽤于估计决策树中各结点的后验概率以辅助对零训练样本结点的处理；（参见下文“oob_score的使用”）
- 当基学习器是神经⽹络时，可使⽤包外样本来辅助早期停⽌以减⼩过拟合 。
随机森林api介绍
sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True,random_state=None, min_samples_split=2)关键参数详解
1. 树的数量与复杂度
| 参数 | 默认值 | 推荐设置 | 作用 | 备注 |
|---|---|---|---|---|
n_estimators |
100 | 100-500 | 树的数量，越多越好但有边际效应 |
|
max_depth |
None | 5-30 或 None | 树的最大深度，None 表示无限扩展 | |
min_samples_split |
2 | 2-10 | 节点分裂所需最小样本数 |
|
min_samples_leaf |
1 | 1-5 | 叶节点所需最小样本数 |
|
2. 随机性与多样性控制
| 参数 | 默认值 | 推荐设置 | 作用 | 备注 |
|---|---|---|---|---|
max_features |
"auto" | "sqrt" 或 0.2-0.8 | 每棵树考虑的特征比例/数量 |
|
bootstrap |
True | True | 是否使用自助采样（放回抽样） | |
oob_score |
False | True | 是否计算袋外(OOB)分数 |
3. 效率优化参数
| 参数 | 默认值 | 推荐设置 | 作用 |
|---|---|---|---|
n_jobs |
None | -1 | 使用的CPU核心数 (-1 = 全部核心) |
random_state |
None | 固定值 | 确保结果可复现 |
verbose |
0 | 1 | 训练时显示进度信息 |
4.其他参数
Criterion：string，可选( {"gini", "entropy"}, default="gini")- 分割特征的测量⽅法
-
min_impurity_decrease: 节点分裂所需的最小不纯度减少值
-
- 计算方式：父节点不纯度 - 加权平均子节点不纯度
- 推荐值：0.0（默认）或1e-7至0.1之间（⼀般不推荐改动默认值1e-7。）
- 特点：
- 比基于样本数量的停止条件更灵活
- 对类别不平衡数据更有效
- 减少不重要分裂，防止过拟合
-
- 这个值限制了决策树的增⻓，如果某节点的不纯度(基于基尼系数，均⽅差)⼩于这个阈值，则该节点不再⽣成⼦节点。即为叶⼦节点 。
oob_score- 袋外分数评估- oob_score : bool, default=False
- 核心价值：
- 零成本验证：使用未被包含在训练集中的样本进行验证（约37%）
- 模型选择：替代交叉验证的高效选择
- 过拟合检测：比较训练分数和oob分数差距
- 特征重要性：计算基于oob的permutation importance
上⾯决策树参数中最重要的包括
- 最⼤特征数max_features，
- 最⼤深度max_depth，
- 内部节点再划分所需最⼩样本数min_samples_split
- 叶⼦节点最少样本数min_samples_leaf。
完整代码示例：
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score
# 创建示例数据集
X, y = make_classification(
n_samples=1000,
n_features=20,
n_classes=2,
random_state=42
)
# 数据分割
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# 创建并训练随机森林
rf = RandomForestClassifier(
n_estimators=300,
max_depth=15,
min_samples_leaf=3,
max_features='sqrt',
bootstrap=True,
oob_score=True,
n_jobs=-1,
random_state=42,
verbose=1
)
rf.fit(X_train, y_train)
# 模型评估
train_pred = rf.predict(X_train)
test_pred = rf.predict(X_test)
print(f"训练准确率: {accuracy_score(y_train, train_pred):.4f}")
print(f"测试准确率: {accuracy_score(y_test, test_pred):.4f}")
print(f"OOB分数: {rf.oob_score_:.4f}")
# 特征重要性分析
for i, importance in enumerate(rf.feature_importances_):
print(f"特征 {i}: {importance:.4f}")查看打印结果
训练准确率: 0.9712
测试准确率: 0.8950
OOB分数: 0.8950
特征 0: 0.0137
特征 1: 0.1052
特征 2: 0.0175
特征 3: 0.0111
特征 4: 0.0119
特征 5: 0.3607
特征 6: 0.0156
特征 7: 0.0123
特征 8: 0.0125
特征 9: 0.0101
特征 10: 0.0148
特征 11: 0.0231
特征 12: 0.0130
特征 13: 0.0128
特征 14: 0.0823
特征 15: 0.0124
特征 16: 0.0154
特征 17: 0.0115
特征 18: 0.2308
特征 19: 0.0135
注意
随机森林的建⽴过程
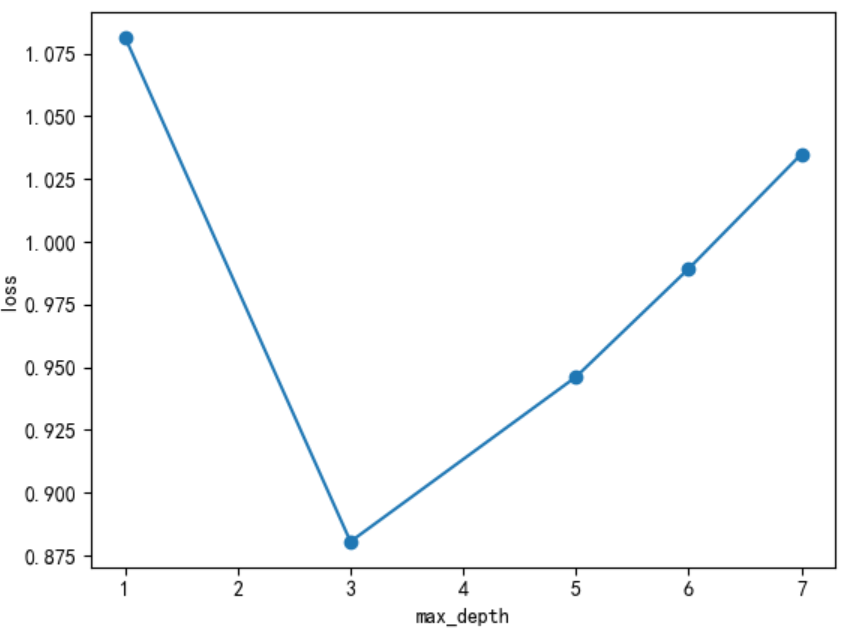
树的深度、树的个数等需要进⾏超参数调优
超参数调优策略
- 定义超参数的选择列表
param_grid = {
'n_estimators': [100, 200, 300],
'max_depth': [10, 20, 30, None],
'min_samples_split': [2, 5, 10],
'min_samples_leaf': [1, 2, 4]
}
# 使用 GridSearchCV 或 RandomizedSearchCV 搜索最佳参数param = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}- 使⽤GridSearchCV进⾏⽹格搜索
# 超参数调优
gc = GridSearchCV(rf, param_grid=param, cv=2)
gc.fit(x_train, y_train)
print("随机森林预测的准确率为：", gc.score(x_test, y_test))性能优化技巧
特征预排序:
# 启用内部优化，处理连续特征更高效
rf = RandomForestClassifier(ccp_alpha=0.0, min_impurity_decrease=0.0)内存与速度优化:
# 减小树的存储空间（在特征很多时特别有效）
rf = RandomForestClassifier(
memory='./rf_cache/', # 指定缓存目录
max_leaf_nodes=1000, # 限制叶节点数量
ccp_alpha=0.01 # 复杂度剪枝
)常见问题解决方案
-
过拟合问题：
# 解决方案：降低复杂度
rf = RandomForestClassifier(
max_depth=10,
min_samples_leaf=5,
min_samples_split=10,
max_features=0.5
)训练时间过长：
# 解决方案：使用子采样或特征选择
rf = RandomForestClassifier(
max_samples=0.5, # 使用50%样本
max_features=0.3, # 使用30%特征
n_jobs=-1
)类别不平衡处理：
# 解决方案：平衡采样策略
rf = RandomForestClassifier(
class_weight='balanced',
sampling_strategy='auto'
)高方差问题：
# 解决方案：增加树的数量和使用稳定参数
rf = RandomForestClassifier(
n_estimators=500,
max_depth=15,
oob_score=True,
random_state=42
)小结
bagging集成过程【知道】
- 1.采样 — 从所有样本⾥⾯，采样⼀部分
- 2.学习 — 训练弱学习器
- 3.集成 — 使⽤平权投票
随机森林介绍【知道】
- 随机森林定义
- 随机森林 = Bagging + 决策树
- 流程：
- 1.随机选取m条数据
- 2.随机选取k个特征
- 3.训练决策树
- 4.重复1-3
- 5.对上⾯的弱决策树进⾏平权投票
- 注意：
- 1.随机选取样本，且是有放回的抽取
- 2.选取特征的时候，选择m<<M，M是所有的特征数
- 包外估计
- 如果进⾏有放回的对数据集抽样，会发现，总是有⼀部分样本选不到；
- api
- sklearn.ensemble.RandomForestClassifier()
- Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习⽅法【了解】
- bagging的优点【了解】
- 1.均可在原有算法上提⾼约2%左右的泛化正确率
- 2.简单, ⽅便, 通⽤
Boosting
1什么是boosting
随着学习的积累从弱到强
简而言之：每新加入一个弱学习器，整体能力就会得到提升
代表算法：Adaboost，GBDT，XGBoost，LightGBM
2 实现过程：
1.训练第⼀个学习器
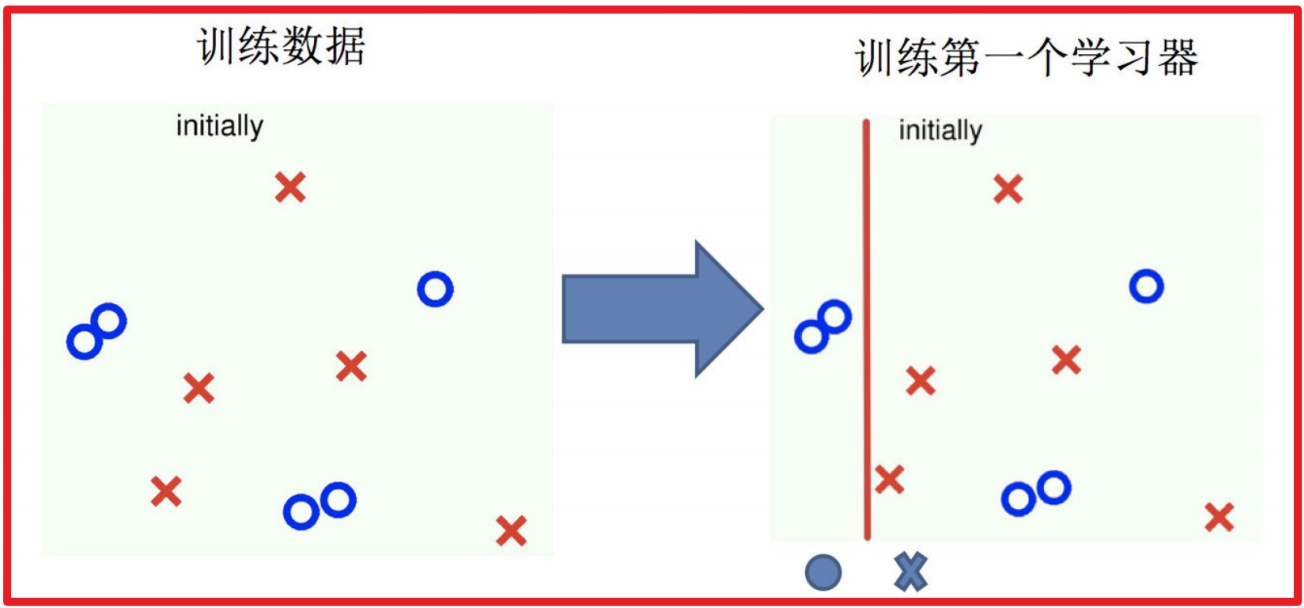
2.调整数据分布
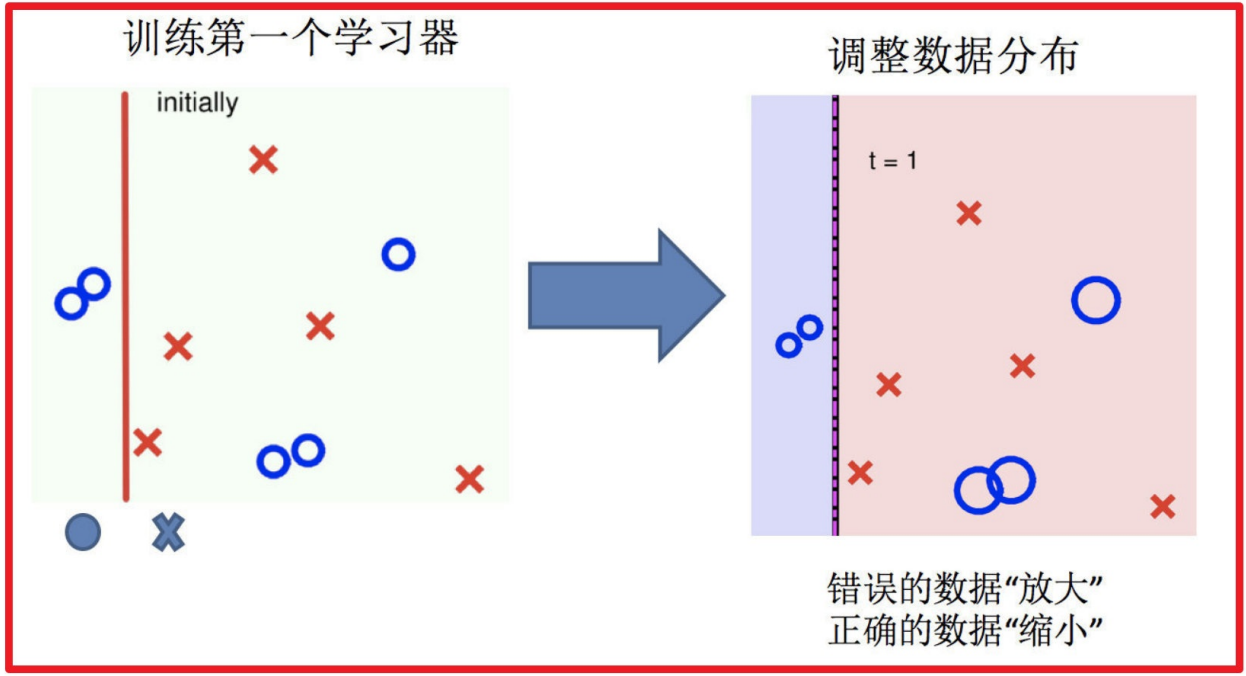
3.训练第⼆个学习器
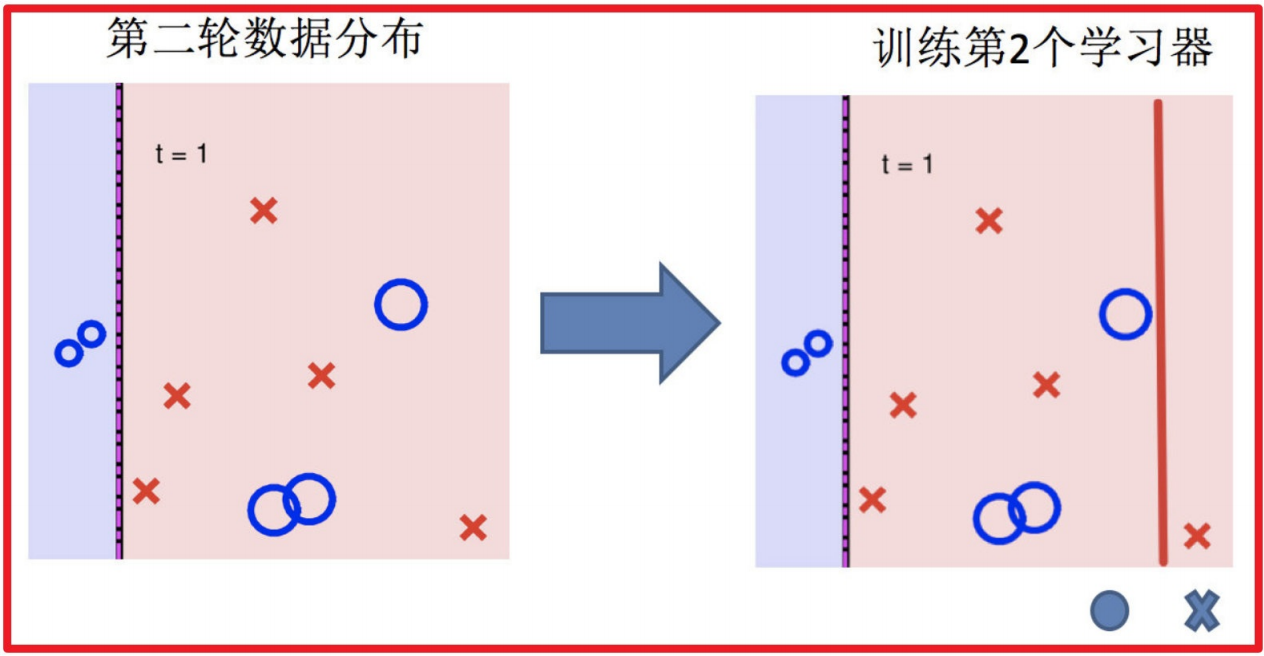
4.再次调整数据分布
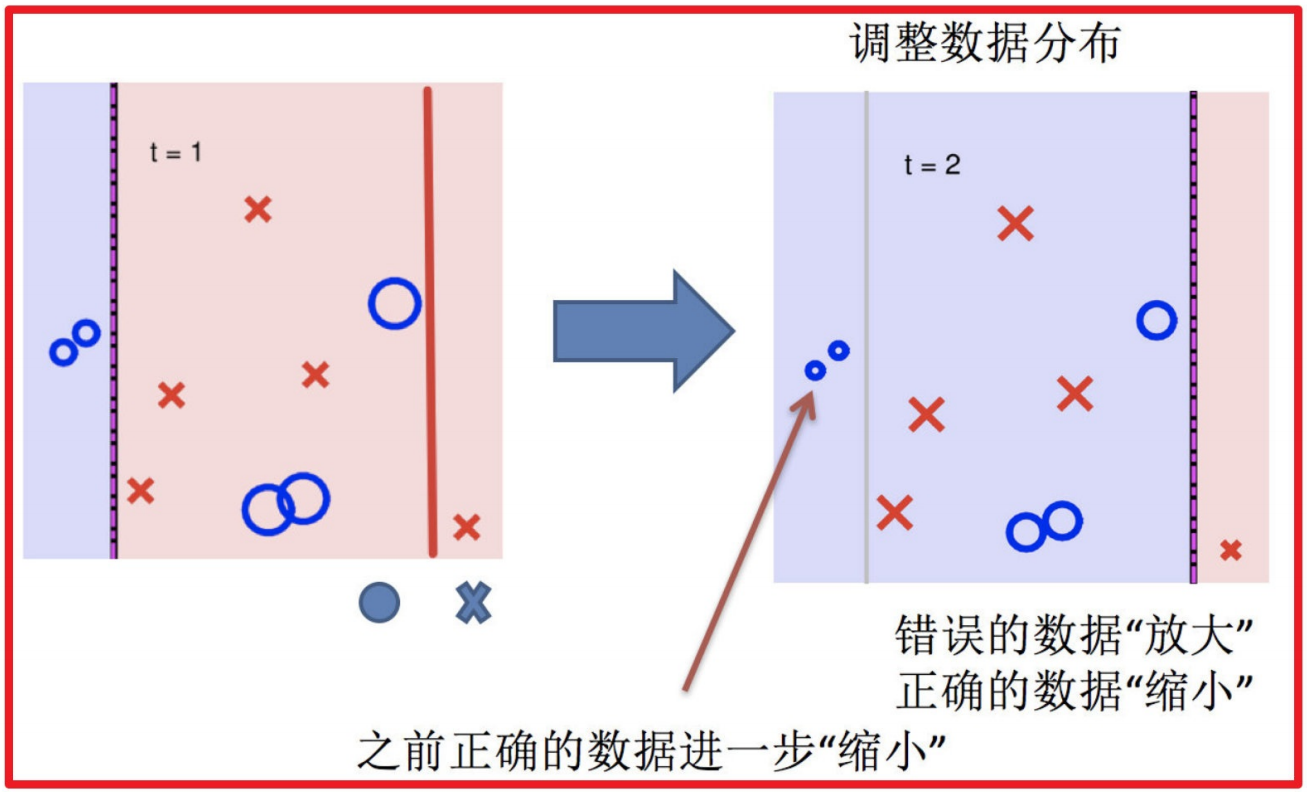
5.依次训练学习器，调整数据分布
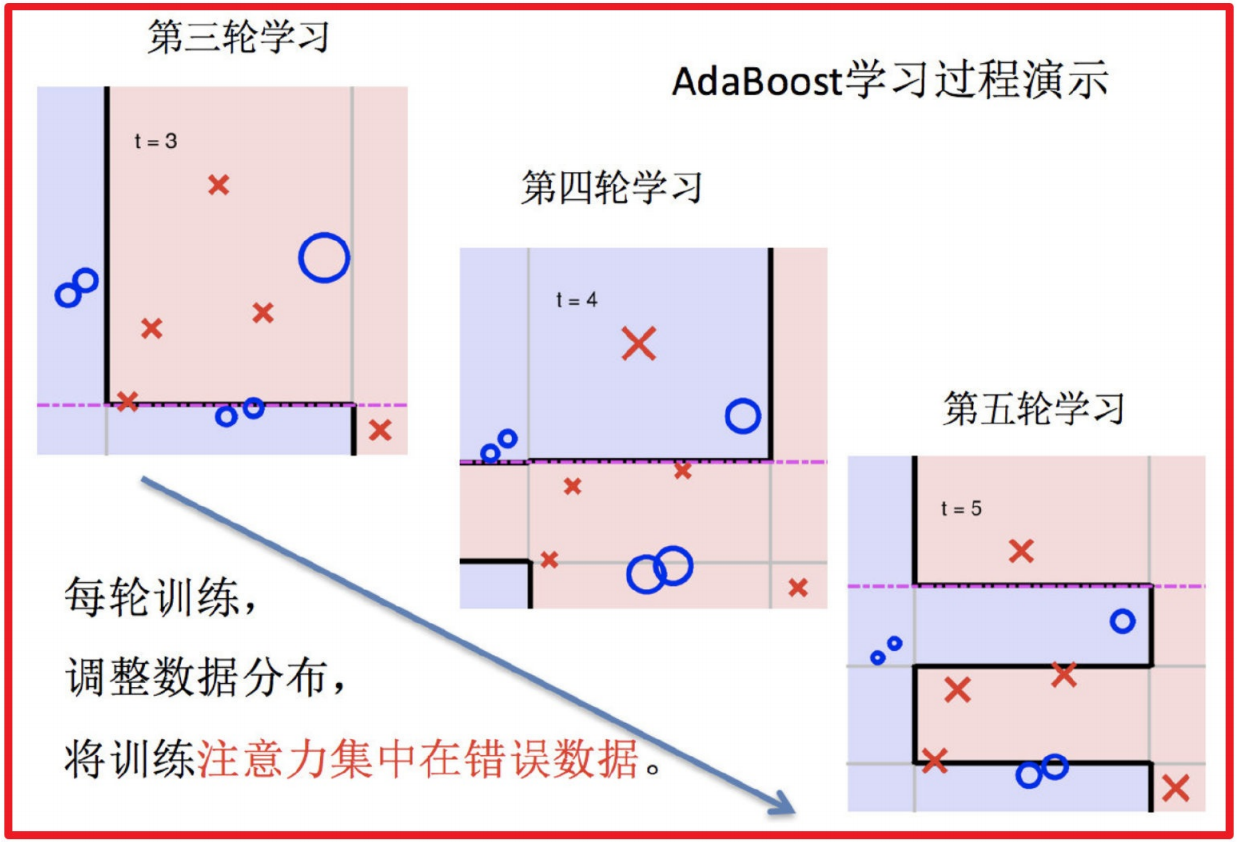
6.整体过程实现
3 bagging集成与boosting集成的区别：
- 区别⼀:数据⽅⾯
- Bagging：对数据进⾏采样训练；
- Boosting：根据前⼀轮学习结果调整数据的重要性。
- 区别⼆:投票⽅⾯
- Bagging：所有学习器平权投票；
- Boosting：对学习器进⾏加权投票。
- 区别三:学习顺序
- Bagging的学习是并⾏的，每个学习器没有依赖关系；
- Boosting学习是串⾏，学习有先后顺序。
- 区别四:主要作⽤
- Bagging主要⽤于提⾼泛化性能（解决过拟合，也可以说降低⽅差）
- Boosting主要⽤于提⾼训练精度 （解决⽋拟合，也可以说降低偏差）
AdaBoost介绍
4.1 构造过程细节
- 步骤⼀：初始化训练数据权重相等，训练第⼀个学习器。
- 该假设每个训练样本在基分类器的学习中作⽤相同，这⼀假设可以保证第⼀步能够在原始数据上学习基本分类器H 1(x)
- 步骤⼆：AdaBoost反复学习基本分类器，在每⼀轮m = 1, 2, ..., M 顺次的执⾏下列操作：
- （a） 在权值分布为D t 的训练数据上，确定基分类器；
- （b） 计算该学习器在训练数据中的错误率：
-
- （c） 计算该学习器的投票权重：
-
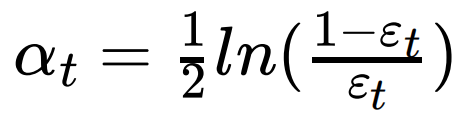
- （d） 根据投票权重，对训练数据重新赋权
-
-
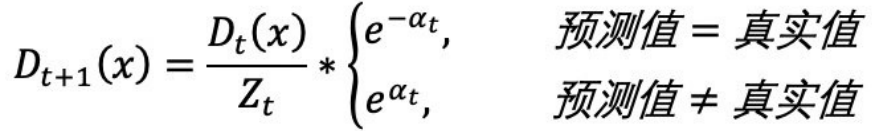
将下⼀轮学习器的注意⼒集中在错误数据上
-
数学原理：
-
-
-
-
αₜ 恒为正数
∵ αₜ = ½ ln[(1-εₜ)/εₜ] 且 εₜ < 0.5 (弱分类器有效性要求)
∴ 1-εₜ > εₜ ⇒ (1-εₜ)/εₜ > 1 ⇒ αₜ > 0
⇒e^(αₜ) > 1，e^(-αₜ) < 1 -
权重缩放方向
- 预测正确 → 乘以
e^(-αₜ) < 1→ 权重减小 - 预测错误 → 乘以
e^(αₜ) > 1→ 权重增大
- 预测正确 → 乘以
-
-
-
- 重复执⾏a到d步，m次；
- 步骤三：对m个学习器进⾏加权投票
4.2 关键点剖析
如何确认投票权重？
如何调整数据分布？
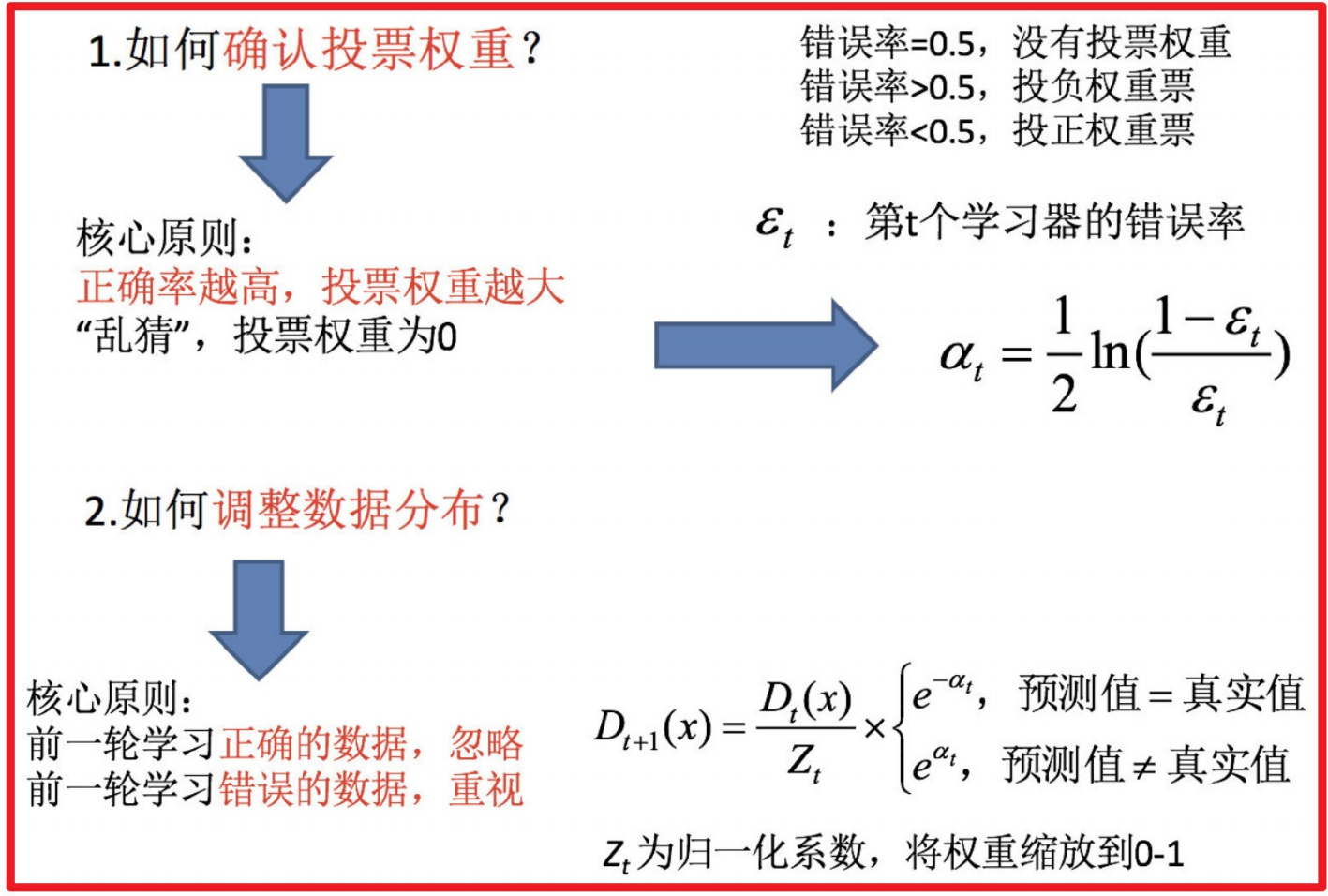
4.3 案例：
给定下⾯这张训练数据表所示的数据，假设弱分类器由xv产⽣，其阈值v使该分类器在训练数据集上的分类误差率最低，试⽤Adaboost算法学习⼀个强分类器。
问题解答：
步骤⼀：初始化训练数据权重相等，训练第⼀个学习器：
步骤⼆：AdaBoost反复学习基本分类器，在每⼀轮m = 1, 2, ..., M 顺次的执行下列操作：
当m=1的时候：
（a）在权值分布为D1的训练数据上，阈值v取2.5时分类误差率最低，故基本分类器为:
6,7,8被分错
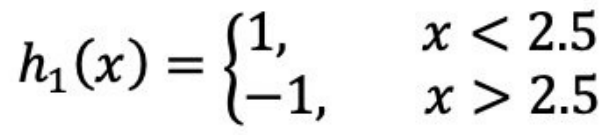
（b）计算该学习器在训练数据中的错误率：
（c）计算该学习器的投票权重：
（d）根据投票权重，对训练数据重新赋权:
根据下公式，计算各个权重值
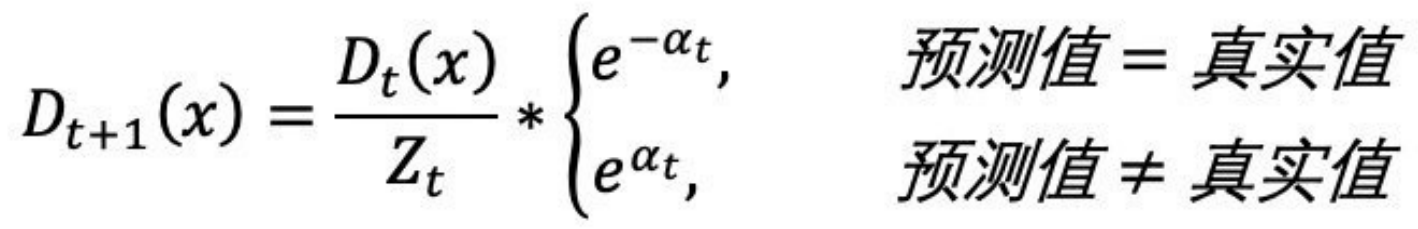
经计算得，D2的值为：
D 2 = (0.07143, 0.07143, 0.07143, 0.07143, 0.07143, 0.07143, 0.16667, 0.16667, 0.16667, 0.07143)
计算过程：
分类器H1(x)在训练数据集上有3个误分类点。
当m=2的时候：
（a）在权值分布为D2的训练数据上，阈值v取8.5时分类误差率最低，故基本分类器为:
3,4,5被分错
（b）计算该学习器在训练数据中的错误率：
（c）计算该学习器的投票权重：
（d）根据投票权重，对训练数据重新赋权:
经计算得，D 3 的值为：
D 3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.1667, 0.1060, 0.1060, 0.1060, 0.0455)
分类器H2(x)在训练数据集上有3个误分类点。
当m=3的时候：
（a）在权值分布为D3的训练数据上，阈值v取5.5时分类误差率最低，故基本分类器为:
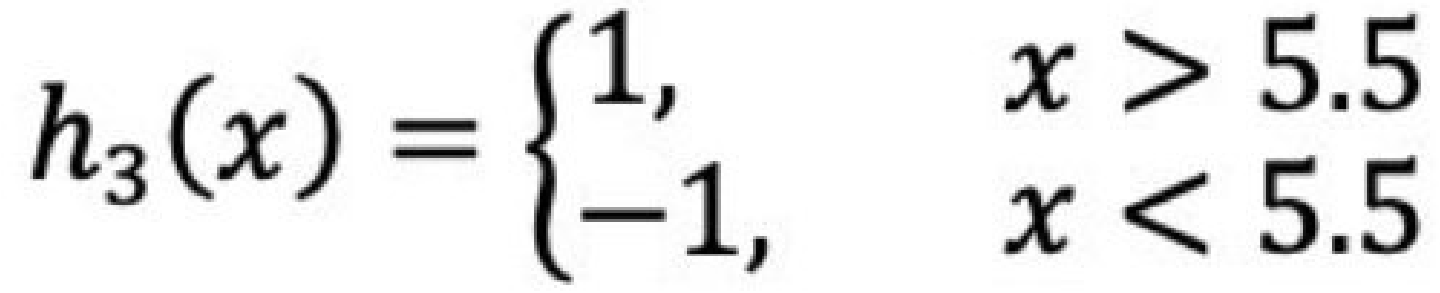
（b）计算该学习器在训练数据中的错误率：ε3 = 0.1820
（c）计算该学习器的投票权重：α3 = 0.7514
（d）根据投票权重，对训练数据重新赋权:
经计算得，D4的值为：
D4 = (0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125)
步骤三：对m个学习器进⾏加权投票,获取最终分类器
分类器H3(x)在训练数据集上的误分类点个数为0。
4.4 api介绍
from sklearn.ensemble import AdaBoostClassifier
5 ⼩结
- AdaBoost构造过程【知道】
- 步骤⼀：初始化训练数据权重相等，训练第⼀个学习器;
- 步骤⼆：AdaBoost反复学习基本分类器;
- 步骤三：对m个学习器进⾏加权投票
GBDT(梯度提升决策树）
GBDT 的全称是 Gradient Boosting Decision Tree，在传统机器学习算法中，GBDT算的上TOP3的算法。
-
Boosting（提升）： 属于集成学习的一种策略，通过串行训练多个弱学习器（通常是决策树），每个后续模型都专注于纠正前序模型的错误。
-
Gradient（梯度）： 利用损失函数的负梯度方向（下降最快的方向）作为当前模型需要拟合的目标（即“残差”的近似），这是其名称中“梯度”的来源。
-
Decision Tree（决策树）： 使用CART（分类与回归树）作为基础的弱学习器。
GBDT 是一种集成学习算法，通过迭代构建多个决策树来优化模型性能，核心思想是利用梯度下降来最小化损失函数。
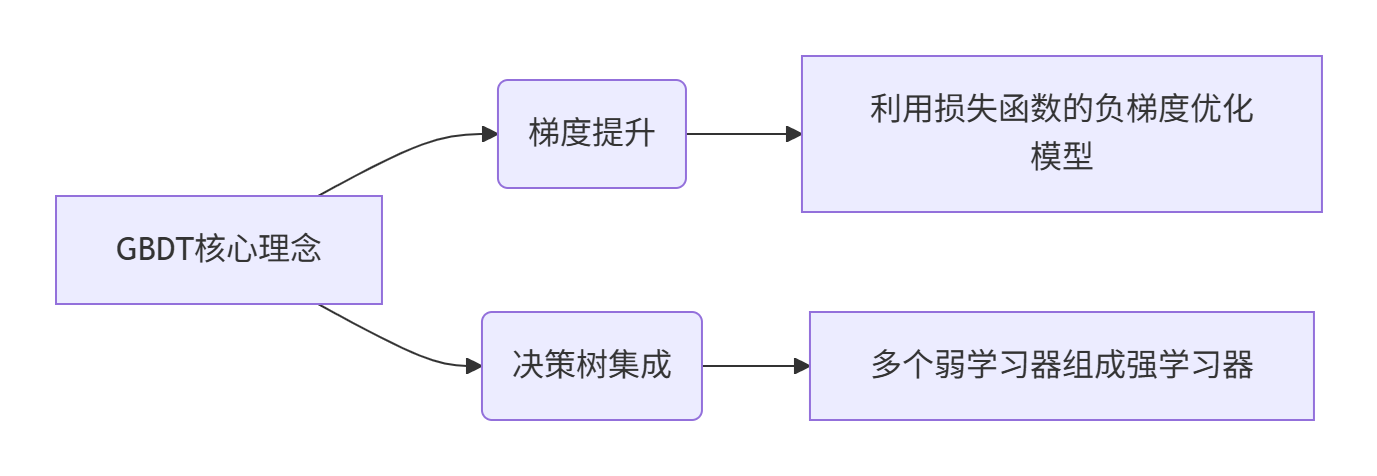
先来个通俗理解：假如有个⼈30岁，我们⾸先⽤20岁去拟合，发现损失有10岁，这时我们⽤6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们⽤3岁拟合剩下的差距，差距就只有⼀岁了。如果我们的迭代轮数还没有完，可以继续迭代下⾯，每⼀轮迭代，拟合的岁数误差都会减⼩。最后将每次拟合的岁数加起来便是模型输出的结果。
算法原理
GBDT 基于Boosting框架，通过迭代训练一系列弱学习器（决策树），每棵树学习的是之前所有树预测结果与真实值的残差（或梯度），最终将所有树的预测结果累加得到最终输出。
GBDT VS 传统Boosting
- AdaBoost：改变样本权重
- GBDT：拟合损失函数的负梯度
它在被提出之初就被认为是泛化能力(generalization)较强的算法。近些年更因为被用于搜索排序的机器学习模型而引起大家关注。
GBDT=梯度下降+Boosting+决策树
损失函数与伪残差
常见损失函数：
| 任务类型 | 损失函数 | 伪残差计算 |
|---|---|---|
| 回归 |
均方误差（MSE）、绝对误差（MAE）、L2损失: ½(y-ŷ)² |
y - ŷ |
| 二分类 | 对数损失: log(1+e^(-yŷ)) | y * (1 - sigmoid(ŷ)) |
| 多分类 | Softmax交叉熵 | y - softmax(ŷ) |
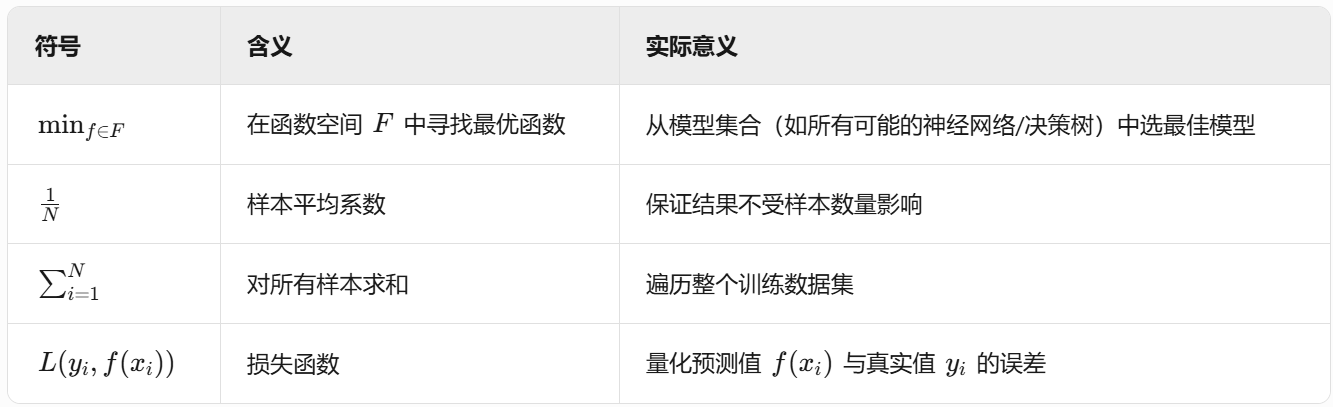
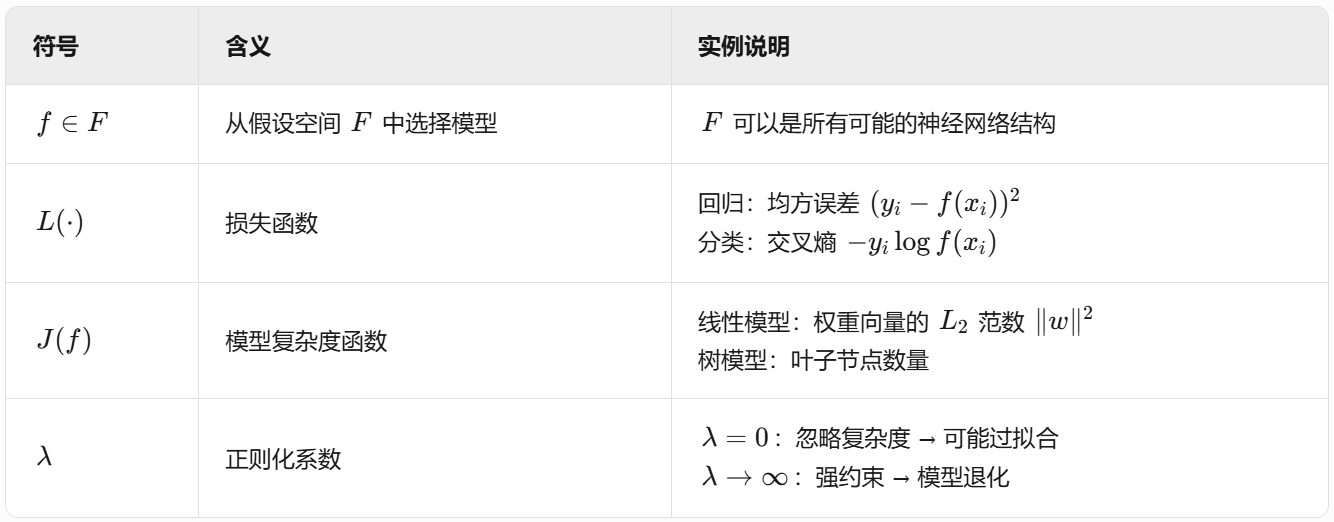
🎯 1. 损失函数（目标函数）
拟合残差rmi
📊 完整流程演示（房价预测示例）
| 样本 | 真实值 | 初始模型 | 残差 | 树1预测 | 更新后预测（λ=0.5） |
|---|---|---|---|---|---|
| A | 200 | 180 | +20 | +22 | 180+0.5×22=191 |
| B | 160 | 180 | -20 | -18 | 180+0.5×(-18)=171 |
| C | 190 | 180 | +10 | +12 | 180+0.5×12=186 |
迭代效果：
- 平均绝对误差从20万 → 降到9.5万（对比初始模型）
🔑 核心思想总结
-
残差学习
- 每棵树学习前序模型的预测残差
- 新树输入：特征
- 新树目标：残差
-
梯度下降本质
模型更新 fm=fm−1−λ∇L
-
- 负梯度 即残差方向
-
- 决策树作为函数逼近器计算梯度方向
-
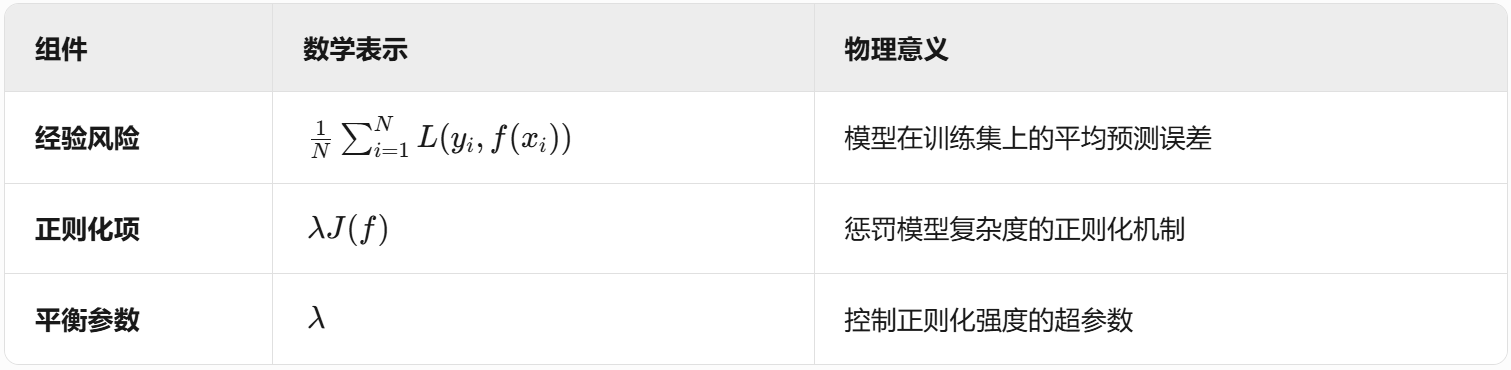
正则化机制
- 学习率 ：控制单棵树影响
- 树数量 ：限制复杂度
- 树深度：约束弱学习器表达能力
通过这种「串行构建残差修正器」的机制，GBDT能够逐步降低偏差，同时通过参数控制（λ, M, 树深度）避免过拟合。
示例代码
参数调优指南
关键超参数：
| 参数类型 | 参数 | 推荐值 | 作用 |
|---|---|---|---|
| 控制树结构 | max_depth | 3-10 | 树复杂度 |
| num_leaves | 20-120 | LightGBM特有 | |
| 防止过拟合 | learning_rate | 0.01-0.3 | 步长收缩 |
| subsample | 0.6-0.9 | 样本采样率 | |
| colsample_bytree | 0.6-0.9 | 特征采样率 | |
| 正则化 | reg_alpha | 0-0.5 | L1正则化 |
| reg_lambda | 0-1 | L2正则化 | |
| 迭代控制 | n_estimators | 100-5000 | 树的数量 |
| early_stopping | 50-100 | 早停轮数 |
GBDT 作为经典的集成学习算法，其思想启发了 XGBoost、LightGBM 等高效变种，在工业界和学术界仍被广泛应用。理解其原理对掌握现代机器学习模型具有重要意义。
GBDT变体与发展
-
XGBoost：极致优化效率与精度，支持并行、分布式计算。（kaggle竞赛神器） -
LightGBM：微软开发，基于直方图算法，速度快内存低。 -
CatBoost：自动处理类别特征，减少过拟合。
4.1 主要变体对比
| 算法 | 创新点 | 优势 |
|---|---|---|
| XGBoost |
增加正则项(γ,λ)控制复杂度； 精确贪婪算法 加权分位数 引入二阶导数信息，加速收敛； 支持并行计算（特征粒度并行） |
精确控制过拟合 处理稀疏数据 |
| LightGBM |
GOSS特征采样 使用直方图算法减少计算量； 基于 Leaf-wise 生长策略，减少树的深度； 支持类别特征直接处理。 |
训练速度快 内存消耗低 |
| CatBoost |
对称树结构 Ordered目标编码：引入有序提升（Ordered Boosting）减少偏差。 GPU优化 处理类别特征时减少噪声 |
处理类别特征 避免梯度偏移 |
实战应用
6.1 特征工程技巧
# GBDT特征处理特殊之处
1. 无需标准化：树模型对幅度不敏感
2. 缺失值处理：自动处理为单独分支
3. 类别特征：推荐使用one-hot编码(XGBoost)或标签编码(LightGBM)
4. 特征组合：通过树结构自动创建
# 特征重要性使用
model = LGBMClassifier().fit(X, y)
importances = model.feature_importances_6.2 LightGBM实际案例代码
# 使用LightGBM进行信用评分建模
import lightgbm as lgb
from sklearn.model_selection import train_test_split
# 数据准备
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
# 创建Dataset
train_data = lgb.Dataset(X_train, label=y_train, free_raw_data=False)
val_data = lgb.Dataset(X_val, label=y_val, reference=train_data)
# 参数设置
params = {
'objective': 'binary',
'metric': ['auc', 'binary_logloss'],
'num_leaves': 45,
'learning_rate': 0.08,
'feature_fraction': 0.75,
'bagging_fraction': 0.8,
'reg_alpha': 0.3,
'reg_lambda': 0.5
}
# 训练模型
model = lgb.train(
params,
train_data,
valid_sets=[val_data],
num_boost_round=1000,
early_stopping_rounds=50,
verbose_eval=20
)
# 解释模型
lgb.plot_importance(model, max_num_features=15)
lgb.plot_tree(model, tree_index=0, figsize=(20, 8))与随机森林（RF）的区别
| 特性 | GBDT | 随机森林 (RF) |
|---|---|---|
| 训练方式 | 串行（顺序添加树） | 并行（独立训练树） |
| 基学习器目标 | 拟合残差（错误） | 拟合原始标签 |
| 结果组合 | 加权求和 | 投票/平均 |
| 方差 vs 偏差 | 主要降低偏差 | 主要降低方差 |
| 过拟合风险 | 较高（需谨慎调参） | 较低（天然抗过拟合） |
| 数据敏感性 | 对噪声较敏感 | 更鲁棒 |
| 算法 | 核心差异 | 优势场景 |
|---|---|---|
| 随机森林 | 基于 Bagging，树间独立，通过随机采样降低方差。 | 大规模数据、并行计算 |
| Adaboost | 基于样本权重调整，每棵树关注前序错误样本。 | 二分类、简单特征场景 |
| GBDT | 基于梯度优化，每棵树拟合残差，对异常值更敏感（需预处理）。 | 高精度回归、复杂特征 |
优点总结
✅ 预测精度高：能有效处理非线性关系，在各类竞赛（如 Kaggle）中表现优异。
✅ 处理混合类型数据（数值+类别）
✅ 模型可解释性较好：通过特征重要性分析，能解释模型决策依据。
✅ 灵活支持自定义损失函数
缺点总结
❌ 训练时间较长（尤其树数量多时）：计算复杂度高，迭代训练需串行处理，难以并行（相比随机森林）。
❌ 超参数较多（学习率、树深度、子采样率等需调优）：调参复杂：需优化树的数量、深度、学习率等多个超参数。
❌ 对噪声和异常值较敏感：残差计算易受极端值影响，需提前处理。
❌ 串行训练难以完全并行化（但XGBoost/LightGBM优化了此问题）
总结
GBDT通过梯度提升框架将弱小的决策树组合成强大的模型，成为当前工业界表格数据建模的首选算法。现代实现如XGBoost、LightGBM和CatBoost在保持高精度的同时大幅优化了速度和内存效率。
未来发展趋势：
- 与深度学习的深度融合
- 自动机器学习集成
- 可解释性增强技术
- 高效分布式计算优化
在实际应用中，GBDT通常需要根据数据特性和计算资源选择合适的实现：
- 高精度需求 → XGBoost
- 大规模数据集 → LightGBM
- 类别特征丰富 → CatBoost
表示前t-1棵树组成的学习模型的预测误差。
的计算公式 ，用于确定梯度提升树中每个叶子节点的最佳预测值（权重）。
lightGBM
1.1 lightGBM演进过程
1.2 AdaBoost算法
AdaBoost是⼀种提升树的⽅法，和三个臭⽪匠，赛过诸葛亮的道理⼀样。
AdaBoost两个问题：
- (1) 如何改变训练数据的权重或概率分布
- 提⾼前⼀轮被弱分类器错误分类的样本的权重，降低前⼀轮被分对的权重
- (2) 如何将弱分类器组合成⼀个强分类器，亦即，每个分类器，前⾯的权重如何设置
- 采取”多数表决”的⽅法.加⼤分类错误率⼩的弱分类器的权重，使其作⽤较⼤，⽽减⼩分类错误率⼤的弱分类器的权重，使其在表决中起较⼩的作⽤。
1.3 GBDT算法以及优缺点
GBDT和AdaBosst很类似，但是⼜有所不同。
- GBDT和其它Boosting算法⼀样，通过将表现⼀般的几个模型（通常是深度固定的决策树）组合在⼀起来集成⼀个 表现较好的模型。
- AdaBoost是通过提升错分数据点的权重来定位模型的不足， Gradient Boosting通过负梯度来识别问题，通过计算负梯度来改进模型，即通过反复地选择⼀个指向负梯度⽅向的函数，该算法可被看做在函数空间⾥对⽬标函数进⾏优化。
缺点：
GBDT ->预排序⽅法(pre-sorted)
- (1) 空间消耗⼤。
- 这样的算法需要保存数据的特征值，还保存了特征排序的结果（例如排序后的索引，为了后续快速的计算分割点），这⾥需要消耗训练数据两倍的内存。
- (2) 时间上也有较⼤的开销。
- 在遍历每⼀个分割点的时候，都需要进⾏分裂增益的计算，消耗的代价⼤。
- (3) 对内存(cache)优化不友好。
- 在预排序后，特征对梯度的访问是⼀种随机访问，并且不同的特征访问的顺序不⼀样，⽆法对cache进⾏优化。
- 同时，在每⼀层⻓树的时候，需要随机访问⼀个⾏索引到叶⼦索引的数组，并且不同特征访问的顺序也不⼀样，也会造成较⼤的cache miss。
1.4 启发
常⽤的机器学习算法，例如神经⽹络等算法，都可以以mini-batch的⽅式训练，训练数据的大小不会受到内存限制。
⽽GBDT在每⼀次迭代的时候，都需要遍历整个训练数据多次。
如果把整个训练数据装进内存则会限制训练数据的⼤⼩；如果不装进内存，反复地读写训练数据⼜会消耗⾮常⼤的时间。
尤其⾯对⼯业级海量的数据，普通的GBDT算法是不能满⾜其需求的。
LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题，让GBDT可以更好更快地⽤于⼯业实践。
2 什么是lightGBM
lightGBM是2017年1⽉，微软在GItHub上开源的⼀个新的梯度提升框架。
在开源之后，就被别⼈冠以“速度惊⼈”、“⽀持分布式”、“代码清晰易懂”、“占⽤内存⼩”等属性。
LightGBM主打的⾼效并⾏训练让其性能超越现有其他boosting⼯具。在Higgs数据集上的试验表明，LightGBM⽐XGBoost快将近10倍，内存占⽤率⼤约为XGBoost的1/6。
higgs数据集介绍：这是⼀个分类问题，⽤于区分产⽣希格斯玻⾊⼦的信号过程和不产⽣希格斯玻⾊⼦的信号过程。
3 lightGBM原理
lightGBM 主要基于以下方面优化，提升整体特特性：
- 基于Histogram（直⽅图）的决策树算法
- Lightgbm 的Histogram（直⽅图）做差加速
- 带深度限制的Leaf-wise的叶⼦⽣⻓策略
- 直接⽀持类别特征
- 直接⽀持⾼效并⾏
具体解释⻅下，分节介绍。
3.1 基于Histogram（直方图）的决策树算法
直⽅图算法的基本思想是
- 把连续的浮点特征值离散化成k个整数，同时构造⼀个宽度为k的直⽅图。
- 在遍历数据的时候，根据离散化后的值作为索引在直⽅图中累积统计量，当遍历⼀次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点。
Eg：
[0, 0.1) --> 0;
[0.1,0.3) --> 1;
...
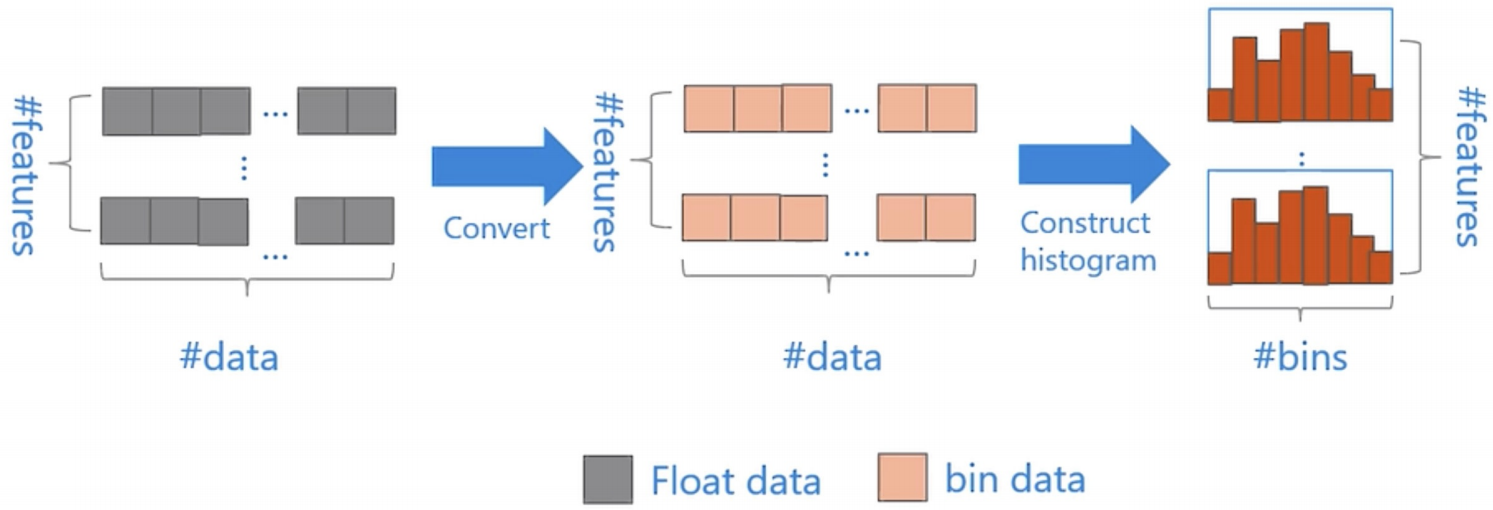
使⽤直⽅图算法有很多优点。⾸先，最明显就是内存消耗的降低，直⽅图算法不仅不需要额外存储预排序的结果，⽽且可以只保存特征离散化后的值，⽽这个值⼀般⽤8位整型存储就⾜够了，内存消耗可以降低为原来的1/8。
然后在计算上的代价也大幅降低，预排序算法每遍历⼀个特征值就需要计算⼀次分裂的增益，⽽直⽅图算法只需要计算k次（k可以认为是常数），时间复杂度从O(#data#feature)优化到O(k#features)。
当然，Histogram算法并不是完美的。由于特征被离散化后，找到的并不是很精确的分割点，所以会对结果产⽣影响。
但在不同的数据集上的结果表明，离散化的分割点对最终的精度影响并不是很⼤，甚⾄有时候会更好⼀点。原因是决策树本来就是弱模型，分割点是不是精确并不是太重要；较粗的分割点也有正则化的效果，可以有效地防⽌过拟合；即使单棵树的训练误差⽐精确分割的算法稍⼤，但在梯度提升（Gradient Boosting）的框架下没有太⼤的影响。
3.2 Lightgbm 的Histogram（直方图）做差加速
⼀个叶⼦的直⽅图可以由它的⽗亲节点的直⽅图与它兄弟的直⽅图做差得到。
通常构造直⽅图，需要遍历该叶⼦上的所有数据，但直⽅图做差仅需遍历直⽅图的k个桶。
利⽤这个⽅法，LightGBM可以在构造⼀个叶⼦的直⽅图后，可以⽤⾮常微⼩的代价得到它兄弟叶⼦的直⽅图，在速度上可以提升⼀倍。
3.3 带深度限制的Leaf-wise的叶⼦⽣⻓策略
Level-wise遍历⼀次数据可以同时分裂同⼀层的叶⼦，容易进⾏多线程优化，也好控制模型复杂度，不容易过拟合。
- 但实际上Level-wise是⼀种低效的算法，因为它不加区分的对待同⼀层的叶⼦，带来了很多没必要的开销，因为实际上很多叶⼦的分裂增益较低，没必要进⾏搜索和分裂。
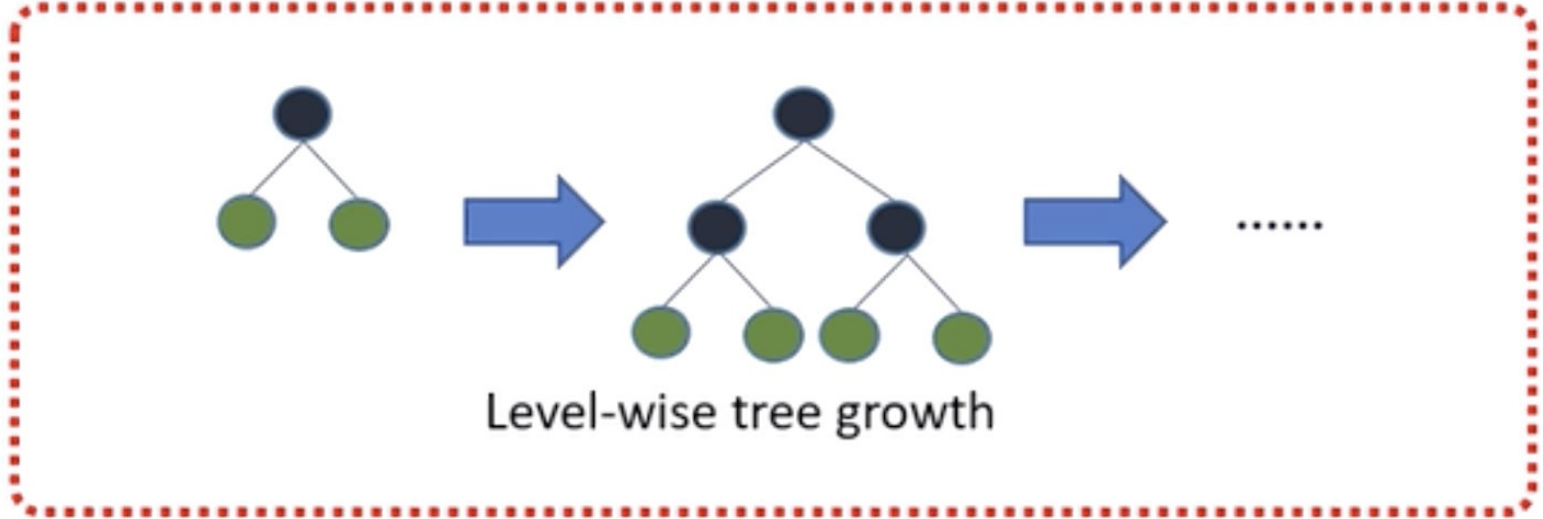
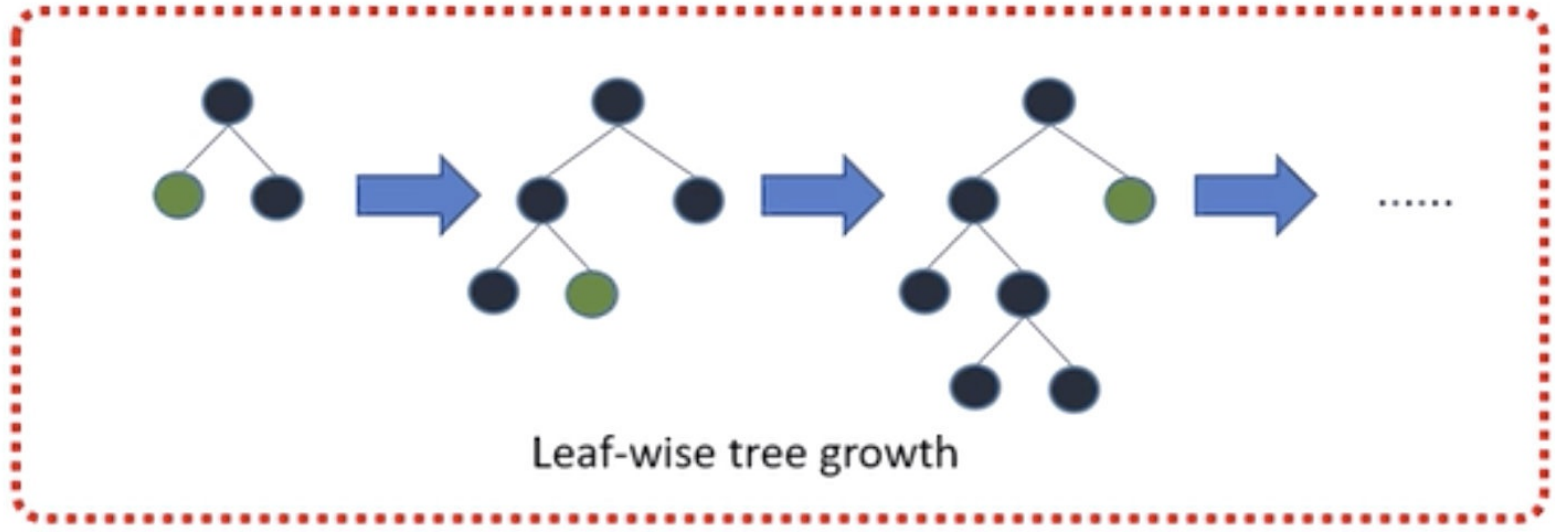
Leaf-wise则是⼀种更为⾼效的策略，每次从当前所有叶⼦中，找到分裂增益最⼤的⼀个叶⼦，然后分裂，如此循环。
- 因此同Level-wise相⽐，在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度。
- Leaf-wise的缺点是可能会⻓出⽐较深的决策树，产⽣过拟合。因此LightGBM在Leaf-wise之上增加了⼀个最⼤深度的限制，在保证⾼效率的同时防⽌过拟合。
3.4 直接支持类别特征
实际上⼤多数机器学习⼯具都⽆法直接⽀持类别特征，⼀般需要把类别特征，转化到多维的0/1特征，降低了空间和时间的效率。
⽽类别特征的使⽤是在实践中很常⽤的。基于这个考虑，LightGBM优化了对类别特征的⽀持，可以直接输⼊类别特征，不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。
在Expo数据集上的实验，相⽐0/1展开的⽅法，训练速度可以加速8倍，并且精度⼀致。⽬前来看，LightGBM是第⼀个直接⽀持类别特征的GBDT⼯具。
Expo数据集介绍：数据包含1987年10⽉⾄2008年4⽉美国境内所有商业航班的航班到达和离开的详细信息。这是⼀个庞⼤的数据集：总共有近1.2亿条记录。主要⽤于预测航班是否准时。
3.5 直接支持高效并行
LightGBM还具有⽀持⾼效并⾏的优点。LightGBM原⽣⽀持并⾏学习，⽬前⽀持特征并⾏和数据并⾏的两种。
- 特征并⾏的主要思想是在不同机器在不同的特征集合上分别寻找最优的分割点，然后在机器间同步最优的分割点。
- 数据并⾏则是让不同的机器先在本地构造直⽅图，然后进⾏全局的合并，最后在合并的直⽅图上⾯寻找最优分割点。
LightGBM针对这两种并⾏⽅法都做了优化:
- 在特征并行算法中，通过在本地保存全部数据避免对数据切分结果的通信；
- 在数据并⾏中使⽤分散规约 (Reduce scatter) 把直⽅图合并的任务分摊到不同的机器，降低通信和计算，并利⽤直⽅图做差，进⼀步减少了⼀半的通信量。
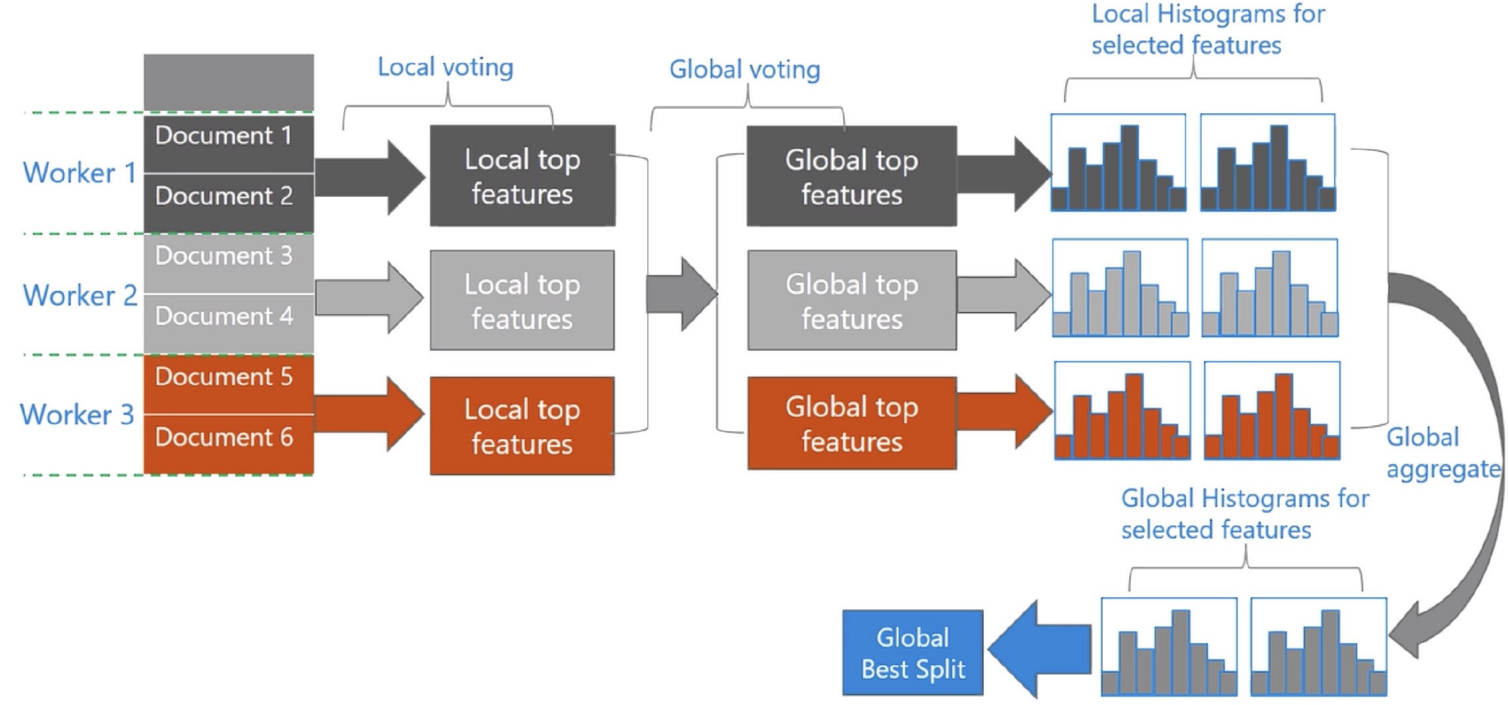
- 基于投票的数据并行(Voting Parallelization)则进⼀步优化数据并⾏中的通信代价，使通信代价变成常数级别。在数据量很⼤的时候，使⽤投票并⾏可以得到⾮常好的加速效果。
LightGBM优势
- 基于Histogram（直⽅图）的决策树算法
- Lightgbm 的Histogram（直⽅图）做差加速
- 带深度限制的Leaf-wise的叶⼦⽣⻓策略
- 直接⽀持类别特征
- 直接⽀持⾼效并⾏
lightGBM算法api介绍
1 lightGBM的安装
- windows下：
pip install lightgbm
- mac下：
接下来，通过鸢尾花数据集对lightGBM的基本使⽤，做⼀个介绍。
# 加载数据，对数据进⾏基本处理
data=load_iris()
x=data.data
y=data.target
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# 模型训练
gbm = lgb.LGBMRegressor(objective='regression', learning_rate=0.05, n_estimators=200)
# gbm.fit(X_train, y_train, eval_set=[(X_test, y_test)], eval_metric='l1',early_stopping_rounds=5)
# 自LightGBM 3.0版本起，early_stopping_rounds参数已从模型构造函数移至fit()方法的callbacks参数中。需要使用回调函数实现早停。
#启用早停需要：必须设置足够大的n_estimators：n_estimators=1000 # 初始值需大于早停轮数
gbm.fit(X_train, y_train, eval_set=[(X_test, y_test)], eval_metric='l1',callbacks=[lgb.early_stopping(stopping_rounds=5)])
print(f"实际使用迭代次数: {gbm.best_iteration_}") # 早停发生的轮次
print(f"最佳验证分数: {gbm.best_score_['valid_0']['l1']}")
gbm.score(X_test, y_test)
# 0.810605595102488点击查看打印结果
[LightGBM] [Info] Auto-choosing col-wise multi-threading, the overhead of testing was 0.000028 seconds.
You can set `force_col_wise=true` to remove the overhead.
[LightGBM] [Info] Total Bins 87
[LightGBM] [Info] Number of data points in the train set: 120, number of used features: 4
[LightGBM] [Info] Start training from score 0.975000
[LightGBM] [Warning] No further splits with positive gain, best gain: -inf
Training until validation scores don't improve for 5 rounds
[LightGBM] [Warning] No further splits with positive gain, best gain: -inf
[LightGBM] [Warning] No further splits with positive gain, best gain: -inf
...省略...
[LightGBM] [Warning] No further splits with positive gain, best gain: -inf
Early stopping, best iteration is:
[92] valid_0's l1: 0.0909559 valid_0's l2: 0.0403314
实际使用迭代次数: 92
最佳验证分数: 0.09095594373649211
0.9415486955284025当然，如果最大迭代次数设置过小，也会无法触发早停：
gbm = lgb.LGBMRegressor(objective='regression', learning_rate=0.05, n_estimators=10)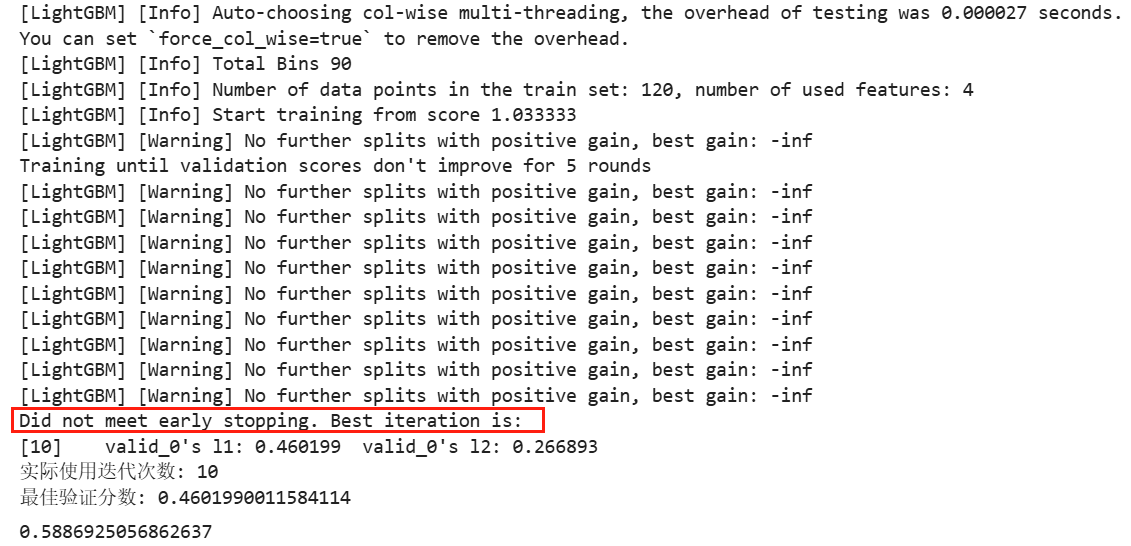
# ⽹格搜索，参数优化
estimator = lgb.LGBMRegressor(num_leaves=31)
param_grid = {
'learning_rate': [0.01, 0.1, 1],
'n_estimators': [20, 40]
}
gbm = GridSearchCV(estimator, param_grid, cv=4)
gbm.fit(X_train, y_train)
print('Best parameters found by grid search are:', gbm.best_params_)
# Best parameters found by grid search are: {'learning_rate': 0.1, 'n_estimators': 40}模型调优训练
gbm = lgb.LGBMRegressor(num_leaves=31, learning_rate=0.1, n_estimators=40)
gbm.fit(X_train, y_train, eval_set=[(X_test, y_test)], eval_metric='l1', callbacks=[lgb.early_stopping(stopping_rounds=5)])
gbm.score(X_test, y_test)
# 0.9536626296481988lightgbm综合案例：
《绝地求生》玩家排名预测
当前最流行的集成学习框架分析
🔥 最流行且实用的集成学习框架
当前工业界最流行的集成学习框架主要有三个主流选择：
-
XGBoost (eXtreme Gradient Boosting)
- 仍然是最广泛使用的框架之一
- 在Kaggle竞赛中多年占据主导地位
- GitHub stars: 24.5k+
-
LightGBM (Light Gradient Boosting Machine)
- 微软开发的高效框架
- 在工业界大规模应用占比快速提升
- GitHub stars: 16.2k+
-
CatBoost (Categorical Boosting)
- 由Yandex开发的强力框架
- 专门优化了类别特征处理
- GitHub stars: 7.5k+
🏆 实际工作中使用情况
根据2023年数据科学家调查报告和工业界实践：
| 框架 | 企业采用率 | 主要优势 | 典型应用场景 |
|---|---|---|---|
| LightGBM | 约58% | 极快的训练速度，低内存消耗 | 大规模数据，实时预测系统 |
| XGBoost | 约46% | 卓越的精度，丰富的特性 | 结构化数据竞赛，金融风控 |
| CatBoost | 约32% | 自动处理类别特征，鲁棒性强 | 用户行为预测，推荐系统 |
| Scikit-Learn RF | 30% | 简单易用，集成方便 | 快速原型开发 |
注：总和超过100%因为很多公司使用多种框架
性能对比
# 基准测试数据(Microsoft, 2017)
+-----------------+-----------+------------+------------+
| Algorithm | Accuracy | Train Time | Memory Use |
+-----------------+-----------+------------+------------+
| XGBoost | 92.1% | 38min | 15.2GB |
| LightGBM | 92.3% | 11min | 4.3GB |
| CatBoost | 92.5% | 22min | 8.7GB |
+-----------------+-----------+------------+------------+XGBoost的深度分析
✅ XGBoost的优势
-
卓越的性能表现
- 在结构化数据上的预测精度通常是最高的
- 大量Kaggle竞赛获胜解决方案的核心算法
-
丰富的功能
- 支持多种目标函数（回归/分类/排序）
- 自定义损失函数
- 正则化控制过拟合
- 缺失值自动处理
-
生态系统成熟
- 完善的文档和教程
- 多种语言支持（Python/R/Java等）
- 与MLflow等MLOps工具深度集成
-
调优灵活性
- 丰富的超参数（50+）
- 交叉验证内置支持
- 提前停止功能
⚠️ XGBoost的局限
-
内存消耗大
- 相比LightGBM内存使用更高
- 不适合超大规模数据集（1亿+样本）
-
训练速度较慢
- LightGBM通常比XGBoost快3-10倍
- CatBoost在GPU上的优势明显
-
特征工程需求高
- 对类别特征处理不如CatBoost智能
- 需要手动特征编码
🚀 XGBoost在实际工作中的应用建议
-
推荐使用场景
-
替代方案考虑
-
调优技巧
- 优先调优learning_rate, max_depth, n_estimators
- 使用早停法确定最佳迭代次数
现代集成学习框架最佳实践
-
框架选择策略
-
生产部署优化
- 模型压缩（XGBoost pruning）
- ONNX格式转换
- 使用Triton Inference Server
-
自动化ML集成
应用场景
| 场景 | 应用案例 | 模型选择 |
|---|---|---|
| 金融风控 | 信用评分、反欺诈 | XGBoost+严格特征解释 |
| 广告CTR预测 | 点击率预估 | LightGBM(大规模数据) |
| 推荐系统 | 个性化推荐 | GBDT+LR混合模型 |
| 医疗诊断 | 疾病预测 | CatBoost(处理医疗分类变量) |
| 工业预测 | 设备故障预测 | 时间序列GB |
总结建议
-
首选框架：对于大多数工业场景，LightGBM是当前最实用、最高效的首选框架，平衡了速度、精度和资源消耗
-
XGBoost定位：在精度要求极高的场景（如金融风控）和有成熟XGBoost基础设施的公司中，XGBoost仍是不可替代的选择
-
新兴趋势：
- CatBoost在类别特征多的场景表现卓越
- 分布式版本（Dask-XGBoost, LightGBM on Spark）适合超大数据
- 框架融合（ensemble of ensembles）成为高阶技术
建议学习路径：LightGBM → XGBoost → CatBoost → 定制集成
扩展内容
无偏估计
1.如何理解⽆偏估计
⽆偏估计：就是我认为所有样本出现的概率⼀样。
假如有N种样本我们认为所有样本出现概率都是1/N。然后根据这个来计算数学期望。此时的数学期望就是我们平常讲的平均值。
数学期望本质就是平均值
2.⽆偏估计为何叫做“⽆偏”？它要“估计”什么？
⾸先回答第⼀个问题：它要“估计”什么？
- 它要估计的是整体的数学期望（平均值）。
第⼆个问题：那为何叫做⽆偏？有偏是什么？
- 假设这个是⼀些样本的集合X = x 1, x 2 , x 3, ..., x N，我们根据样本估计整体的数学期望（平均值）。
因为正常求期望是加权和，什么叫加权和
这个就叫加权和。
每个样本出现概率不⼀样，概率⼤的乘起来就⼤，这个就产⽣偏重了（有偏估计）。
但是，但是我们不知道某个样本出现的概率啊。⽐如你从别⼈⼝袋⾥⾯随机拿了3张钞票。两张是⼗块钱，⼀张100元，然后你想估计下他⼝袋⾥的剩下的钱平均下来每张多少钱（估计平均值）。
然后呢？
⽆偏估计计算数学期望就是认为所有样本出现概率⼀样⼤，没有看不起哪个样本。
回到求钱的平均值的问题。⽆偏估计我们认为每张钞票出现概率都是1/2（因为只出现了10和100这两种情况，所以是1/2。如果是出现1 10 100三种情况，每种情况概率则是1/3。
哪怕拿到了两张⼗块钱，我还是认为⼗块钱出现的概率和100元的概率⼀样。不偏⼼。所以⽆偏估计，所估计的别⼈⼝袋每张钱的数学期望（平均值）= 10 ∗ 1/2 + 100 ∗ 1/2。
有偏估计那就是偏重那些出现次数多的样本。认为样本的概率是不⼀样的。
我出现了两次⼗块钱，那么我认为⼗块钱的概率是2/3，100块钱概率只有1/3. 有偏所估计的别⼈⼝袋每张钱的数学期望（平均值）= 10 ∗ 2/3 + 100 ∗ 1/3。
3.为何要⽤⽆偏估计？
因为现实⽣活中我不知道某个样本出现的概率啊，就像骰⼦，我不知道他是不是加过⽔银。
所以我们暂时按照每种情况出现概率⼀样来算。
GBDT原理深入刨析
想要理解GBDT的真正意义，那就必须理解GBDT中的Gradient Boosting（梯度提升） 和Decision Tree分别是什么？
梯度概念复习
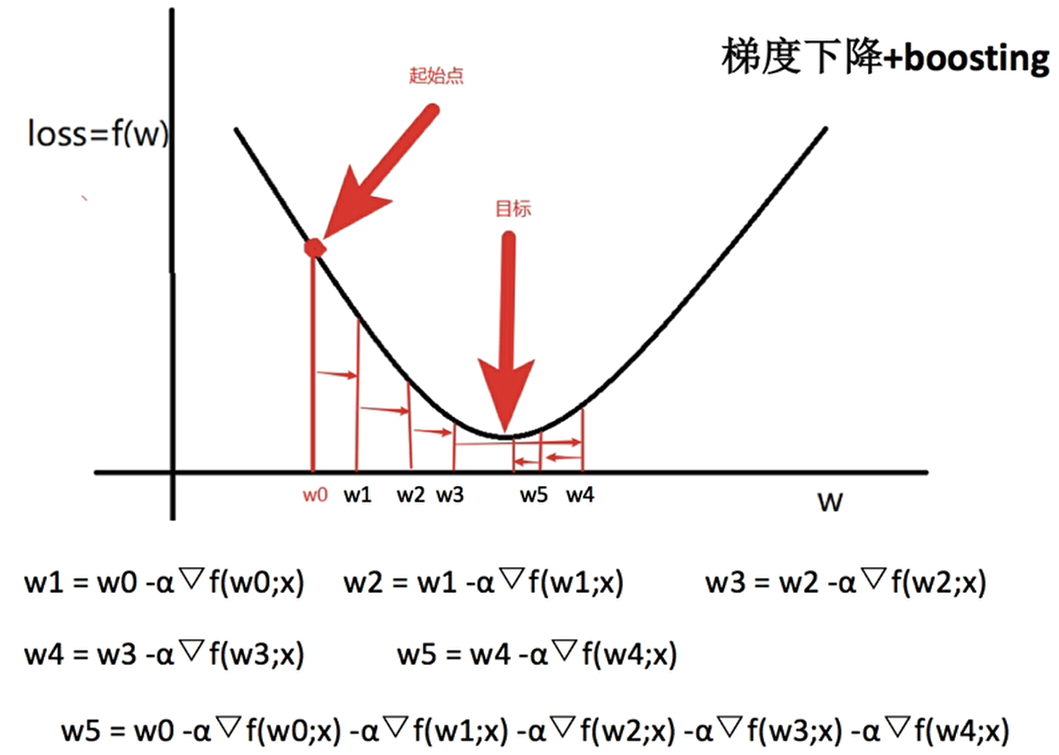
GDBT执行流程：
1 Decision Tree：CART回归树
⾸先，GBDT使⽤的决策树是CART回归树，⽆论是处理回归问题还是⼆分类以及多分类，GBDT使⽤的决策树通通都是CART回归树。
- 为什么不⽤CART分类树呢？
- 因为GBDT每次迭代要拟合的是梯度值，是连续值所以要⽤回归树。
对于回归树算法来说最重要的是寻找最佳的划分点，那么回归树中的可划分点包含了所有特征的所有可取的值。
在分类树中最佳划分点的判别标准是熵或者基尼系数，都是⽤纯度来衡量的，但是在回归树中的样本标签是连续数值，所以再使⽤熵之类的指标不再合适，取而代之的是平方误差，它能很好的评判拟合程度。
1.1 回归树生成算法（复习）
参照上文《回归决策树》
2 Gradient Boosting： 拟合负梯度
梯度提升树（Grandient Boosting）是提升树（Boosting Tree）的⼀种改进算法，所以在讲梯度提升树之前先来说⼀下提升树。
先来个通俗理解：假如有个⼈30岁，我们⾸先⽤20岁去拟合，发现损失有10岁，这时我们⽤6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们⽤3岁拟合剩下的差距，差距就只有⼀岁了。如果我们的迭代轮数还没有完，可以继续迭代下⾯，每⼀轮迭代，拟合的岁数误差都会减⼩。最后将每次拟合的岁数加起来便是模型输出的结果。
提升树算法：
（1）初始化f0(x) = 0
（2）对m=1,2,...,M
- （a）计算残差
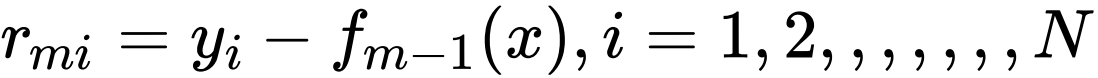
- （b）拟合残差rmi 学习⼀个回归树，得到hm(x)
- （c）更新
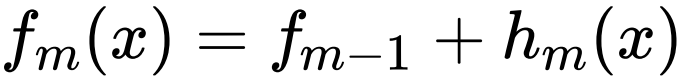
（3）得到回归问题提升树 
上⾯伪代码中的残差是什么？
在提升树算法中，
- 假设我们前⼀轮迭代得到的强学习器是：
- 损失函数是：
- 我们本轮迭代的⽬标是找到⼀个弱学习器：ht(x)
- 让本轮的损失最⼩化：
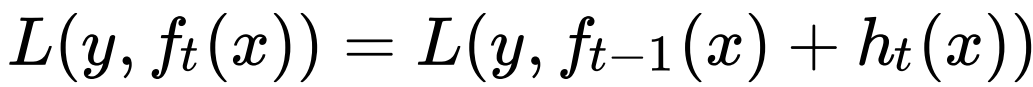
- 当采⽤平⽅损失函数时：
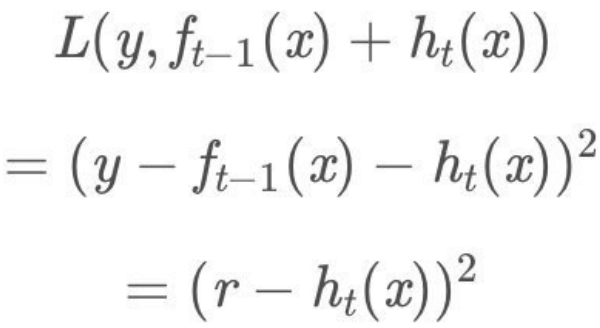
- 这⾥，
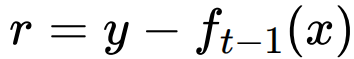是当前模型拟合数据的残差（residual）。 - 所以，对于提升树来说只需要简单地拟合当前模型的残差。
回到我们上⾯讲的那个通俗易懂的例⼦中，第⼀次迭代的残差是10岁，第⼆ 次残差4岁,,,,,,
当损失函数是平⽅损失和指数损失函数时，梯度提升树每⼀步优化是很简单的，但是对于⼀般损失函数⽽⾔，往往每⼀步优化起来不那么容易。
针对这⼀问题，Friedman提出了梯度提升树算法，这是利⽤最速下降的近似⽅法，其关键是利⽤损失函数的负梯度作为提升树算法中的残差的近似值。
那么负梯度⻓什么样呢？
- 第t轮的第i个样本的损失函数的负梯度为：
- 此时不同的损失函数将会得到不同的负梯度，如果选择平⽅损失：
- 负梯度为：
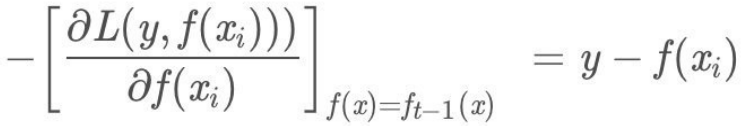
此时我们发现GBDT的负梯度就是残差，所以说对于回归问题，我们要拟合的就是残差。
那么对于分类问题呢？
- ⼆分类和多分类的损失函数都是logloss。
本⽂以回归问题为例进⾏讲解。
3 GBDT算法原理
上⾯两节分别将Decision Tree和Gradient Boosting介绍完了，下⾯将这两部分组合在⼀起就是我们的GBDT了。
GBDT算法：
- （1）初始化弱学习器
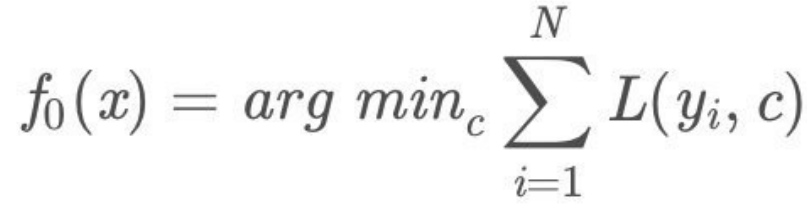
- （2）对m=1,2,...,M有：
- （a）对每个样本i=1,2,...,N，计算负梯度，即残差
-
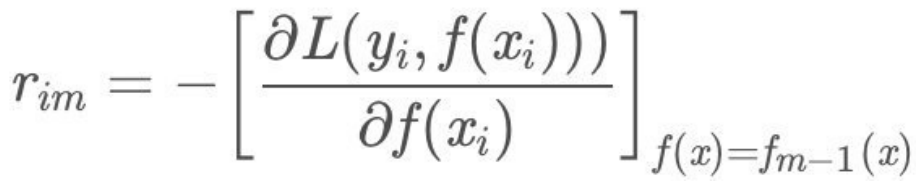
- （b）将上步得到的残差作为样本新的真实值，并将数据(xi, rim),i = 1, 2, ..N作为下棵树的训练数据，得到⼀颗新的回归树fm(x)其对应的叶⼦节点区域为Rjm, j = 1, 2, ..., J。其中J为回归树t的叶⼦节点的个数。
- （c）对叶⼦区域j=1,2,..J计算最佳拟合值
-
- （d）更新强学习器
- （3）得到最终学习器
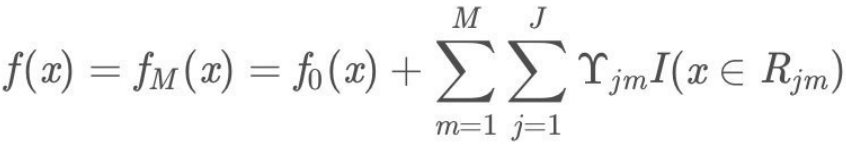
4 实例介绍
4.1 数据介绍
根据如下数据，预测最后⼀个样本的身⾼。
| 编号 | 年龄 (岁) | 体重（kg） | 身高 (m)(标签值) |
|---|---|---|---|
| 0 | 5 | 20 | 1.1 |
| 1 | 7 | 30 | 1.3 |
| 2 | 21 | 70 | 1.7 |
| 3 | 30 | 60 | 1.8 |
| 4 (要预测的) | 25 | 65 | ? |
4.2 模型训练
4.2.1 设置参数：
- 学习率：learning_rate=0.1
- 迭代次数：n_trees=5
- 树的深度：max_depth=3
4.2.2 开始训练
计算损失函数，求出第一个预测值：
思路：
1.初始化弱学习器:
损失函数为平⽅损失，因为平⽅损失函数是⼀个凸函数，直接求导：
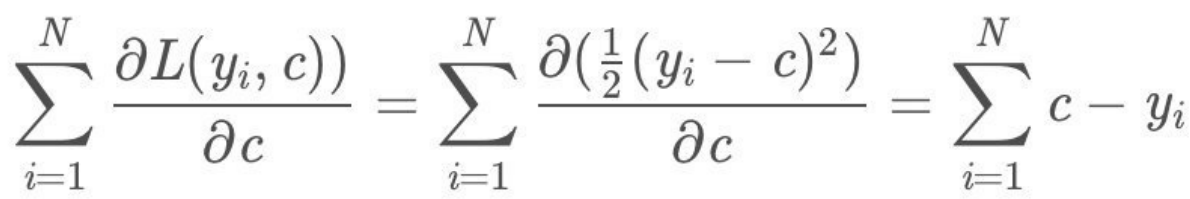
令导数等于0，得到c。
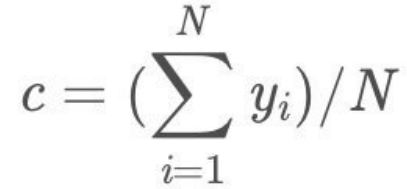
具体实现：
所以初始化时，c取值为所有训练样本标签值的均值。c = (1.1 + 1.3 + 1.7 + 1.8)/4 = 1.475，此时得到初始学习器f0(x)：
f 0(x) = c = 1.475
2.求解划分点
计算负梯度，根据上⽂损失函数为平⽅损失时，负梯度就是残差，再直⽩⼀点就是 y与上⼀轮得到的学习器f m-1的差值：
残差在下表列出：
| 编号 | 真实值 | 残差 | |
|---|---|---|---|
| 0 | 1.1 | 1.475 | -0.375 |
| 1 | 1.3 | 1.475 | -0.175 |
| 2 | 1.7 | 1.475 | 0.225 |
| 3 | 1.8 | 1.475 | 0.325 |
重构目标值
此时将残差作为样本的目标值来训练弱学习器f 1(x)，即下表数据
| 编号 | 年龄 (岁) | 体重（kg） | 标签值 |
|---|---|---|---|
| 0 | 5 | 20 | -0.375 |
| 1 | 7 | 30 | -0.175 |
| 2 | 21 | 70 | 0.225 |
| 3 | 30 | 60 | 0.325 |
接着，寻找回归树的最佳划分节点，遍历每个特征的每个可能取值。
从年龄特征的5开始，到体重特征的70结束，分别计算分裂后两组数据的平⽅损失（Square Error），
SE l 左节点平⽅损失，SE r 右节点平⽅损失，找到使平⽅损失和SE sum = SE l + SE r 最⼩的那个划分节点，即为最佳划分节点。
例如：以年龄21为划分节点，将⼩于21的样本划分为到左节点，⼤于等于21的样本划分为右节点。左节点包括x 0 , x 1，右节点包括样本x 2, x 3
注意！下面的的0.275是每个划分类的标签值的均值
SE l = [−0.375 − (−0.275)] 2+ [−0.175 − (−0.275)] 2= 0.02 解释：-0.275=（-0.375-0.175）/2
SE r = [0.225 − 0.275] 2+ [0.325 − 0.275] 2= 0.005 解释：-0.275=（0.225+0.325）/2
SE sum = 0.025,
所有可能划分情况如下表所示：
|
划分点 |
⼩于划分点的样本 |
⼤于等于划分点的样本 |
SE l | SE r | SE sum |
| 年龄 5 | / | 0，1，2，3 | 0 | 0.327 | 0.327 |
| 年龄 7 | 0 | 1，2，3 | 0 | 0.14 | 0.14 |
| 年龄 21 | 0，1 | 2，3 | 0.02 | 0.005 | 0.025 |
| 年龄 30 | 0，1，2 | 3 | 0.187 | 0 | 0.187 |
| 体重 20 | / | 0，1，2，3 | 0 | 0.327 | 0.327 |
| 体重 30 | 0 | 1，2，3 | 0 | 0.14 | 0.14 |
| 体重 60 | 0，1 | 2，3 | 0.02 | 0.005 | 0.025 |
| 体重 70 | 0，1，3 | 2 | 0.26 | 0 | 0.26 |
以上划分点是的总平⽅损失最⼩为0.025有两个划分点：年龄21和体重60，所以随机选⼀个作为划分点，这⾥我们选 年龄21 现在我们的第⼀棵树⻓这个样⼦：
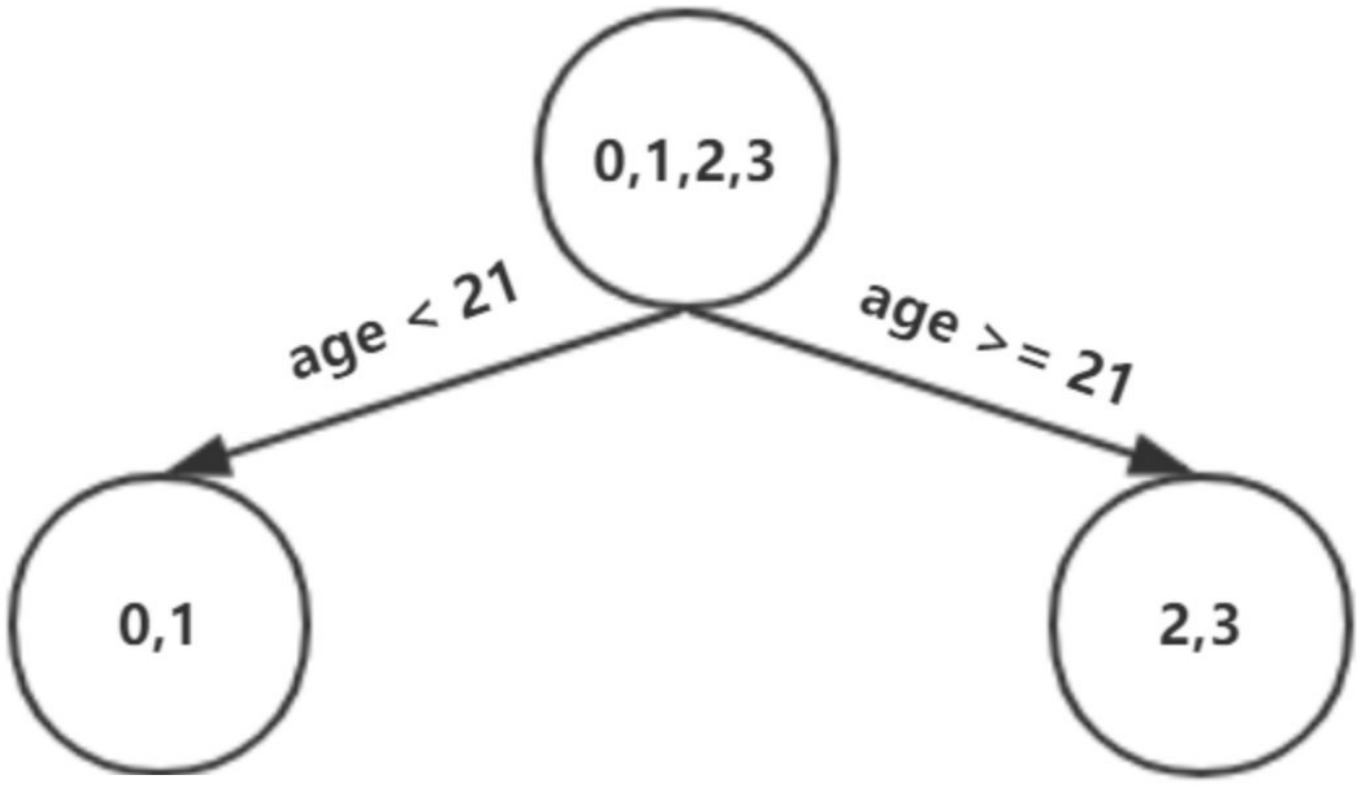
我们设置的参数中树的深度max_depth=3，现在树的深度只有2，需要再进⾏⼀次划分，这次划分要对左右两个节点分别进⾏划分：
对于左节点，只含有0,1两个样本，根据下表我们选择年龄7划分
| 划分点 | 小于划分点的样本 | 大于等于划分点的样本 | |||
|---|---|---|---|---|---|
| 年龄 5 | / | 0, 1 | 0 | 0.02 | 0.02 |
| 年龄 7 | 0 | 1 | 0 | 0 | 0 |
| 体重 20 | / | 0, 1 | 0 | 0.02 | 0.02 |
| 体重 30 | 0 | 1 | 0 | 0 | 0 |
对于右节点，只含有2,3两个样本，根据下表我们选择年龄30划分（也可以选体重70）
| 划分点 | 小于划分点的样本 | 大于等于划分点的样本 | |||
|---|---|---|---|---|---|
| 年龄 21 | / | 2，3 | 0 | 0.005 | 0.005 |
| 年龄 30 | 2 | 3 | 0 | 0 | 0 |
| 体重 60 | / | 2，3 | 0 | 0.005 | 0.005 |
| 体重 70 | 3 | 2 | 0 | 0 | 0 |
现在我们的第⼀棵树⻓这个样⼦：
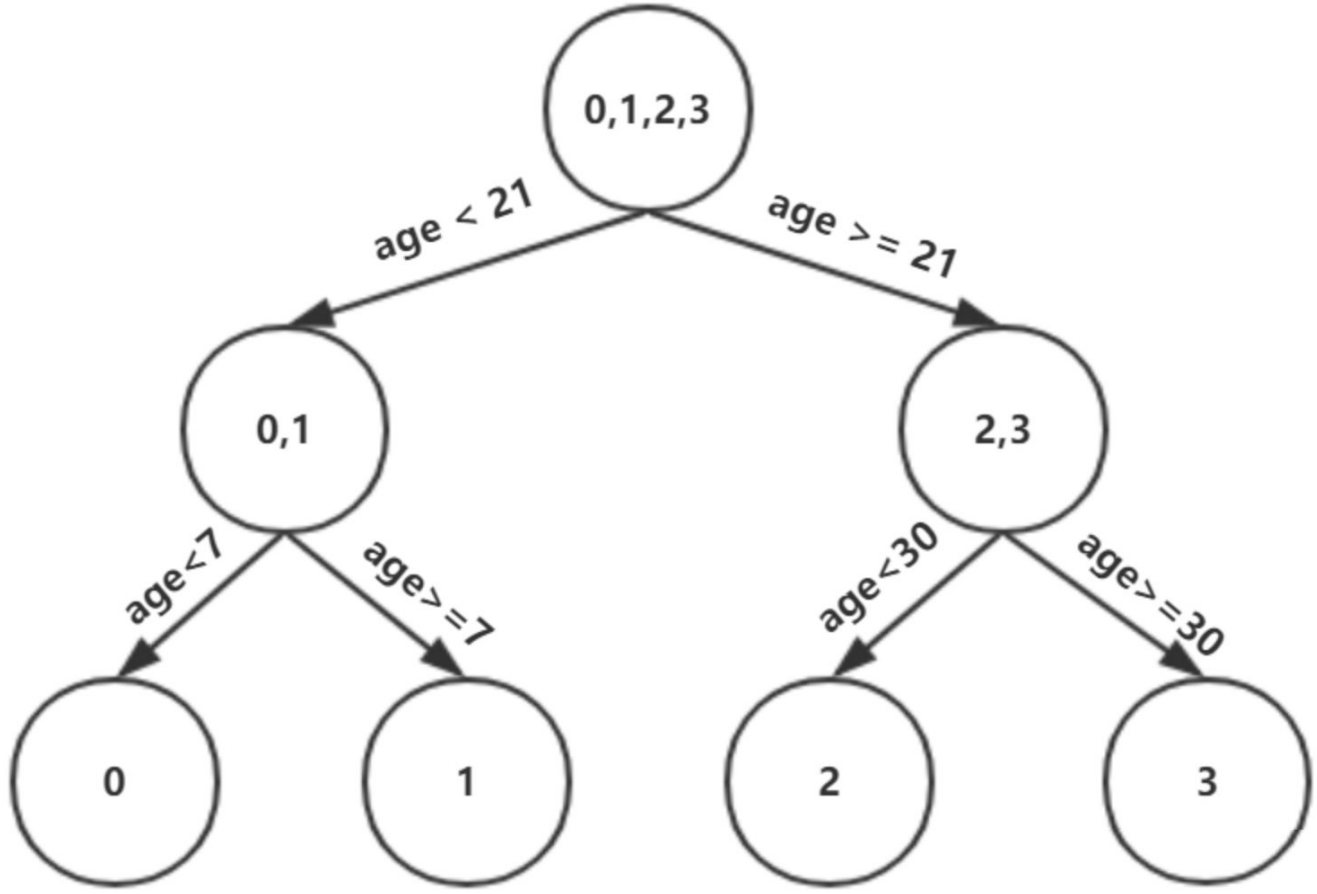
此时我们的树深度满⾜了设置，还需要做⼀件事情，给这每个叶⼦节点分别赋⼀个参数Υ，来拟合残差。
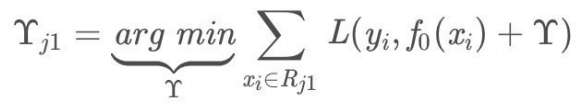
这⾥其实和上⾯初始化学习器是⼀个道理，平⽅损失，求导，令导数等于零，化简之后得到每个叶⼦节点的参数Υ，其实就是标签值的均值。这个地⽅的标签值不是原始的 y，⽽是本轮要拟合的标残差 y − f (x).
根据上述划分结果，为了⽅便表示，规定从左到右为第1,2,3,4个叶⼦结点
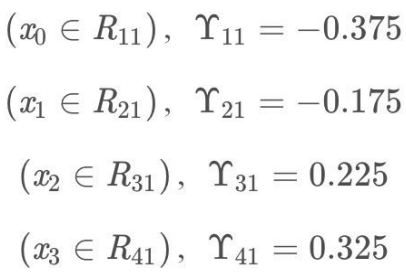
此时的树⻓这个样⼦：
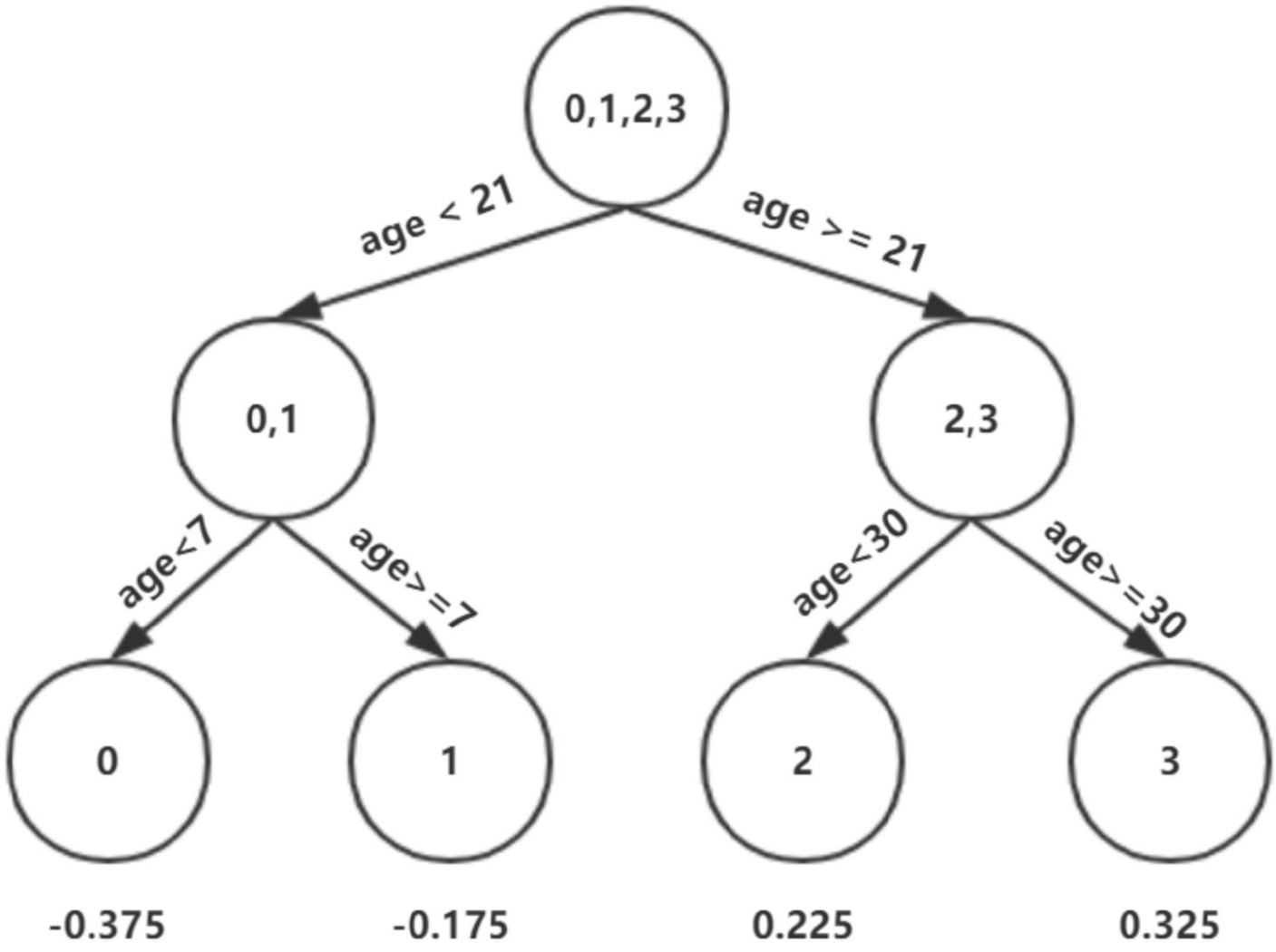
此时可更新强学习器，需要⽤到参数学习率：learning_rate=0.1，⽤lr 表示。
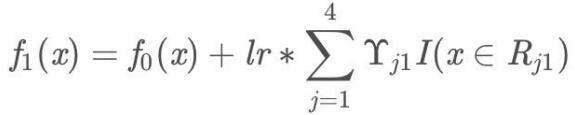
为什么要⽤学习率呢？这是Shrinkage的思想，如果每次都全部加上（学习率为1）很容易⼀步学到位导致过拟合。重复此步骤，直到 m>5 结束，最后⽣成5棵树。
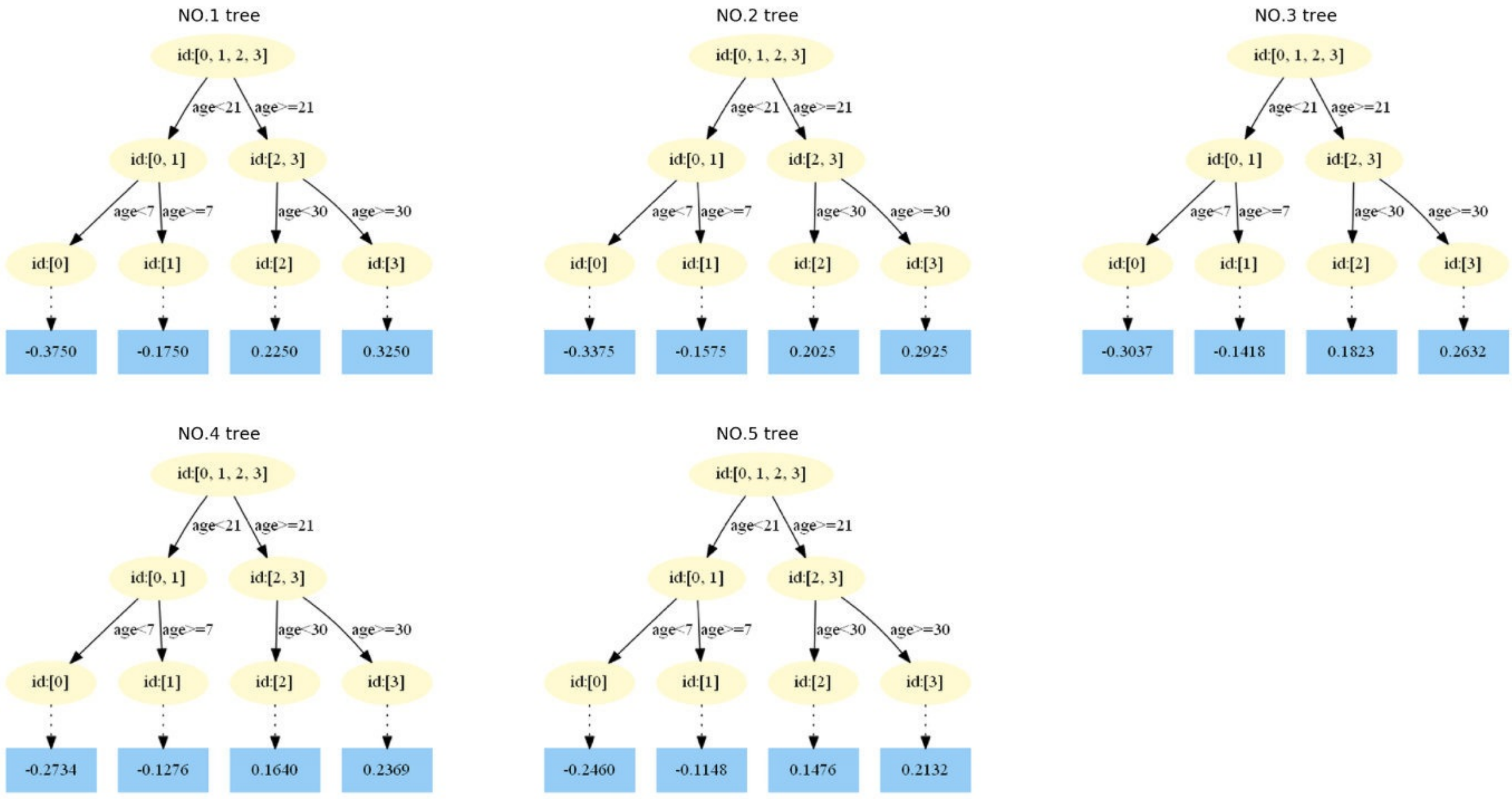
结果中，0.9倍这个现象，和其学习率有关。这是因为数据简单每棵树⻓得⼀样，导致每⼀颗树的拟合效果⼀样，⽽每棵树都只学上⼀棵树残差的0.1倍，导致这颗树只能拟合剩余0.9了。
3.得到最后的强学习器
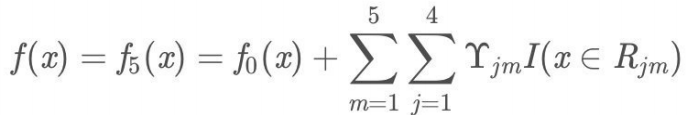
4.预测样本：
f0(x) = 1.475
- 在f1(x)中，样本4的年龄为25，⼤于划分节点21岁，⼜⼩于30岁，所以被预测为0.2250;
- 在f2(x)中，样本4的…此处省略…所以被预测为0.2025;
- 在f3(x)中，样本4的…此处省略…所以被预测为0.1823;
- 在f4(x)中，样本4的…此处省略…所以被预测为0.1640;
- 在f5(x)中，样本4的…此处省略…所以被预测为0.1476.
最终预测结果：
f(x) = 1.475 + 0.1 ∗ (0.225 + 0.2025 + 0.1823 + 0.164 + 0.1476) = 1.56714
5 ⼩结
GBDT算法原理【知道】
- （1）初始化弱学习器
- （2）对m=1,2,...,M有：
- （a）对每个样本i=1,2,...,N，计算负梯度，即残差
-
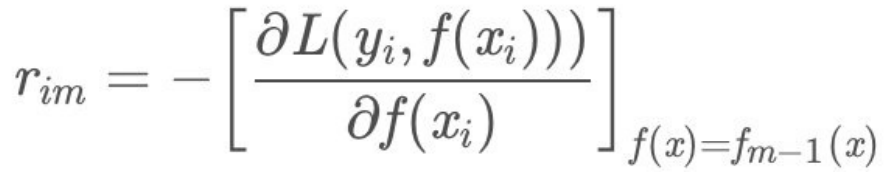
- （b）将上步得到的残差作为样本新的真实值，并将数据(xi, rim),i = 1, 2, ..N作为下棵树的训练数据，得到⼀颗新的回归树fm(x)其对应的叶⼦节点区域为Rjm, j = 1, 2, ..., J。其中J为回归树t的叶⼦节点的个数。
- （c）对叶⼦区域j=1,2,..J计算最佳拟合值
-
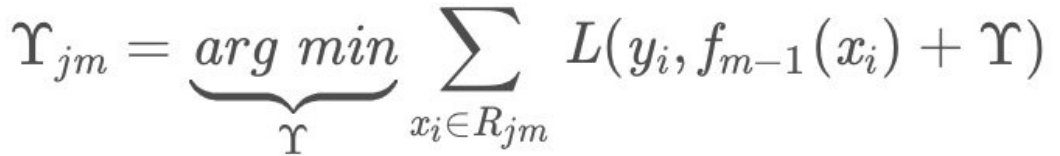
- （d）更新强学习器
- （3）得到最终学习器
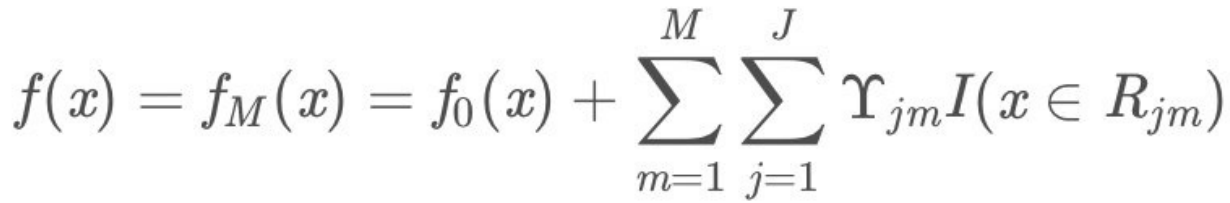
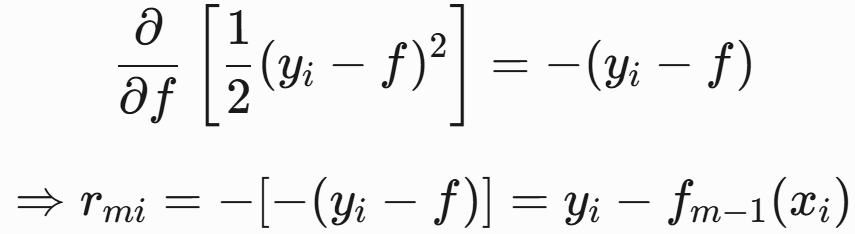
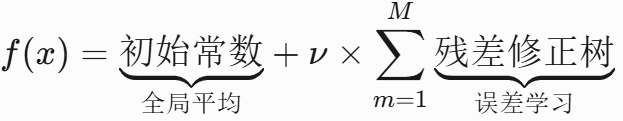
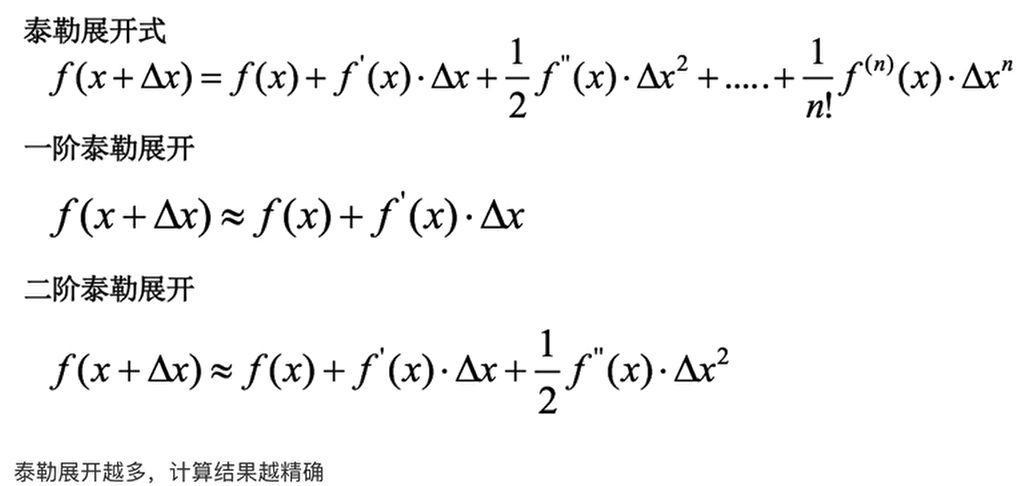
浙公网安备 33010602011771号