特征值与代表元计数

特征值与代表元计数

如果是有多个方案，算作一种本质不同方案，那么直接计数所有方案就会重复，这时我们只找满足某个条件的，叫做一个本质不同方案的”代表元“。

如果每个方案都要计数一次，我们需要找一个状态 \(s\) ，使得一个方案 \(F\) 只属于一个 \(s\)。这样对 \(s\) 计数就是对 \(F\) 计数。如果这个 \(s\) 恰为 \(F\) 中的某个部分，我们称这个部分为 \(F\) 的特征值。

代表元计数——CF720D Slalom 题解

首先这题路径数的定义与平时不太一样：如果其没有以不同的方式跨过障碍，即使路径所走的是不同的，也要算作一条。

对于算作一条的许多路径，如果可以使仅其中一条产生贡献，便可以解决问题。为了方便，这里取最低的一条，称作代表路径

设 \(f_{i,j}\) 表示走到 \(i,j\) 的代表路径数是多少。

如果没有矩形，直接 \(f_{i,j}=f_{i-1,j}\)。

如果有矩形，形如下图。

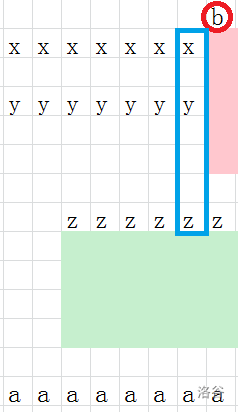
设向下第一个碰到的第一个矩形上界为 \(u\) 那么 \(f_{i,j}=\sum_{k=u+1}^jf_{i-1,k}\)

从左到右扫描线，求和用线段树，找 \(u\) 用 set 维护一下当前被覆盖的线段。复杂度 \(T:\mathcal O((m+k)\log n) M:\mathcal O(k)\)。

找唯一特征值去重转移DP——CF1210F2 Marek and Matching

匹配肯定利用霍尔定理，先写出：\(\forall S,|S|-|G(S)|\le 0\)。

图论计数往往考虑容斥，设 \(f_{S,T}\) 表示对于二分图 \((S,T)\)，出现大小为 \(|S|\) 的匹配的概率，首先是 \(mat(S,T)\) 表示 \(G(S)\ge S\) 的方案数。然后想怎么减去，考虑怎么用一个信息代表一类不合法的情况。

这里考虑找出使得 \(|S|-|G(S)|\) 最大 \(S\) 来代表，若有多个则取 \(|S|\) 最小的，可以证明对于任意的无完美匹配的图， \(S\) 是唯一的，于是这样就用 \((S,T=G(S))\) 代表了一类无完美匹配的图，设方案数为 \(g_{S,T}\)。这里 \((S,T)\) 就是一个不合法图的“特征值”。

设 \(N(S,T)\) 表示 \(S,T\) 之间没有边的概率。

根据意义得到转移：

\[f_{S,T}=mat(S,T)-\sum_{S'\subseteq S,T'\subseteq T,S'\ne \emptyset}g_{S',T'}f_{S\setminus S',T\setminus T'}N(S',T\setminus T') \]

然后考虑转移 \(g_{S,T}\)，根据意义我们要求 \((S,T)\) 是二分图 \((S,T)\) 的特征值，所以 \(G(S)=T\)，设 \(smat(S,T)\) 为 \(mat(S,T)\) 的所有情况中 \(G(S)=T\) 的。

\[g_{S,T}=smat(S,T)-\sum_{S'\subseteq S,T'\subseteq T,S'\ne S,|S'|-|T'|\ge |S|-|T|}g_{S',T'}h_{S\setminus S',T\setminus T'}N(S',T\setminus T') \]

为了满足 \(G(S)=T\) 这里 \(h_{S,T}\) 表示 \(f_{S,T}\) 中所有满足 \(G(S)=T\) 的。于是得到 \(h\) 的转移式：

\[h_{S,T}=smat(S,T)-\sum_{S'\subseteq S,T'\subseteq T,S'\ne \emptyset}g_{S',T'}h_{S\setminus S',T\setminus T'}N(S',T\setminus T') \]

发现 \(h_{U,U}\) 也为答案，所以没必要使用 \(f\) 了。

最后：

\[smat(S,T)=\sum_{T'\subseteq T}(-1)^{|T'|}N(S,T') \]