Kruskal 重构树学习笔记

Kruskal 重构树学习笔记

在Kruskal的过程中同时维护Kruskal重构树，每加入一条边，建立一个新点，新点点权为原来的边权，其左右儿子就是连接的两个连通块根。

这样新建出的树，满足原树中两点路径之间最大值就是Kruskal重构树上两点的LCA，实现了从最值到确定值的转变。

所以常常由于求解“最小瓶颈路”问题。

这也告诉我们，在原图上不好求解信息时，可以考虑直接改变原图。

类似的有：圆方树、缩点、最小割树、点分树、全局平衡二叉树，都有各自的功能。

例题：CF2021E3 Digital Village (Extreme Version) - 洛谷

P9984 [USACO23DEC] A Graph Problem P - 洛谷

这道题的技巧是，把信息放在另一边。

可以发现一定是通过最小生成树上的边扩展，可以想到Kruskal。建出Kruskal重构树方便思考，发现每次合并两个连通块时，一定是先走完一个连通块，再走这条边，再从另一个连通块的某个点开始遍历另一个连通块。

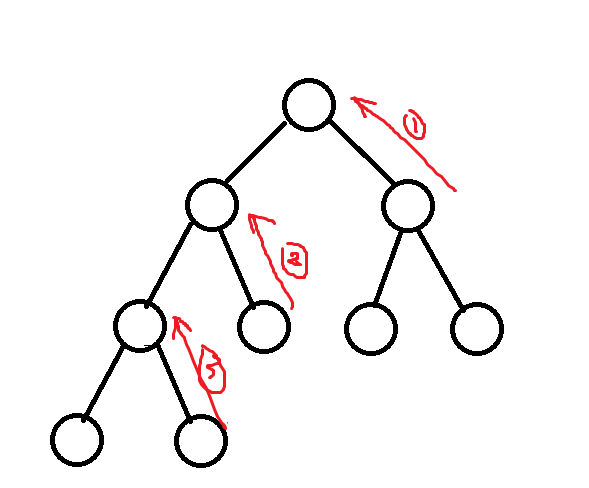
可以我们把”走这条边+从另一个连通块的某个点开始遍历另一个连通块“的值看作一号边的边权，那么最终答案就是到根路径的权值合并。

于是现在的问题是如何实时求出这个权值，尤其是”从另一个连通块的某个点（设作 \(x\) ）开始遍历另一个连通块“的值。可以发现这相当于是合并前的”答案“，即此时 \(x\) 到其当前根的路径权值合并，注意到树是不断合并的，可以使用路径权值压缩的并查集。

最终复杂度 \(\mathcal O(m\log m)\)。