dash
2025.8.18
一套题,未完成
2025.8.19
2129E. Induced Subgraph Queries
可以算是独立相出。但是有两个不顺利的地方
- 想了很多错误的方向,可以说是枚举了各种可能的方法组合。
- 卡了许久的常数,开始是因为数据结构没使用好,后来最有用的是去掉define int long long,这个确乎是会影响时间的。
- 这道题最关键的一个点是在调整原先的莫队,并且同时进行两个莫队,且由于坐标之间的关联,复杂度是根号
Submission #334485483 - Codeforces
2128E2. Submedians (Hard Version)
唯一需要想到合法的答案构成区间。
考虑的方法是邻域调整,即不是考虑任意两个区间关系,而是考虑一个最微小的变化,以及这个微小变化带来的影响,这样就简单多了。
Submission #334501846 - Codeforces
有两点没想出来看了Hint1,2
-
如果我直接对整个图考虑是非常难的,因为一个“图”是一个极其庞大且抽象的对象,所以正确的做法是,根据定义,假设答案存在,找到原题真正关心的东西。整体考虑图的染色情况,就是我无法下手的原因。
比如本题,真正关心的是某一条不经过k的最短路径,并且为了分析,我应该找到具体的某一个,而不是仅仅知道“存在”。
-
条件的放宽。当限制条件是对于所有元素满足某某性质,那这个性质不一定是真正的严格限制。类似于:
真正的限制:\(\forall x,A(x)\) 成立,而我可以找的是 \(\forall x,B(x)\) 成立,且 \(B(x)\) 是 \(A(x)\) 的一个必要条件。
单看某个条件是不对的,但是合起来就对了。之前讨论过这种转换,但要在实战中打出还是很难的,需要先猜后证?
由于这种转化的本质是让条件变得好看,所以我可以往一些比较好看的 \(A(x)\) 的必要条件上猜,且不要轻易否定一个结论。
这让我想起另一类相似的转化:求 \(\max_x A(x)\),转换为求 \(\max_x B(x)\),同样满足 \(B(x)\) 是 \(A(x)\) 的充要条件,当时当 \(B(x)\) 不满足时,一定不会变成答案。比如NOIP2024T4。
Submission #334526366 - Codeforces
2025.8.20
看了完整题解,原因是没思路+读错题,两点:
- 状压做图论计数时,一般会有 \(f,g\) 分别表示图/联通子图方案树,并且根据题目对图的额外限制,可以增加很多新的维度
- 神奇的环限制,考虑树图转换,分开研究树边/非树边的性质
Submission #334621771 - Codeforces

算是自己做出来的,有个难点,就是要注意到前 \(n-1\) 个格子等价,然后用所有各自的贡献之和除以 \(n-1\) 算出单个格子的贡献,这个直接推式子比较难,整体用意义做更简单。
Submission #334638009 - Codeforces

关键问题在于:
-
没想到值域<=n,以此来限制合法对(i,j)的个数
-
虽然权值改变很复杂u,但是只要找到第一个k,整个计算就与 a_j无关了,、可以预处理,而不是向我一样重新算
Submission #334665352 - Codeforces

2025.8.21
原思路还是会算重,因为把结构套的太复杂了。用以下技巧可以简化:
- 按照易于处理的方式安排枚举顺序,或者枚举其中计算得到的某些变量。
- 去重的时候找到一个”重复点“,使得重复的成因与其他地方操作无关,这样就可以用乘法乘起来,比如本题处理了一个 \(h[j][i]\),表示出现了先大后小的两个同位循环位移,这与 \(j\) 之前的无关,所以可以之间将 \(f_i\) 减去 \(f_{j-1}\times h[j][i]\) 来去重。
- 先算离线转移贡献,再转移。在转移 \(f_{i}=\sum_{j<i}f_jVal(j+1,i)\) 中,\(Val(j+1,i)\) 单次计算为 \(O(n)\),但是将 \(i-j\) 相同的 \(Val(j+1,i)\) 一起计算,可以实现均摊 \(\mathcal O(1)\),所以应该先离线算 \(Val\) 再转移 \(f\)。
Submission #334739496 - Codeforces

G. Eulerian Line Graph花了5个小时,失败了,我证明不了题解的结论。以后选题不要选Down了一堆的比赛里的题。这道题的各种结论感觉很大程度上是手玩而非证明。也有启发就是要有目的性的进行手玩,并不断总结,不要盲目手玩。
-
DP的时候很巧妙,没有对转化后的式子进行DP,而是DP了原式,存 \(\sum a\),作为状态反而更加简单粗暴。
-
并且这里使用动态位置也可以减少状态,即动态插到当前维护的数组的左右两边,而非实际插在数组的某个位置。
还算可以的区间DP,设计DP得先找性质,再根据性质设计DP,什么性质都没有,就只能枚举,是不能DP的。
Submission #334971639 - Codeforces

2025.8.22
还是说先分析性质,才能设计DP,列出转移式再优化转移。
Submission #334975990 - Codeforces

-
想到在变化的时候什么不变,然后不断地修正+补充,最后得到答案。
-
还有就是学习xorShift算法,乱搞的一个随机函数被卡了
-
我忘记了最小表示法,最小表示法的求解是需要一定分析的串串理论,值得反复温习。
Submission #335006085 - Codeforces

D. Gellyfish and Forget-Me-Not
-
对于choose A or B 的问题,可以先假设 choose A,然后再判断是否 choose \(B-A\) 即变化量。
-
有个与线性基相关的性质,由于不论前面的数怎么选,总是后面的数可以基于前面的数做决定,比如对于两个数 \(x,y\),他和 \(x\oplus y,y\) 这样一对数是等价的。
从线性基的角度解释,根据博弈论理论,一个数的决策仅与后面的数和自身进入时的初始状态有关,然而当前这个数异或上后面的某个数后,其构成的张成空间没有改变。所以原来能达成的方案,再异或上后面的数后,可以通过调整后面的数的决策,达到相同的等价情况。
Submission #335034206 - Codeforces

怎敢想?维护可行集合的 \(\Delta\)。然后势能分析。看起来暴力其实就对了。
Submission #335102445 - Codeforces

2025.8.24
大小关系->01序列
Submission #335293726 - Codeforces

第一周总结
AC14题(CF2800 4题,CF2600 3题,CF3100,CF3200 各2题,CF2900,CF3000,洛谷紫题 各1题),放弃1题。
2025.8.25
AT_codefestival_2016_final_i Reverse Grid - 洛谷
- 每一行和每一列作为一个点,以交叉处的信息建边
- 如果一次操作的影响太大,可以看对于每一个影响是怎样的
开始时间:16:20,AC时间19:00,其中18:00-18:45在吃饭。
Submission #68805524 - CODE FESTIVAL 2016 Final
2025.8.26
开始时间2025.8.25 19:03,22:35走了,WA on test 5,第二天7:34开始,10:48结束.开始大约1.5个小时读错题了。
- 洪泛法好
- 最小割转最短路:
- 平面图最小割=对偶图最短路
- 网格图最小割=另一个方向的最短路
Submission #335536966 - Codeforces

显然可以直接用DP求出执行操作2的最小次数。但是记录方案的代码十分复杂。
考虑到,出现非链的情况,至少需要4个点,于是我们直接尝试构造链。然后将点按照链端,链中间,非链染色。
经过一些讨论,但无论如何,使用操作2,就一定有另外三个点,那么操作2就是 \(\lfloor\frac n4\rfloor\) 次的。
Submission #335538726 - Codeforces

开始于14:24,AC于16:37
如果要打表
我们一直说打表,打什么内容是十分关键的,这又取决于我们关注什么。
这个题的操作十分复杂,所以我们应该先关注什么样的序列是可以得到的,而非直接关注答案是怎样的。
将整个打表内容排序,也是非常好的方法。
在完全不知道结果前,从什么角度看打表内容也十分关键。更重要的是不要当作“偶然”。
所以还是要积累一点常见的角度。
打表对象:什么样的序列能生成
打表方法:排序
观察角度:如果一个生成,他所有的“子集”也可以生成.这里的"子集"是某种角度下的可重集.
如果要分析
这个结论也能分析出来,关键在于要考虑一个合法的结果是可以怎样生成的。
考虑如果“我要让一个位置的值为 \(v\)”,那么应该怎样操作,这是就不要考虑其他的位置了。
Submission #335569148 - Codeforces

开始于 16:40,18:04吃饭,18:57回来,20:22AC
自己做出,比较平凡。
Submission #335600668 - Codeforces

2025.8.27
8:37开始,10:44AC
自己做出,比较平凡。
Submission #335742933 - Codeforces

Problem - 2092F - Codeforces
10;50开始,12:14去吃饭,14:12回来16:53AC
- 什么时候该换个思路呢?至少不应该吊死在一棵树上
- 在数据范围极大时(1e7级别),把vector换成邻接表可以大力卡常
- 优化空间复杂度也需要分析性质。
Submission #335776129 - Codeforces

17:06开始,18:06去吃饭,18:55回来,20:22AC
- 换掉vector,常数就除2
- 在处理“排除本集合元素的最大值“时,可以直接用
pair<int,int>维护最大值,和另一个所在集合不同的次大值,而不是用值域线段树,麻烦还多 \(\log\)。
Submission #335805004 - Codeforces

2025.8.28
巡逻网络 (net)
- \(|a-b|=\max(a-b,b-a)\),于是在求最大值时,不需要考虑相对大小,只需要保证最后取到那么多个 \(-\),那么多个 \(+\) 。在最优化问题中把绝对值化为最值。
- 减少循环个数可以卡常,这是因为减少了jump的次数,而jump是不连续访问,十分耗时
【USsR #1】彩色括号 - 题目 - Universal Online Judge
- 把变量设出来,形式化列式,在这过程中,需要考虑大量情况,并用一些变量表示
- 线性规划之类,最优值一定取在某条线,或某个点上,证明考虑移动最优值位置,类似单纯形法(把算法忘了,需要复习)。这样即使暴力,也可以联立求解某条线,某个点,缩小答案空间。这往往要画函数图像。
提交记录 #789136 - Universal Online Judge
2025.8.29
符文石
图上整体二分,每次二分出一个贡献集合 \(S\) 与待更新集合 \(T\),每次 Check 如果要从 \(S\) 走到 \(T\),则为 \(O(n)\),TLE。正确做法将 \(S\) 上的点挂在 \(T\) 上(每次二分集合时进行),这样复杂度为 \(O(|S|+|T|)\) 复杂度正确。并且结合性质分析复杂度。
小 L 造数据
对于 \(x\bmod p\),在 \(q\) 进制下 \(x\bmod p\bmod \operatorname{lowbit}_q(p)=x\bmod \operatorname{lowbit}_q(p)\),即 \(x\bmod p\) 不影响 \(q\) 进制下 \(p\) 后面最低的几位为 \(0\) 的位的值,证明考虑把 \(\div\) 看作 \(-\) 可以证明。
跳到下一个大于 \(x+d\) 的白点,可以将白点 \(x\) 连到 \(x+d\),将黑点 \(x\) 连向 \(x+1\),这样一路上跳到的白点就是原问题了。一个建边技巧,即用非关键点建立结构,关键点产生贡献。
Submission #336199408 - Codeforces
第二周总结
1洛谷紫,1CF2500,2CF2800,3CF2900,1CF3000,2CF3100,1UOJ,3模拟赛题=14题
2025.9.1
模拟赛总结:挂大分,告诉我们过了样例 \(\implies score\in [0,100]\)。所以要对拍。
P11504 [NordicOI 2018] French Fries - 洛谷
首先除太多数太小,用打表得到一个范围,即\(\le 10^5\)。
然后就是用 double 存大数
于是有 \(74\) 分。
神奇误差分析。将 \(\frac {mx}{mn}<D=1.25\) 的修改全部变成 \(\sqrt{mx\times mn}\),然后误差分析就是对的。
由于单调,假设整体最大值为 \(MX\),最小非0值为 \(MN\),则有 \(\log_D{\frac{MX}{MN}}\) 段。由于 \(MX\le 1\),当 \(MN<10^{-10}\) 时就没用了,直接设作 \(0\),复杂度就是对的。
-
直接考虑最后停在哪个点。然后通过分析得到答案与最后停在哪个点的关系。抽象来说,直接考虑终点状态。
-
但是怎么到这个点,便要考虑过程。
-
精细实现,不然就会有很多情况,使得写的和想的不一样。
Submission #336492030 - Codeforces
P10644 [NordicOI 2022] 能源网格 Power Grid - 洛谷
非常高妙。
- 发现充要条件并转换,先找到必要条件(再显然也要找),然后证明其充分性,对于这种构造题,可以构造证明
- 若要满足多个条件,先假设满足一个条件,再用“调整法“调整至满足另外一个条件,并且在调整的过程中保证第一个条件一直满足。这也是一种 微小调整法。这样可以转化条件。
- bitset优化背包。
2025.9.2
模拟赛总结:T1想了太久(1.5h)导致没时间细想T2,结果本来就没有更优的解法了。如果一段时间想不出来就不要想了,有可能本身就是题目的问题。
因子操作
-
势能性:一个数只会减少,有不会低于某个下界,那么他的操作次数就有限了。
-
神奇复杂度的分析:以实际结果为准,比如此题的此算次数就是 \(\mathcal O(\sum_{i=1}^np_i\min\{\frac{n}{x},w\}^2)\),其中 \(p_i\) 就是最初的答案,这就需要先写出来用程序跑出 \(p_i\)。”小 L 造数据“一题的自由元个数,也要先设计出算法,然后跑出来得到,因为 xor shift 的 rand() 函数太随机了,难以分析。
-
如果只相当 \(x\) 小时 \(d(x)\) 也较小,采用“根号”分治,阈值为 \(D\):
- \(x\le D\) 时刻算出最优答案
- \(x>D\) 暴力向前跳。
不知道复杂度,但可以过。此方法David_Mercury有记载。
18:53开始19:14看题解20:01AC
线段树做法(性质做法)
首先考虑 \(j<i,a_j>a_i\),做完后将 \(a_i\) 取相反数再做一次即可。
我们有一种经典的扫描线的技巧,即扫描 \(r\) 用 \(b_i\) 表示 \([i,r]\) 的答案。最朴素的是扫描 \(r\) 时,直接向前做区间修改。
这道题,需要进一步的分析,也就是说,我们不能直接简单粗暴的用区间进行修改。
于是我们考虑怎样的修改是有效的,这里的有效包含两重意义:对 \(b_i\) 产生修改和对全局答案产生影响。
首先分析 \(i\to j\) 的条件,假设之前是 \(k\to j\),发现“ \(b_i\) 发生修改”当且仅当 \(a_k<a_i\)。然后就没有性质了。
一个技巧是考虑同时存在多个转移的条件,假设同时存在 \(i\to j,i\to k\) 的更新,这里设 \(k<j\)。于是 \(i\to j\) 的更新可能对 \(i\to k\) 的更新产生影响,首先若 \(a_k\ge a_j\) ,从“对全局答案产生影响”的角度则不会有转移 \(i\to k\)。
顺着这个思路,如果 \(j,k\) 之间的答案优于 \(i,k\) 之间的答案,那么 \(i\to k\) 也可以不存在,于是 \(i\to k\) 存在则要求 \(a_k-a_i<a_j-a_k\implies a_k-a_i<\frac12(a_j-a_i)\) 于是得到每多一个转移,值域减半,复杂度变为 \(\mathcal O(n\log^2 V)\)。
莫队做法(火箭毛毛虫做法)
直接用莫队,需要维护一个有序序列,和带删除的最大值,是 \(\mathcal O(n\sqrt m\log n)\) 的。
把莫队换成回滚莫队,只加不删,于是“带删除的最大值”就不用set了。考虑如何维护有序序列,并且支持查询前驱后继。
为了平衡掉 log,自然用值域分块,将贡献看作块内于块间。假设块长为 \(B\),那么块间的前驱后继直接维护最小值与最大值即可,维护后在每次询问时遍历所有块。
块内找后继暴力是 \(\mathcal O(B)\) 的,我们放到每次修改做。这样复杂度就是 \(\mathcal O(n\sqrt mB=\frac{nm}{B})=O(nm^{0.75})\),然而找块内找后继这一步可以用bitset,复杂度就是 \(\mathcal O(nm^{0.75}/\sqrt w)\),可以过。
- 用值域分块平衡莫队的log
- 用bitset找后继。凡是01序列都可以用bitset
分块做法(更强的火箭毛毛虫)
分块,对块内元素排序。
预处理预处理出\(f[i][j]\)表示一个数在第\(j\)块到\(i\)所在块的上一个块这部分,另一个数在\(i\)所在块的以\(i\)结尾的这部分前缀,他们之间能产生的最小答案。\(g[i][j]\)表示一个数在\(i\)所在块的下一个块到第\(j\)块这部分,另一个数在\(i\)所在块的以\(i\)结尾的这部分后缀,能产生的最小答案。令\(s[i][j]\)表示第\(i\)块的开头到第\(j\)块的末尾的答案。
询问还是分成 4 大类讨论:整 \(\to\) 整:差s数组。散 \(\to\) 整,整 $\to $ 散:查 \(f,g\)。散 $\to $散:直接归并,单次 \(\mathcal O(\sqrt n)\)
求 \(f,g\) 需要求,每个数对每个块的贡献,由于块内排序,我们可以对一个块内的所有元素到其他块的答案一起处理。每次双指针做到 \(\mathcal O(n\sqrt n)\)。
\(s\) 则又根据 \(f,g\) 递推得到。复杂度 \(\mathcal O(n)\)。
最后就是 \(\mathcal O((n+m)\sqrt n)\)。
- 分块,块内排序
- 处理散整数组,即一段散块对其后面连续的整块的贡献。
Submission #336614286 - Codeforces
2025.9.3
P9331 [JOIST 2023] 护照 / Passport - 洛谷
考基本的最短路知识。
- 到达多个点的最短路,一定是前面走了一段相同的,然后逐渐分离走向各自的终点,形如一棵树,这里到达两个点,只需要从这两个点开始建反图跑最短路即可。
- 求多点(多次询问单点)到多点的最短路就是多源最短路。
P11392 [JOI Open 2019] 三级跳 / Triple Jump - 洛谷
11:50开始,11:21吃饭,14:10到,14:35AC
自己做出
成功独立使用了”考虑两个同时存在的可行方案“与”分析目标状态性质“这两个角度分析。
后面知道这个就叫做”支配点对“,就靠调整法证明。
14:41开始17:09AC
自己做出
太搞了,\(u\) 可能大于 \(v\),在转化题意时需要注意输入限制,比如不保证 \(l\le r\)。
17:25开始,18:00走,18:40回来。第二天AC
最后没有想到[NOI2019] 弹跳技巧——Dij的本质与数据结构维护剩余集。
2025.9.4
两个角度都对了,但是没有转化成功
01序列
一个01序列形如 \(11...1100...00\) 的充要条件是有且仅有一个 ”\(10\)” 子串存在。
下降集合
这个做法我导出了 2\(\log\) 的线段树套可持久化平衡树做法。
需要发现一个观察:假设题目给出排列,那么设 \(b_i\) 为 \(i\) 的前缀最小值,那么答案就是 \(b_i=(n-i)\) 的个数。这时可以维护 \((\min_{1\le j\le i}a_j)-(n-i)\) 的最大值及最大值个数,后者为答案。
🚨 waiting to solve 🚨
Submission #336836506 - Codefrces
- 常数umap>vector>array
- "好的暴力是重要的,简洁的暴力容易优化"
- “根据题目的特殊点找思路,比如本题 \(k\) 很小,于是想与 \(k\) 有关的性质与思路”。
Submission #336851092 - Codeforces
考察了Hall定理,以及一个分析性质。
- 两个修改操作同时执行,单独看每个都很难处理,但是放一起看就有了性质。
2025.9.5
模拟赛总结:
分数220(90+30+100+0),排名18,期望得分 300(100+100+100+0)
第一题没有算空间MLE了,用容斥可以减少记录
第二题数组开小了,但开大后也只有 \(60\),复杂度为 \(nm(n+m)\log nm\) 应该是多了个 \(\log\) 导致TLE。大样例跑 \(5.5s\),时限 \(3s\)。这还不如之前想的暴力。
考试时间分配:30'T1+30'T2+130'T3+80'T2,NOIP的比赛时间还是太紧了。
Island Hopping - CodeChef ISLNDHOP - Virtual Judge
这是一个网格图,贡献是 \(|x-X|+|y-Y|\),可以直接拆绝对值+DP而不是用BFS。
- 性质:若 \(y>x\),则 \(y+x>2x\)。利用这个性质,每次值域翻倍。
18:12开始,22:11没写出来走了
现在老是想线段树,线段树维护不了就觉得做不了,都没想过分块,想分块一下子就简单了。
调试问题:仅能保证a升序,无法保证b,但后来以为也是按照b升序的。
调试心得:将每一步进行时,前面已经满足的前提以注释写出来。
Submission #337929659 - Codeforces

2025.9.11
一条路径->欧拉路径->处理度数
2025.9.12
17:25-21:35
自己做出,思路见注释,运用”从特殊情况想起“可以解决。
2025.11.19
分析性质不能泛泛而谈,最好确确实实找出几个真实的例子玩一下(画得具象一点):
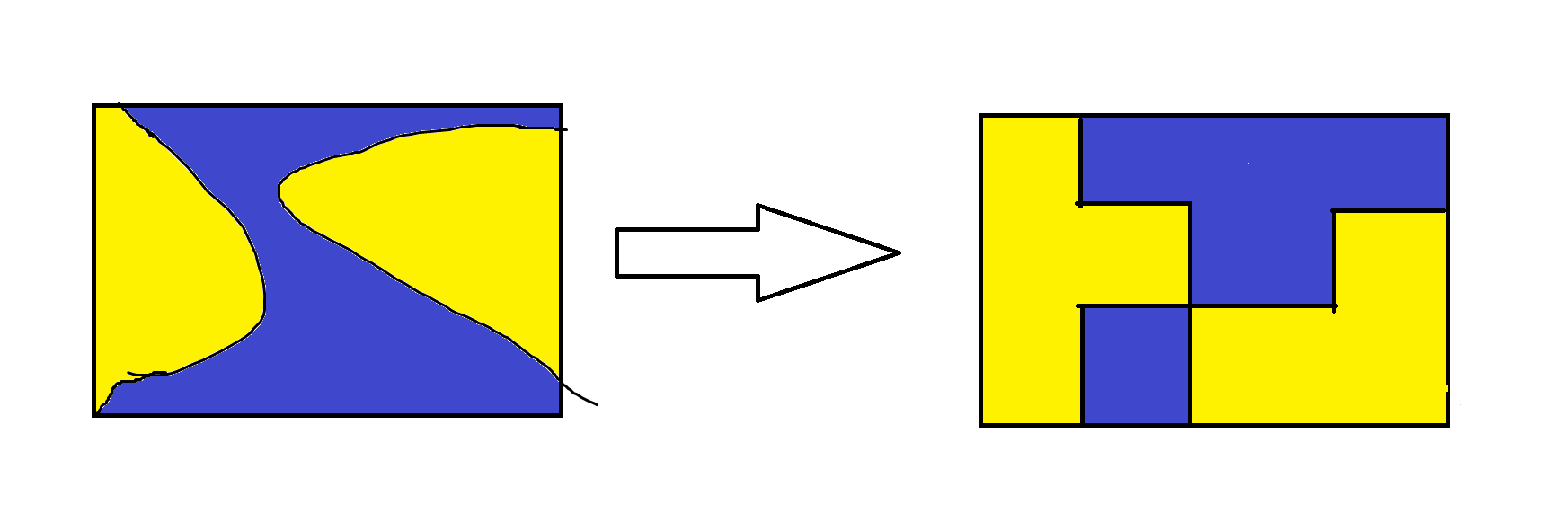
2025.11.21
构造题简直就是规律总结。除了最基本的规约、增量、调整。其他基本上就是不断总结规律。感觉没有什么套路。
考虑要让 \(|d^+(u)-d^-(u)|=1\),首先不难发现边为 \(1\) 的个数必须是奇数。然后发现,当所有边权都等于 \(1\) 时,如果每个点都向一个超级点连边,那么这个图是欧拉图,而一个合法的欧拉回路就是构造方案。
当有边权不为 \(1\) 时,我们希望 \(2\) 的边可以自己作为进出边相互抵消,然后 \(1\) 的边也是自己抵消,当 \(2\) 的边有偶数条,最后就剩下 \(1\),这是可行的,当 \(2\) 的边有奇数条,最后就剩下 \(1\),\(2\) 各一条,让这两条边方向相反,也就可以了。
具体操作是:在构造欧拉回路时,从什么边权进,就尽量从什么边权出,可以发现这样是可行的。
然后就做完了。
P6898 [ICPC 2014 WF] Metal Processing Plant - 洛谷
首先枚举 \(D(A),D(B)\),变成判断性问题,可以用2sat解决,枚举一个二分另一个可以做到 \(\mathcal O(n^4\log n)\),因为他们都单调,双指针可以做到 \(\mathcal O(n^4)\)。考虑整个限制是怎样的,设 \(D(A)<D(B)\) :
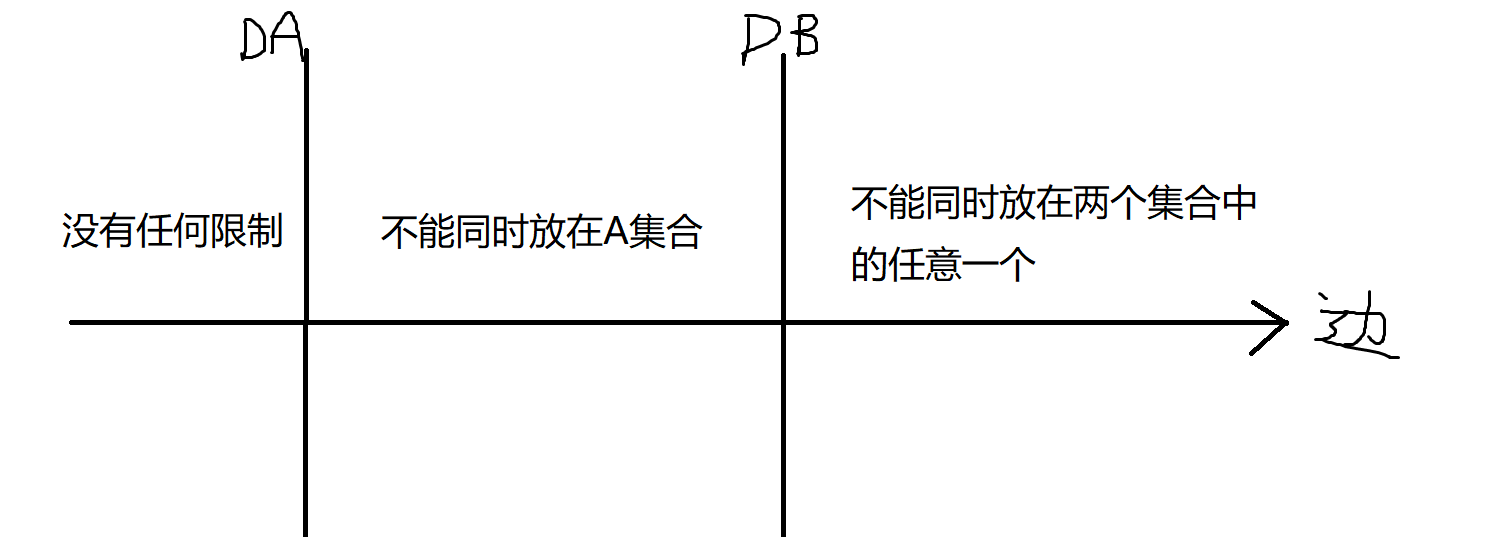
我们知道无向的 2-sat 就是并查集,对于大于 \(D(B)\) 的边的限制,就是无向的。可以先处理出那些 \(D(B)\) 的位置是会影响第三部分限制的,若一旦出现奇环则更小的 \(D(B)\) 就不可能合法,否则产生限制的是最大生成树上的边。所以枚举 \(D(B)\),二分 \(D(A)\),做到 \(\mathcal O(n^3\log n)\)。
把 Tarjan 换成 Kosaraju 可以用 bitset 优化,做到 \(\mathcal O(n^3+\frac{n^3\log n}w)\)。
考虑一个优化,在枚举 \(D(B)\) 时,\(D(A)\) 可能更新答案的上界为 \(\min(D(B),ans-D(B))\),我们一开始先 Check 这个这个上界是否可行,不可行直接跳过,可以才继续二分 \(D(A)\)。当数据随机时,每个位置的答案可以看作随机序列,而随机序列的前缀最小值个数为 \(\mathcal O(\sum_{i=1}^n\frac 1i)=\mathcal O(\log n)\),所以 2-sat 的次数就是 \(\mathcal O(n+\log^2 n)\)。一开始对点 shuffle 一下就可以对所有数据做到复杂度 \(\mathcal O(n^3)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号