APIO2025构造题讲课补题
APIO2025构造题讲课补题
第一类调整法
先给出一个“比较正确”的解法,再调整它。
[IOI 2020] 网络站点
先考虑用入栈序标号,发现不能确定 \(s\) 最后一个子树和 \(s\) 子树外的情况。可以发现这时 \(s\) 点本身的编号没有使用,可以想到用 \(s\) 本身的编号区别上述情况,这时只要把 \(s\) 的标号改为出栈序即可。
为了实现这个目的,可以考虑每层入栈、出栈序交替编号。所以还要考虑反过来,\(s\) 是入栈序,其他节点是出栈序的情况,发现这是可以的。
感觉这个技巧可以放进传统题中。
由于点权是排列,路径上点的 \(\text{mex}\) 等于路径外的点的 \(\min\)。
同样考虑一个序列是入栈序,设 \(x,y\) 的 \(lca\) 为 \(z\) \(z\to y\) 路径上 \(z\) 的儿子为 \(s_y\),发现我们不能覆盖所有入栈时间在 \([in[z],in[x]]\) 之间,和入栈时间在 \([in[s_y],in[y]]\) 之间的非链上的节点,但是这些节点的出栈序一定在 \((1,out[x])\) 和 \((out[s_x],out[y])\) 上,且不包含链上的节点,于是就做完了。
这个5个区间覆盖排除链的技巧完全可以用在传统题上。以避免数链剖分,少一个\(\log\)。
第二类调整法
题目限制“恰好为 k”,那么可以先不管这个条件给出“最大的构造方法”和“最小的构造方法”,证明之间的数都可以取到,然后逐步调整为 \(k\)。
更抽象地说,这种思路实际上是估计“最好情况”和“最坏情况”,依此来推出所有“中间情况”。所以“恰好为k”这样的条件并不是必要的。
CF1311E. Construct the Binary Tree
-
点到根距离和最小:完全二叉树
-
点到根距离和最大:链
-
逐个将链尾移动到父亲,可以逐步将答案减一,最终达到最小值。
调整即可。
-
白色点最多:铺满
-
白色点最少:
先给出答案(可以考虑一个构造,也可以直接分析),再考虑能否取到。
不妨设 \(n\le m\)
-
\(n=1\) 时 \(\min(y,m-y+1)\),因为要连通
-
\(n=2\) 时 \(m-2+[y=1\lor y=m]\)
-
\(n\ge 3\) 时,考虑下图:
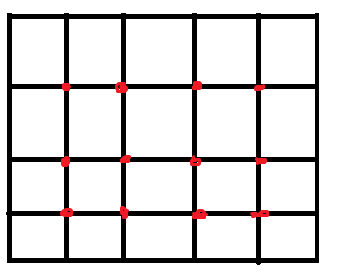
考虑条件3可以转化为每个红点旁边的4个格子中必须有白色格子。一个大小为 \(k\) 的连通块最多覆盖 \(2k+2\) 个红点,所以要求:\(2k+2\ge (n-1)(m-1)\)。
-
当 \(n,m\) 都是偶数,\(k\ge\frac{(n-1)(m-1)+1}{2}-1\)
-
否则 \(k\ge \frac{(n-1)(m-1)}2-1\)
发现当 \(x,y\) 不在边上的时候一定可以取等,在边上时答案 \(+1\),在角落答案 \(+2\)。
-
-
-
通过不断将黑点变为白点,可以取到上下界中所有情况。
然而作为构造题还要知道如何构造,先构造最小值,然后BFS扩展到 \(z\):
-
\(\min(n,m)\le 2\):特判构造,简单
-
\(n\)偶:选择第 \(\max(2,\min(n-1,x))\) 行,再正常选择其他列,如果 \(m\) 是偶数特殊处理最后一列。
-
\(n\)奇:选择第 \(\max(2,\min(m-1,y))\) 列,再正常选择其他行
CF1770H.Koxia Mahiru and Winter Festival
难以构造的方案
增量法
假设已经有了一个构造方法,将它扩展到更大的情况。
求竞赛图一条哈密顿路径
考虑增量,假设现在对于 \(1\sim n-1\) 的点有了构造方案,考虑加入点 \(n\)。
假设这条路径的点是 \(p_1\sim p_{n-1}\),分类讨论:
-
有 \(n\to p_1\) 或 \(p_{n-1}\to n\) 的边,可以直接加在链头/尾
-
否则一定有边 \(p_1\to n\to p_{n-1}\),此时一定存在一个 \(i\) 使得存在边 \(p_{i}\to n\to p_{i+1}\),将 \(n\) 放入即可。
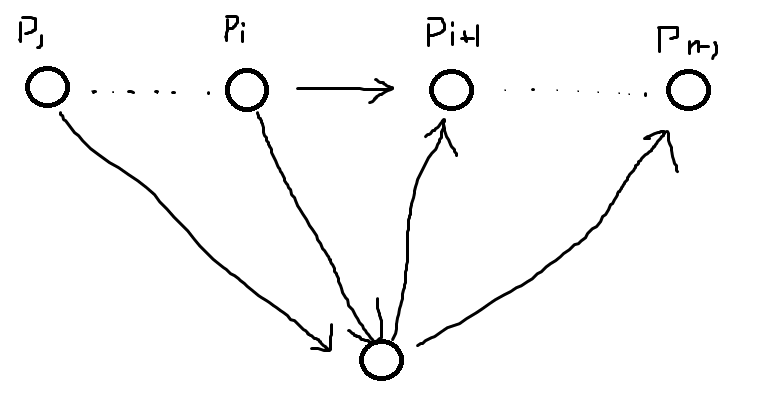
P6644 [CCO 2020] Travelling Salesperson
这道题思路与上一道题一样,假设现在有了一个前 \(n-1\) 个点的 \(p_1\to p_{n-1}\) 的路径,设其先红后蓝,且在 \(p_i\) 切换颜色。
-
如果 \((p_i,n)\) 是蓝边,则插入路径 \(p_{i-1}\to n\to p_i\) 不论 \((p_{i-1},n)\) 的颜色都是正确的。
-
否则插入路径 \(p_i\to n\to p_{i+1}\) 同理一定是正确的。
“从每个点出发"就求 \(n\) 遍,复杂度 \(\mathcal O(n^2)\)。需要注意一点细节,比如颜色全部一样时,为了不改变起点,应该将加入的放到末尾。
规约法
找到构造目标的某个部分,将它先构造掉,然后就只需考虑删掉它之后的情况。
增量规约综合。
证明存在性:发现题目没有让我们输出无解所以得证。考虑如果存在一个非关键点 \(y\) 使得距离其最近的关键点 \(x\) 到 \(y\) 的距离 \(\ge 3\),则在距离 \(y\) 为 \(1\) 的位置放置一个关键点一定不会使得两个关键点相邻。所以存在。
考虑增量法,每次加入一个点 \(x\),分类讨论:
-
如果这个点有入点被选择,那么不选 \(x\)。
-
否则如果这个点有没出点被选择,选择 \(x\)。
-
否则如果这个点有出点被选择,理应不选,但又没法保证自己被 \(2\) 步到达,难以处理。
为了避免这种情况,我们不去增量而是规约。
每次考虑一个节点 \(x\),如果已经被删除则不考虑,否则将 \(x\) 和 \(x\) 所有出点一起删除,接着计算子问题。当得到子问题的一个解时,分类讨论:
-
如果有入点被选,则不选 \(x\),这个入点已经可以2步到达 \(x\) 及 \(x\) 出点。
-
否则,选择 \(x\) ,由于其出点全部被删除,不会有上述第 \(3\) 种情况。
做完了,复杂度 \(\mathcal O(n)\)。
这道题的传统规约法不同,不一定需要”将它先构造掉“,而是先删除部分,根据子问题的解法“增量”。这种规约本质是一种增量。
#include<bits/stdc++.h>
#define int long long
#define loop(i,a,b) for(int i=a;i<=b;i++)
#define pool(i,a,b) for(int i=a;i>=b;i--)
#define pb push_back
const int NN=1e6+5;
using namespace std;
int n,m,cnt;
vector<int> ed[NN];
bool del[NN],chos[NN];
signed main(){
cin>>n>>m;
loop(i,1,m){
int a,b;cin>>a>>b;
ed[a].pb(b);
}
loop(x,1,n){
if(del[x])continue;
chos[x]=1;
for(int y:ed[x])del[y]=1;//先删除
}
pool(x,n,1){//回溯
if(!chos[x])continue;
cnt++;
for(int y:ed[x])chos[y]=0;
}
cout<<cnt<<"\n";
loop(i,1,n)if(chos[i])cout<<i<<" ";
return 0;
}
P10871 [COTS 2022] 皇后 Kraljice - 洛谷
什么神器COTS2022Day1,全是构造题。
纯手玩,各种构造方法纯手玩。
矩阵可以考虑从外向内递归 \(n\to n-2\) 然后手玩出构造方法。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号