神奇网络流真是神奇到家了

神奇网络流真是神奇到家了

U474832 语文作业

算法一

将至少选择 \(k\) 页变为至多有 \(m-k\) 页不选

将一页“选”或“不选”在图上体现出来。对于第 \(i\) 页：

• 如果选的话，会贡献 \(a_i\) 的权值，用容量为 \(1\)，费用为 \(a_i\) 的边表示。

• 如果不选，则会消耗所有包含它的区间的“不选”的次数

  将所有 \(n-m+1\) 个区间编号，建成一条链，每个区间用容量为 \(m-k\)，费用为 \(0\) 的边表示，设包含 \(i\) 的区间编号为 \([l,r]\)，那么向这条链的对应位置连接出链的边如入链的边，即可表示。

总体如下图：

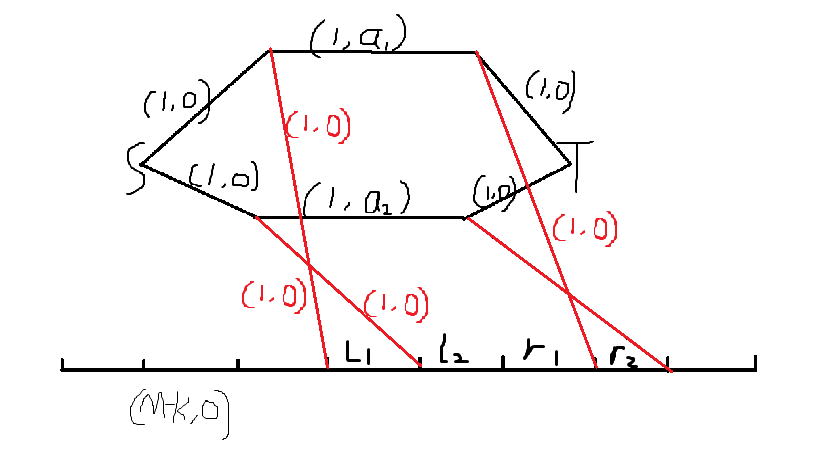
点数，边数，流量都是 \(\mathcal O(n)\)，复杂度 \(\mathcal O(n^3)\)。

算法二

将至少选择 \(k\) 页变为至多有 \(m-k\) 页不选，并且一开始选择所有的，考虑减去那些。

将所有页串成一条链，一页被减去意味着在接下来的 \(m\) 页中都要消耗一的删减次数，那么我们用如下建图方式：

• 将每个点 \(i\) 向 \(i+1\) 连一条容量为 \(\infin\)，费用为 \(0\) 的边。

• 将每个点 \(i\) 向 \(i+m\) 连一条容量为 \(1\)，费用为 \(a_i\) 的边。

• \(s\to 1\) 连一条容量为 \(m-k\)，费用为 \(0\) 的边。

• \(n\to t\) 连一条容量为 \(m-k\)，费用为 \(0\) 的边。

如下图：

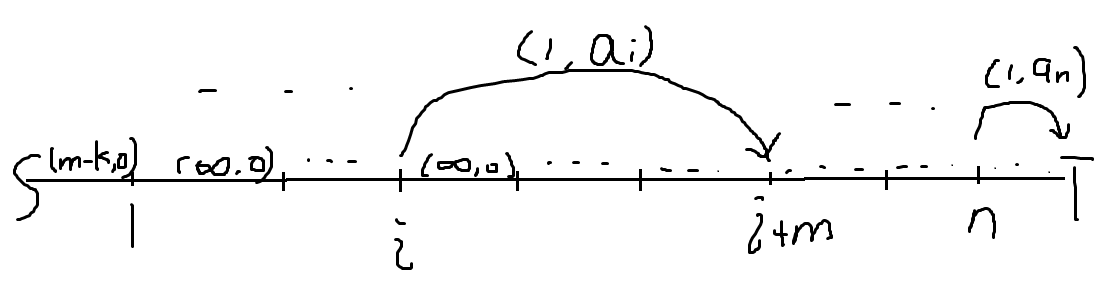
点数，边数为 \(\mathcal O(n)\)，最大流为 \(\mathcal O(m)\) 复杂度 \(\mathcal O(n^2m)\)。

P4003 无限之环

一种 网格图黑白染色 变 二分图匹配 技巧

水从一个格子流入了另一个格子，需要两个格子同时有指向对方的水管，或同时没有，这就像一个匹配。

于是可以黑白染色，变为了黑白点的匹配，最后要求完美匹配。

一个格子可以和四个不同方向的格子匹配，所以应该拆成四个点：

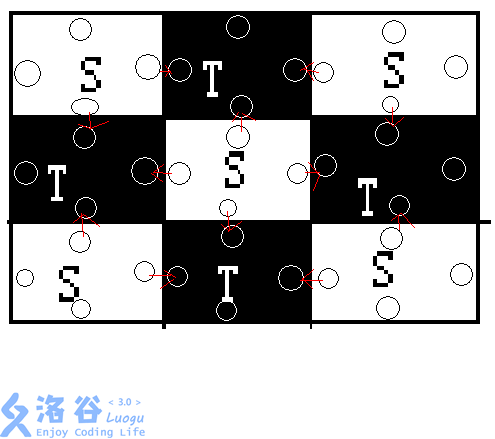
对于每个格子，一开始仅向固定方向有流，发现一次旋转其实就是改变的流的方向。

那直接通过加边可以模拟这种改变。

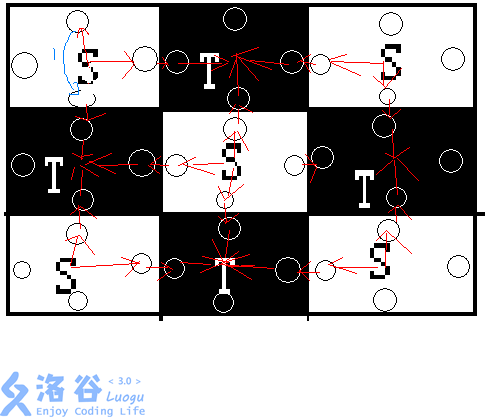
分类讨论即可。

CF1288F Red-Blue Graph

算法〇

一个naive的想法是重建一个二分图，左部表示点，右部表示边，将”\(R\) 边严格比 \(B\) 边多“转化为”\(R\) 边至少有 \(\left\lfloor\frac {deg+1}{2}\right\rfloor\) 条”对于每条边讨论，（前面表示流量，后面表示费用）如果是

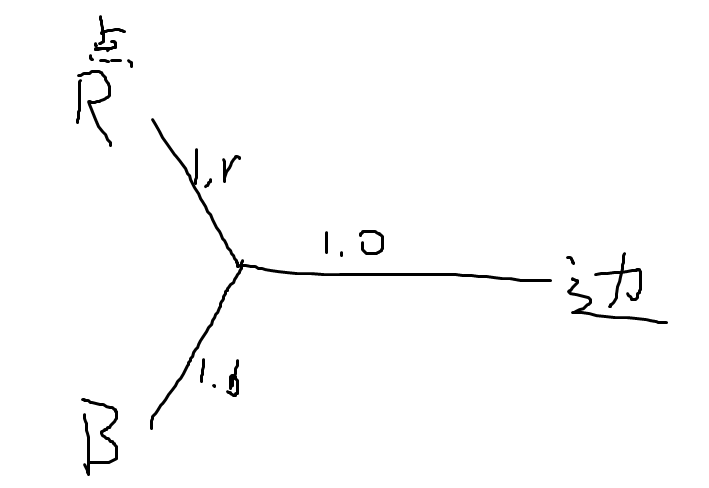
是可以解决的，但如果是

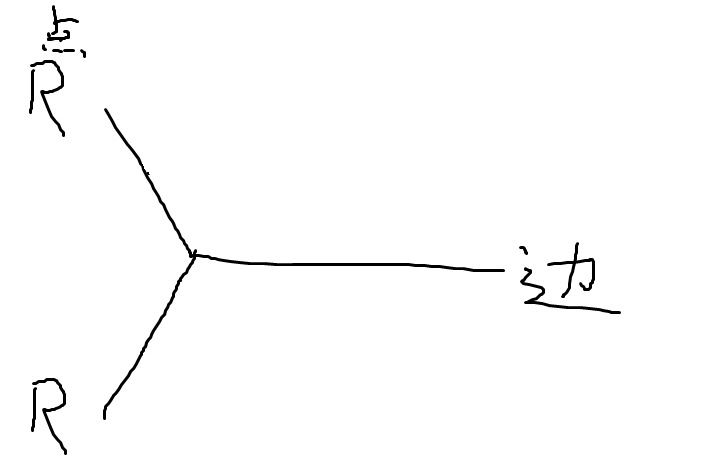
就难以解决，因为我们想要这条边要么有 \(0\) 要么有 \(2\) 的流量，这是不行的。

算法一

套路的将红色边设为 \(+1\)，蓝色边设为 \(−1\)。则问题相当于要求一些点的权值是 \(>0,<0\) 问最小费用。

我们定义一条边 \((u,v,l,r,c)\) 表示：一条从 \(u\) 到 \(v\)，下界为 \(l\)，上界为 \(r\)，费用为 \(c\) 的边。定义 \(s\) 表示源点，\(t\) 表示汇点。

具体操作是这样的：

对于原图中一条边 \((u,v)\)，我们将它拆作两条边$ (u,v,0,1,r)$ 和 \((v,u,0,1,b)\)。如果它从左往右流，则这条边是红边；如果它从右往左流，则这条边是蓝边。否则，如果它左右都不流，则这条边不染色。

我们发现，对于一条红边，左部点流出，右部点流入；对于一条蓝边，左部点流入，右部点流出。

对于左部的红点以及右部的蓝点 \(x\)，流出应该大于流入，因此连边 \((s,x,1,\infin,0)\)

对于左部的蓝点以及右部的红点 \(x\)，流入应该大于流出，因此连边 \((x,t,1,\infin,0)\)

对于一个无色点 \(x\)，因为它既可以流入，又可以流出，因此连边 \((s,x,0,\infin,0)\) 和 \((x,t,0,\infin,0)\)。

考虑一条边不会同时走来回两条边（不然不如不走），这样是正确的，然后跑最小费用可行流即可。

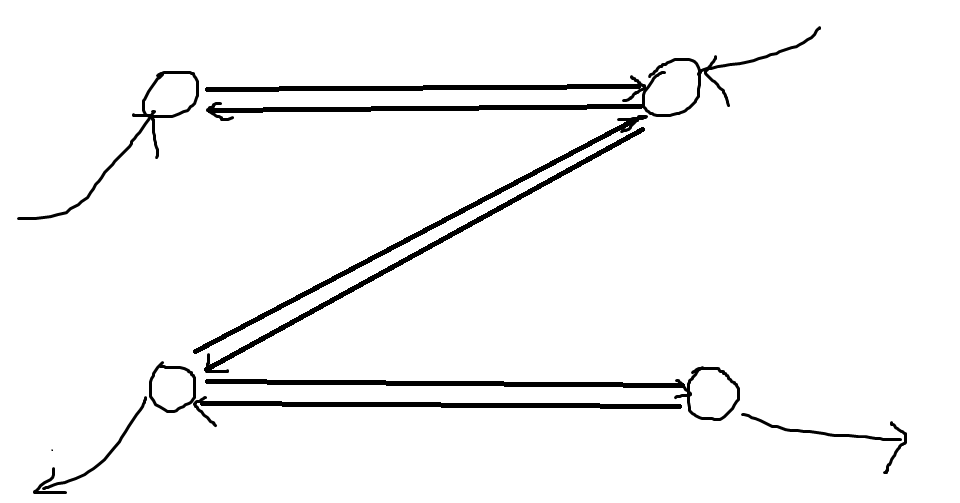
算法二：

拆边还是一样，但是最后可以不使用上下界。

对于左部的红点以及右部的蓝点，连 \((s,x,1,-\infin),(s,x,\infin,0)\)。

对于左部的蓝点以及右部的红点，连 \((u,t,1,\infin),(u,t,\infin,0)\)。

对于无色点，连 \((s,x,\infin ,0),(x,t,\infin,0)\)。

这样可以引诱网络流算法先满足严格多余的限制。

然后跑最小费用可行流。

设有色点有 \(cnt\) 个，最后 \(ans=flow+cnt\times \infin\)，如果满足了所有限制，则有 \(ans<\infin\)，否则无解。

算法三：

直接糊一手单纯形板板。每条边拆成两个变量表示是否为 R/B，满足和不大于 \(1\)。然后再对每个 R/B 点加一个限制。注意可能出现浮点数运算（加个模数就行）。

CF1307G Cow and Exercise

一个求 \(k\) 条不交路径权值和最小值的方法。

首先可以发现在最小割边上增加权值一定是更优的。

设包含这些割边的最短路径长为 \(d_1,d_2,\cdots d_m\) ，可以证明这些路径的边一定两两不交（不然交边一定成为割边）。

可以通过网络流求得这些边权，即建边 \((x,y,flow=1,cost=e(x,y))\) ，其中 \(e(x,y)\) 表示原图边权，令 \(s=1,t=n\) 跑最小费用最大流即可。

并且由于这些路径两两不交，不存在退流操作，每次的增量就是 \(d_i\)。

我们选取其中较小的 \(k\) 个 \(d_1,d_2,\cdots,d_k\) ，最后一定要使得路径变的一样长，即变为 \(q_k=\dfrac{x+\sum_{i=1}^kd_i}{k}\) ,并使得 \(\forall i\le k,d_i\le q_k,\forall i>k,d_i>q_k\)。

当 \(t\le k\) 时由于 \(d\le q_k\) 所以 \(q_t\) 不断变小 ，当 \(t> k\) 时 由于 \(d>q_k\) ，\(q_t\) 不断变大。

所以 \(q_k=\min_{i} q_i\) ！

枚举求最小值即可，复杂度 \(\mathcal O(nm^2+qm)\)。