最小割树 学习笔记

最小割树 学习笔记

正确性证明

设原图 \(G=(V,E)\)， \(\delta (W)\) 表示把点集划分为 \(W\) 与 \(V\setminus W\) 的割的费用，即 \(\delta (W)=\sum_{u\in W,v\notin W}e(u,v)\)，\(\lambda(x,y)\) 表示 \(x,y\) 之间的最小割方案中包含 \(x\) 的那个点集。\(\Lambda (x,y)\) 为 \(\lambda(x,y)\) 构成的集合。

首先明显有 \(\lambda (x,y)\cup \lambda(y,x)=V,\lambda (x,y)\cap \lambda(y,x)=\emptyset,\delta(W)=\delta(V\setminus W)\)

定理1

任取三点 \(a,b,c\)，有 \(\delta(\lambda(a,b))\ge\min(\delta(\lambda(a,c)),\delta(\lambda(c,b)))\)。

证明：

• 当 \(c\in \lambda(a,b)\)，则 \(\lambda(a,b)\) 也是 \(c,b\) 的一个割，所以 \(\delta(\lambda (a,b))\ge \delta (\lambda(c,b))\)。

• 当 \(c\in \lambda (b,a)\) 时，同理有 \(\delta(\lambda(a,b))\ge \delta(\lambda(a,c))\)

得证。

并且进一步推出对于任意 \(k\) 个不同的点 \(s_1\sim s_k\)，有 \(\delta\lambda(s\_1,s\_k)\ge\min(\delta\lambda(s\_1,s\_2),\delta\lambda(s\_2,s\_3),\cdots,\delta\lambda(s\_{k-1},s\_k))\)

定理2

\(\delta(A)+\delta(B)\ge \delta (A\cap B)+\delta (A\cup B)\)

证明：

画Venn图。

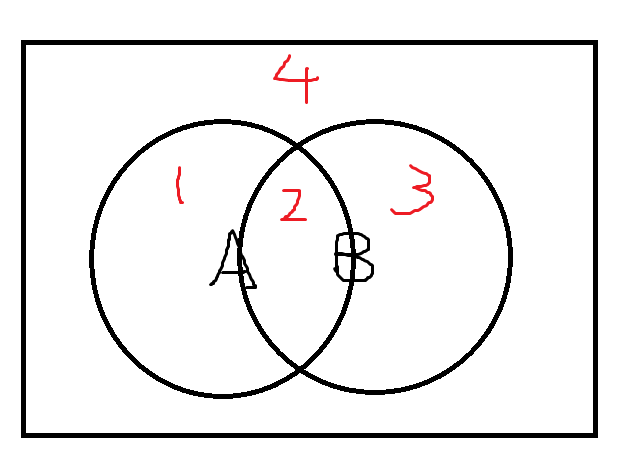
左式包含 \((1,4),(1,3),(2,4),(2,3),(1,2),(4,2),(1,3),(4,3)\)。

右式包含 \((1,4),(2,4),(3,4),(1,2),(2,4),(4,3)\)。

可以发现上面列举的严格比下面多了两个 \((1,3)\)。

得证。

定理3

\(\delta(A)+\delta(B)\ge \delta (A\setminus B)+\delta (B\setminus A)\)

证明：

同样是画Venn图。

左式包含 \((1,4),(1,3),(2,4),(2,3),(1,2),(4,2),(1,3),(4,3)\)。

右式包含 \((1,4),(1,3),(1,2),(1,3),(2,3),(4,3)\)。

可以发现上面列举的严格比下面多了两个 \((2,4)\)。

得证。

定理4

令 \(W\in \Lambda(s,t)\)，则 \(\forall u,v\in W,u\ne v,\exists X\in\Lambda (u,v),X\subseteq W\) 。

证明：

设 \(X\in \Lambda (u,v),s\in X,u\in X\)

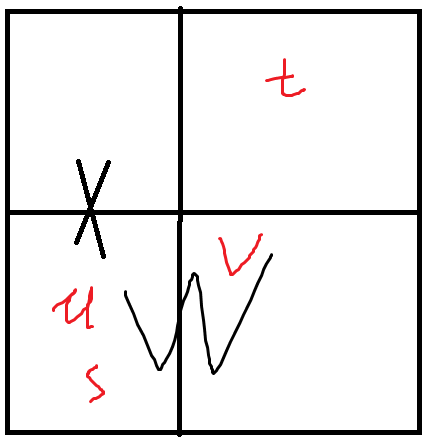
• 当 \(t\notin X\)，根据定理2，\(\delta(X)+\delta(W)\ge\delta(X\cap W)+\delta(X\cup W)\)。

  又因为 \(X\cap W\) 是 \(u,v\) 的一个割，所以 \(\delta (X\cap W)\ge \delta(X)\)

  又因为 \(X\cup W\) 是 \(s,t\) 的一个割，所以 \(\delta (X\cup W)\ge \delta(W)\)。

  所以等号成立， \(X\cap W\in\Lambda (u,v)\)。

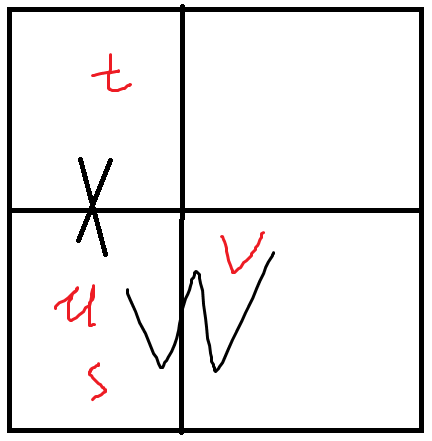
• 当 \(t\in X\)，根据定理3，\(\delta(X)+\delta(W)\ge\delta(X\setminus W)+\delta(W\setminus X)\)。

  又因为 \(W\setminus X\) 是 \(u,v\) 的一个割，所以 \(\delta (X\cap W)\ge \delta(X)\)

  又因为 \(X\setminus W\) 是 \(s,t\) 的一个割，所以 \(\delta (X\setminus W)\ge \delta(W)\)。
  所以等号成立， \(W\setminus X\in\Lambda (u,v)\)。

得证。

定理5

最小割树上两点间的边权最小值，就是两点在原图上的最小割。

证明：

设两点为 \(x,y\)，路径上的点为 \(a_1\sim a_k\)。

根据定理4并考虑构造过程可得：\(\forall i\in [1,k-1],\exists X\in \Lambda(a_i,a_{i+1})\) 使得 \(X\) 是 \(x,y\) 的割。

所以 \(\delta (\lambda(x,y))\le \min_{1\le i<k}\{\delta(\lambda(a_i,a_{i+1})\}\)

结合定理2可得： \(\delta (\lambda(x,y))= \min_{1\le i<k}{\delta(\lambda(a_i,a_{i+1})}\)

得证。