留空DP——[NOI2023] 桂花树 题解

留空DP——[NOI2023] 桂花树 题解

快进：

1. 题目等价于是把 \(m\) 个有标号点插入进 \(n\) 个节点的树上。

   一个 \(n\) 个节点的树：
   

2. 考虑 \(m=1\) 的过程，发现是把一个点插在边上，或挂在点下，那么 \(ans=2n-1\)

   挂在点下：
   

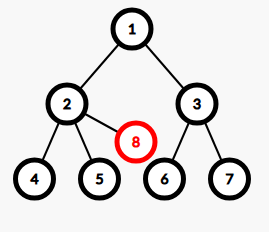
   插在边上：

   

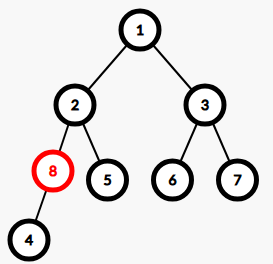
3. 然后发现从小到大用上述过程插入 \(m\) 个点，可以构造出 \(k=0\) 的所有情况。所以得到 \(k=0\) 的答案 \(ans=(2n-1)(2n+1)\cdots (2n+2m-3)\)。

4. 然后发现 \(k>0\) 的时候其实相当于多了如下方案：在一条边上插入了一条边（第2步是在一条边上插入一个点），设浅的编号为 \(x\) ，深的编号为 \(y\)，满足 \(0<x-y\le k\)。

   

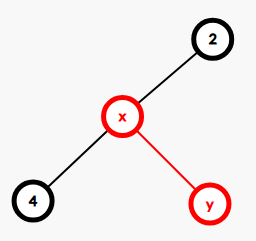
5. 因为 \(k\) 很小，所以可能状压，但边的情况太多了，直接枚举边插入容易算重（比如先插入边 \(x\to z\) 再在中间插入 \(y\)，与先插入边 \(x\to y\) 再插入 \(z\) 作为 \(y\) 的叶子是一样的）。

快进结束。

为了结合第2步的插入过程，我们还是从小到大枚举，当进行”插入一条边“操作时，仅把

深的节点 \(y\) 确定为当前节点 \(i\) 了，而把浅的节点 \(x\) 留空，成为一个待决点，待后来插入时决定。很明显 \(x\in [i+1,i+k]\)，那么只需要状压 \(k\) 个空即可。

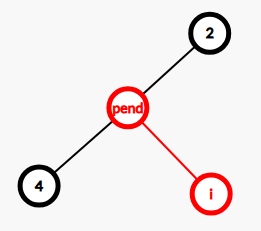
那么每个节点插入时有三种情况：设当前树上有 \(size\) 个节点

• 将 \(i+1\) 插在边上或挂在点下，系数 \(2size−1\)。

• 将 \(i+1\) 插入一条边，包含一个待决点，系数 \(size−1\)。

• 用 \(i+1\) 填上一个空白点。

转移即可，复杂度 \(\mathcal O(mk2^k)\)。