WQS 二分(与闵可夫斯基和优化dp)学习笔记
WQS 二分学习笔记(与闵可夫斯基和优化dp)
一、算法
对于函数 \(y=F(x)\) 表示选择 \(x\) 个元素的时候的权值。我们想要求 \(F(k)\) ,其中 \(k\) 是一个给定的值。
下文以 \(F(x)\) 为上凸函数为例,表示下凹函数时同理。
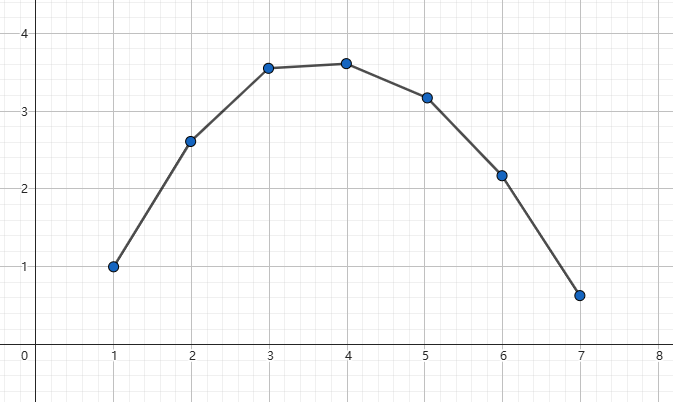
假设我们给每个元素增加一个附加限制 \(p\) ,即令 \(G(x)=F(x)+px\)。
我们发现 \(G(x)\) 就是用斜率为 \(-p\) 的直线穿过点 \((x,F(x))\) 时的截距。
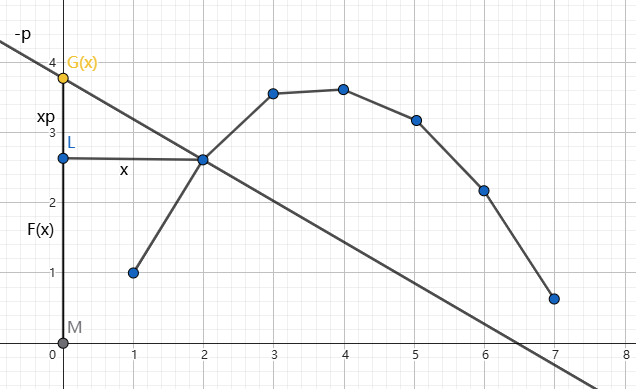
那么 \(G(x)\) 取到最大值的位置,就是斜率为 \(-p\) 的直线与函数 \(F(x)\) 的图像相切的时候。
由于 \(F(x)\) 为上凸函数的时候,其斜率单调递减。

所以你可以通过 \(G(x)\) 取到最大值的位置 \(x\) 与 \(k\) 的大小关系,来调整 \(p\) 的大小,使得其切在 \(x=k\) 的位置。
-
若 \(x>k\),则 \(p\) 太小,应该增大(即减小斜率 \(-p\))。
-
若 \(x<k\),则 \(p\) 太小,应该减小(及增大斜率 \(-p\))。
当 \(x=k\) 时,\(F(x)=G(x)-px\),于是我们就用二分+求 \(G(x)\) 最值的方式得到了 \(F(k)\) 的值。
二、凸性证明
1.根据定义证明
上凸:\(F(x)-F(x-1)\ge F(x+1)-F(x)\)。
下凸:\(F(x)-F(x-1)\le F(x+1)-F(x)\)。
意义就是每次自增自变量时产生的贡献越来越大或越来越小。
2.规约网络流
先给出网络流做法,然后WQS二分+模拟网络流。
3.四边形不等式
对于dp问题,如果 \(w(j,i)\) 有四边形不等式,那么 \(g(k):=f(n,k)\) 有凸性。
三、细节
在二分一个斜率的时候,可能切到多个点,这时这些点形成一个区间 \([L,R]\) 而当 \(k\in [L,R]\) 时,这个斜率是我们想要的,那么就应该让 check 与 二分的 if...else... 配合,其返回的切点 \(L\) 或 \(R\),使得 mid 被保留。
四、dp的输出方案
倒序处理,看dp是从哪里更新过来的。
一般dp是只需要记录 \([val,cnt]\) ,表示最值与取到最值的最小选择个数,以用于WQS二分。
若要输出方案,则要记录 \([val,l,r]\) 表示最值与去到最值的选择个数区间,可以证明一定是一个区间,然后倒序dp时使得 \(val\) 可以转移,并且 \(k\in [l,r]\) 即可。一般会列出一个不等式。
例题:20250412b木芙蓉T597081 20250412b - 洛谷。
代码:
#include<bits/stdc++.h>
#define int long long
#define loop(i,a,b) for(int i=a;i<=b;i++)
#define pool(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
const int NN=2e5+5,INF=0x3f3f3f3f3f3f3f3f;
int n,k,t,a[NN],son[NN];
struct Edge{
int u,v,w;
void read(){
cin>>u>>v>>w;
return;
}
}edge[NN];
typedef pair<int,int> pa;
vector<pa> ed[NN];
struct DPNode{
int val,l,r;//再保证val最大时,为了迎合WQS二分,还要使选的次数尽量少
DPNode operator+(DPNode b){
int _val=val+b.val;
if(_val<-INF)_val=-INF;
return {_val,l+b.l,r+b.r};
}
void operator+=(DPNode b){
*this=*this+b;
}
DPNode operator+(int x){
return {val+x,l,r};
}
DPNode operator-(int x){
return {val-x,l,r};
}
DPNode Alter(int x){
return {val,l+x,r+x};
}
bool Contain(int x){
return l<=x&&x<=r;
}
bool operator<(const DPNode&b)const{
if(val!=b.val)return val<b.val;
return l>b.l;
}
};
DPNode dp[NN][2];
int vf[NN];
int P;
DPNode max(DPNode a,DPNode b){
if(a.val<b.val)return b;
else if(a.val>b.val)return a;
return {a.val,min(a.l,b.l),max(a.r,b.r)};
}
void DP(int x,int fa){
DPNode f={0,0,0},f1={-INF,0,0},f2={-INF,0,0};//表示:没选x,选了奇数条边,选了偶数条边
son[x]=0;
for(pa eg:ed[x]){
int y=eg.first,val=eg.second;
if(y==fa)continue;
son[x]++;
vf[y]=val;//到父亲的边权
DP(y,x);
DPNode g=f,g1=f1,g2=f2;
f+=max(dp[y][0],dp[y][1]);
f1=max(g1+max(dp[y][0],dp[y][1]),dp[y][0]+max(g,g2)-val);
f2=max({g2+max(dp[y][0],dp[y][1]),(g1+dp[y][0]-val).Alter(1)+P});
}
dp[x][0]=max(f,f2+a[x]);
dp[x][1]=(f1+a[x]-vf[x]).Alter(1)+P;
return;
}
DPNode Check(int p){
for(int i=1;i<=n;i++)ed[i].clear();
for(int i=1;i<n;i++){
int u=edge[i].u,v=edge[i].v;
ed[u].push_back({v,edge[i].w});
ed[v].push_back({u,edge[i].w});
}
P=p;
DP(1,1);
return dp[1][0];
}
void Solve(int x,int fa,int c,int k){
vector<DPNode>f[3];
vector<int> chi,value;
f[0].resize(son[x]+5),f[1].resize(son[x]+5),f[2].resize(son[x]+5);
chi.resize(son[x]+5);value.resize(son[x]+5);
f[0][0]={0,0,0},f[1][0]={-INF,0,0},f[2][0]={-INF,0,0};//表示:没选x,选了奇数条边,选了偶数条边
int i=0;
for(pa eg:ed[x]){
int y=eg.first,val=eg.second;
if(y==fa)continue;
chi[++i]=y;
value[i]=val;
f[0][i]=f[0][i-1]+max(dp[y][0],dp[y][1]);
f[1][i]=max(f[1][i-1]+max(dp[y][0],dp[y][1]),dp[y][0]+max(f[0][i-1],f[2][i-1])-val);
f[2][i]=max(f[2][i-1]+max(dp[y][0],dp[y][1]),(f[1][i-1]+dp[y][0]-val).Alter(1)+P);
}
int num=-1;
auto Asif=[&](DPNode a,DPNode b){return a.val==b.val&&a.Contain(k);};//判断是否可以A\to B
auto Distr=[&](DPNode a,DPNode b){return max(b.l,k-a.r);};
auto Back=[&](DPNode a,DPNode l,DPNode r,int statu){
if(Asif(a,f[num][i])){
int consume=Distr(l,r);
Solve(chi[i],x,statu,consume);
return consume;
}
return -1ll;
};
if(c==0){
if(Asif(f[0][i],dp[x][0]))num=0;
else num=2;
}else num=1;
int lastnode=num==1?fa:-1;
k-=num==1;
assert(k>=0);
for(;i;i--){
int y=chi[i],val=value[i];
int cs=-1;
loop(lop,0,1)//先统一处理不使用的方案
if((cs=Back(f[num][i-1]+dp[y][lop],f[num][i-1],dp[y][lop],lop))>=0){
DPNode tmp=dp[y][lop];
k-=cs;
goto endpos;
}
if(num==1){
loop(lop,0,2){
if(lop==1)continue;
if((cs=Back(dp[y][0]+f[lop][i-1]-val,f[lop][i-1],dp[y][0],0))>=0){
cout<<x<<" "<<lastnode<<" "<<y<<"\n";//输出方案了
num=lop,k-=cs,lastnode=-1;
goto endpos;
}
}
}else if(num==2){
if((cs=Back((f[1][i-1]+dp[y][0]-val).Alter(1)+P,f[1][i-1].Alter(1),dp[y][0],0))>=0){
num=1,lastnode=y,k-=cs+1;//cs+1表示加上Alter(1)即本次(选择边(x,y)后完成了一次)的消耗
goto endpos;
}
}
endpos:;
}
return;
}
signed main(){
cin>>n>>k>>t;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<n;i++)edge[i].read();
int l=-1e9,r=1e9;
while(l<r){
int mid=l+r+1>>1;
DPNode res=Check(mid);
if(res.l>k)r=mid-1;
else l=mid;
}
DPNode res=Check(l);
cout<<(int)(res.val-k*l)<<"\n";//最小跨度是2有问题
if(!t)return 0;
Solve(1,0,0,k);
return 0;
}
五、闵可夫斯基和优化dp
由于同为凸包性质,可以和WQS二分共同使用。
对于 \(f_{c}=\min_{a+b=c} g_a+h_b\) 即 \((+,\min)\) 的卷积,若 \(g,h\) 有凸型,可用闵可夫斯基和计算。
即将 \(g_a\) 看作 \((a,g_a)\) 的点,\(h_b\) 看作 \((b,h_b)\) 的点。
但由于只有下凸壳:
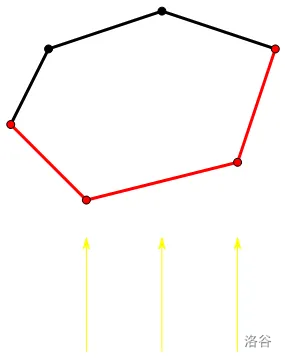
下凸壳闵可夫斯基和当然可以仿照凸包的写法。但是这里有一个更方便的写法:
考虑下凸壳的一个性质:即任意 \(x\) 坐标至多对应一个点。
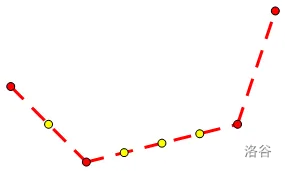
把这些点全部描述出来,我们完全可以用一个 O(值域) 的数组记录这些点值,这样就不必描述边的信息。比如上述的凸包可以用 \(\{2,1,0,\frac14,\frac12,\frac34,1,3\}\) 表示。
如果我们求出它的差分数组,由于原数组是一个凸包,所以是单调不降的。
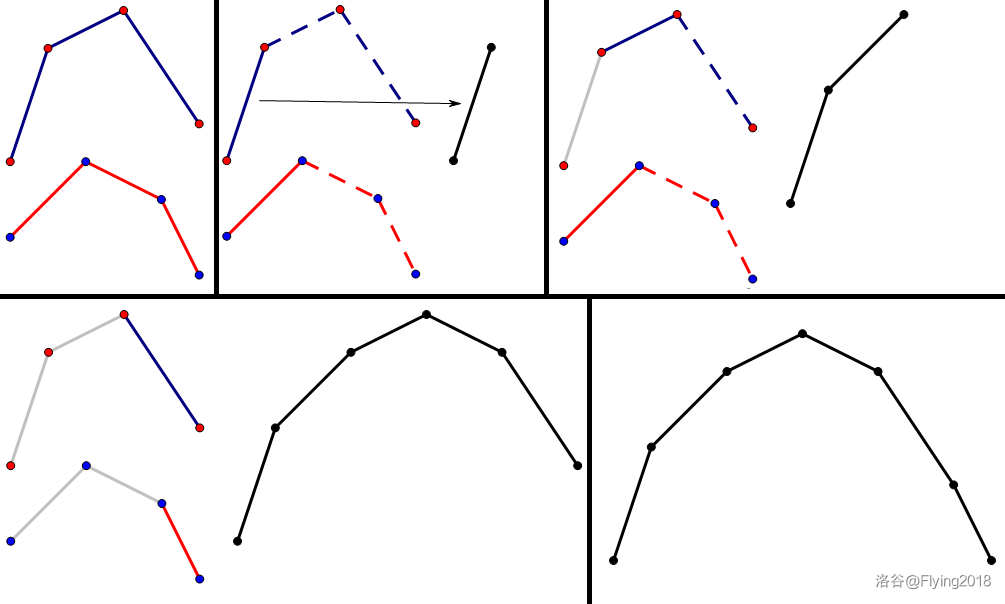
考虑求闵可夫斯基和的过程,本质上就是将两个差分数组归并排序一下。
这里用启发式合并做到 \(\mathcal O(n\log^2n)\),用可并堆做到 \(\mathcal O(n\log n)\)
演示:
例题
P5633 最小度限制生成树
首先要证明其凸性:
考虑一个无度数限制的最小生成树,其中与 \(s\) 节点连接了恰好 \(x\) 条边。
假设使 \(x\) 加1,选择一条与 \(s\) 相连的权值为 \(a\) 的边和不与 \(s\) 相连的权值为 \(b\) 的边,\(\Delta\sum w=a-b\)。根据最小权的贪心性质, \(a-b\) 一定递增。
假设使 \(x\) 减1,选择一条与 s 相连的权值为 a 的边和不与 s 相连的权值为 b 的边,\(\Delta \sum w=b-a\) 。根据最小权的贪心性质,\(b-a\) 一定向前递增,则 \(a-b\) 向后递增。
所以 \(\forall x,F(x)-F(x-1)\le F(x+1)-F(x)\) 函数下凹,可以用 WQS 二分。
这样复杂度为 \(\mathcal O(m\log m\log V)\) ,瓶颈在 Kruskal 的排序,过不了。注意到我们每次仅对一个特定的集合里的对象的权值增加,于是我们可以在开始的时候分别排序,check 时归并即可。
还要注意“细节”,详见代码。
这道题要“输出方案”。
有这样一个共线的问题。
下面把“与 \(s\) 相邻的边”称作“白边”,其他边称作“黑边”。
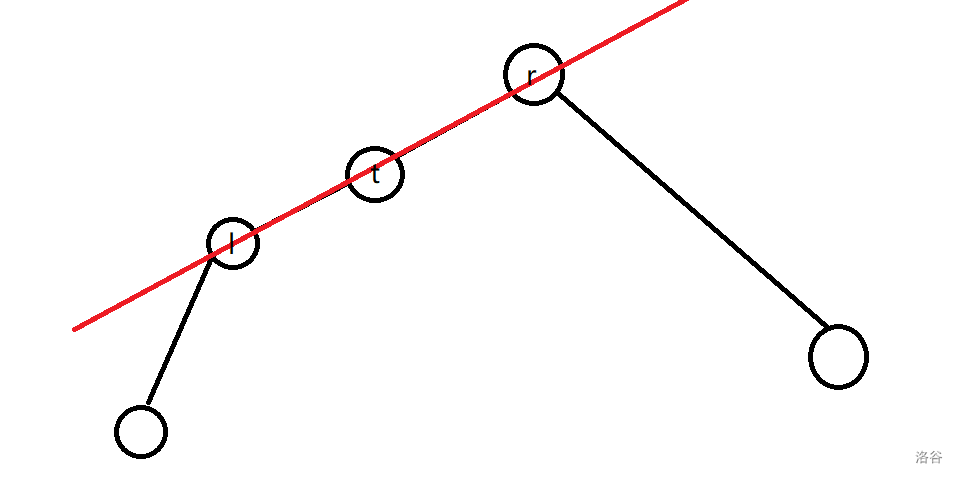
可以贴着下界(\(l\))做一次(尽量选择黑边),算出哪些白边是必要的。
然后贴着上界(\(r\))做一次(尽量选择白边),算出 \(f_i\) 表示最多有多少权值大于 \(i\) 的非必要的白边能在生成树中。
先选择所有必要的白边,然后贴着下界(\(l\))做一次,那么在构造时对于边权为 \(x\) 的非必要的白边,若 \(now+f_x<k\) 说明仅靠权值大于 \(x\) 的非必要的白边不能达到要求的 \(k\) 条边,那么加入 \(x\),这里 \(now\) 表示已经被选择的白边数。
那么构造结束后一定恰为 \(k\) 条边被选择。
Honorable Mention
题意
给定整数序列 \(\{a\}\),每次询问给出 \(l,r,k\),问在 \(a_i,i∈[l,r]\) 中选择恰好 \(k\) 个不相交(可相邻)子段的最大权值。
\(n,q\le 3.5\times 10^4,|a_i|\le 3.5\times 10^4,1\le l\le r\le n,1\le k\le r-l+1\)
做法1:每次模拟费用流
就是[这道题](Problem - 280D - Codeforces),复杂度 \(\mathcal O(qn\log n)\)。但这证明每个问题有凸性。
做法2:每次WQS二分。
那么就变成了求正数之和,复杂度 \(\mathcal O(qn\log V)\)。
做法3:一个弱化问题
考虑 \(l=1,r=n\),\(k\in [1,n]\) 这个问题。
因为答案都是凸包的形式,我们考虑凸包合并。我们尝试分治,也就是建一棵线段树,每个节点维护一个其分治区间的答案凸包 \(vec\),合并左右时,若不考虑穿过中点的子段,那 \(vec_{x,i}=\max \{vec_{ls,j}+vec _{rs,i−j}\}\),这是一个 max+ 卷积,可以闵可夫斯基和。但这样没有考虑存在一个子段穿过中点,那我们就同时维护四个凸包,\(vec_{0/1,0/1}\),意为左边第一位是否强制选择,右边第一位是否强制选择。我们用加法表示凸包合并,那么有 \(vec_{x,p,q,i}=\max\{(vec_{ls,p,0}+vec_{rs,0,q})_i,(vec_{ls,p,1}+vec_{rs,1,q})_{i+1}\}\),意为要么没有穿过中间的,要么钦定一个穿过中间的,这里 \(i+1\) 表示把两个区间合并成了一个,个数就少了一个。由于分治,复杂度是 \(O(n\log n)\) 的。
做法4:用线段树预处理
维护全局分治时的信息,就变为了一个支持动态查询的线段树。
用做法3预处理后,考虑每次询问。
发现你要对树上 \(O(\log n)\) 个区间做凸包合并,这显然是不可接受的,这时我们想起第一种做法的 wqs 二分,我们可以在最外层二分一个 \(mid\) 去掉对子段个数的限制,这样每个区间就可以只记 \(4\) 个值分别代表首、尾是否强制选时的最大子段和,而不用记四个长度为区间长度的凸包。合并的时候类似上面,但这次只用值之间相加即可,复杂度为常数级别。最后的问题是如何对于一个线段树节点对应的凸包求出在选一段加 \(mid\) 权值的情况下的最大权,这是容易的,直接在凸包上二分斜率即可。
具体做法就是,最外层二分代价 \(mid\),然后对询问区间定位到线段树上 \(O(\log n)\) 个区间对应的节点,对每个节点上的四个凸包二分求出在 \(mid\) 下的最大权和选择的段数,然后用第二种做法的合并出来,反馈给 wqs 二分看是否选够 \(k\) 个再考虑调整二分。复杂度 \(\mathcal O(n\log n+q\log^2 n\log V)\)。
做法5:整体WQS二分
整体二分如果建出结构,是一棵叶子数 O(q),深度 O(logV) 的树。一般的复杂度优化是在对于同一个树上节点下挂的询问,二分的 mid 相同,数据结构上能更优。
而这一题我们对每一层考虑。同一层节点中,总有 \(O(q)\) 个询问和查询二分出的 \(mid\),我们将 \(mid\) 从大到小排序,可以发现在内层凸包上切到的点一定单调右移。我们用一个指针维护即可。
一共 \(\log V\) 层,对于每层,每个询问的复杂度为 \(\mathcal O(q\log n)\),指针最多扫过 \(\mathcal O(n\log n)\) 个点。总复杂度 \(\mathcal O((n+q)\log n\log V)\)。
代码
#include<bits/stdc++.h>
#define int long long
#define loop(i,a,b) for(int i=a;i<=b;i++)
#define pool(i,a,b) for(int i=a;i>=b;i--)
#define vi vector<int>
#define pb push_back
using namespace std;
const int NN=35005,INF=0x3f3f3f3f3f3f3f3f;
int n,q,a[NN],iter[NN<<2][2][2];
struct SegTrNode{
vi vec[2][2];
int len;
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define vec(x) sgt[x].vec
#define len(x) sgt[x].len
}sgt[NN<<2];
bool cmp(int x,int y){
return x>y;
}
vi Convol(vi u,vi v){
vi w;
for(int i=u.size()-1;i>=1;i--)u[i]-=u[i-1];
for(int i=v.size()-1;i>=1;i--)v[i]-=v[i-1];
//归并差分
w.resize(u.size()+v.size()+10,-INF);
w[0]=u[0]+v[0];
merge(u.begin()+1,u.end(),v.begin()+1,v.end(),w.begin()+1,cmp);
for(int i=1;i<w.size();i++)w[i]+=w[i-1];
return w;
}
void Up(int p){
loop(i,0,1)loop(j,0,1){
vec(p)[i][j].resize(len(p)+10,-INF);
vi v0=Convol(vec(ls(p))[i][0],vec(rs(p))[0][j]),
v1=Convol(vec(ls(p))[i][1],vec(rs(p))[1][j]);
loop(o,0,len(p))vec(p)[i][j][o]=max(v0[o],v1[o+1]);
}
return;
}
void Build(int p=1,int L=1,int R=n){
len(p)=R-L+1;
if(L==R){
loop(i,0,1)loop(j,0,1){
if(!i&&!j)vec(p)[i][j].push_back(0);
else vec(p)[i][j].push_back(-INF);
vec(p)[i][j].push_back(a[L]);
}
return;
}
int mid=L+R>>1;
Build(ls(p),L,mid);
Build(rs(p),mid+1,R);
Up(p);
return;
}
struct Query{
int l,r,k,id,Vl,Vr;
void read(int i){
id=i;
cin>>l>>r>>k;
return;
}
bool operator<(const Query &b)const{
return Vl>b.Vl;//斜率倒序
}
}qry[NN];
struct DPNode{
int val,cnt;
DPNode(int _val=0,int _cnt=0){val=_val,cnt=_cnt;}
bool operator<(DPNode b)const{
if(val^b.val)return val<b.val;
return cnt>b.cnt;
}
DPNode operator+(DPNode b)const{
return {val+b.val,cnt+b.cnt};
}
DPNode operator-(DPNode b)const{
return {val-b.val,cnt-b.cnt};
}
};
void Reset(int p=1,int L=1,int R=n){
loop(i,0,1)loop(j,0,1)iter[p][i][j]=0;
if(L==R)return;
int mid=L+R>>1;
Reset(ls(p),L,mid);
Reset(rs(p),mid+1,R);
return;
}
struct DPOnTree{
DPNode f[2][2];
DPNode*operator[](int x){return f[x];}
};
DPOnTree Merge(DPOnTree lt,DPOnTree rt,int c){
DPOnTree res;
loop(i,0,1)loop(j,0,1){
DPNode f0=lt[i][0]+rt[0][j],
f1=lt[i][1]+rt[1][j];
res[i][j]=max(f0,f1-(DPNode){-c,1});
}
return res;
}
inline DPNode Find(vi&u,int c,int&iter,int len){//斜率为c ,vector不能拷贝,必须传引用
while(iter<len&&u[iter+1]-u[iter]>c)iter++;//u中存有0~len共len+1个点,说明第iter个点用不到,并且因为要使得cnt最小,这里不能取等
return {u[iter]-c*iter,iter};
}
DPOnTree DP(int c,int l,int r,int p=1,int L=1,int R=n){
if(l<=L&&R<=r){
DPOnTree res;
loop(i,0,1)loop(j,0,1)
res[i][j]=Find(vec(p)[i][j],c,iter[p][i][j],len(p));
return res;
}
int mid=L+R>>1;
if(r<=mid)return DP(c,l,r,ls(p),L,mid);
if(l>mid)return DP(c,l,r,rs(p),mid+1,R);
return Merge(DP(c,l,r,ls(p),L,mid),DP(c,l,r,rs(p),mid+1,R),c);
}
DPNode Get(int c,int l,int r){
return DP(c,l,r).f[0][0];
}
int ans[NN];
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++)cin>>a[i];
Build();
for(int i=1;i<=q;i++)qry[i].read(i);
for(int i=1;i<=q;i++)qry[i].Vl=-2e9,qry[i].Vr=2e9;
//k相等时,要根据二分的情况重排数列。
loop(lop,0,32){
Reset();
sort(qry+1,qry+1+q);
for(int i=1;i<=q;i++){
if(qry[i].Vl==qry[i].Vr)continue;
int mid=(qry[i].Vl+qry[i].Vr)>>1;
DPNode res=Get(mid,qry[i].l,qry[i].r);
if(res.cnt>qry[i].k)qry[i].Vl=mid+1;
else qry[i].Vr=mid;
}
}
Reset();
for(int i=1;i<=q;i++){
int k=qry[i].Vl;
DPNode res=Get(k,qry[i].l,qry[i].r);
ans[qry[i].id]=res.val+k*qry[i].k;
}
for(int i=1;i<=q;i++)cout<<ans[i]<<"\n";
return 0;
}
HT5716 生成树
题意
定义一个棵树的权值为:对于任意实数 \(\mu\),\(\sum_{i} |w_i - \mu|\) 的最小值,其中 \(\{w_i\}\) 为树上边权可重集 。
求 \(n\) 个点,\(m\) 条边的无向连通带权图最大权生成树。
\(2\le n\le 2\times10^5,1\le m\le 5\times 10^5,1\le w\le 10^9\)
解析
很容易想到 \(\mu\) 应该取集合的中位数。但是如果你考虑枚举中位数,那就亖了,因为对于所有生成树,中位数是不同且无规律的,这很难优化。
所以采用另一种思路,树的权值等于前 \(\lfloor \frac{n-1}2\rfloor\) 大的边减去前 \(\lfloor \frac{n-1}2\rfloor\) 小的边。如果 \(n\) 为奇数则中间的那个不用管。
先考虑 \(n\) 为奇数的情况。把每条边拆成正负两条边,那么问题变成了,选 \(\frac{n-1}2\) 个正边,选 \(\frac{n-1}2\) 个负边,求最大生成树,这就是一个 WQS 二分板子。
当 \(n\) 是偶数时,中间的边可以直接不求!也就是说用上述规则选取 \(n-2\) 条边即可。可以证明这样是正确的。
要说明这样是正确的,只需要说明这条边一定在剩下的没有选择的边集中,不会被误选在正负权集合中。
设这条边为 \(e\),负权边集为 \(N\),正权边集合为 \(P\)。
则在集合 \(N\cup\{e\}\) 中,\(e\) 是最小值,在集合 \(P\cup\{e\}\) 中,\(e\) 也是最小值,所以选 \(e\) 是不优的。
然后在 WQS 二分时,应该归并而非重新排序,这样减少一个 \(\log\)。
复杂度 \(\mathcal O(m\alpha(n)\log w+m\log m)\)。
标程
#include<bits/stdc++.h>
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define file(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout)
#define int long long
#define lop(i,a,b) for(int i=a;i<=b;i++)
#define pol(i,a,b) for(int i=a;i>=b;i--)
#define fi first
#define se second
#define mset(a,v) memset(a,v,sizeof a)
#define mcpy(a,b) memset(a,b,sizeof b)
#define umap unordered_map
#define pb push_back
#define pc(x) __builtin_popcountll(x)
using namespace std;
typedef pair<int,int> pa;
typedef vector<int> vi;
const int NN=2e5+5,INF=0x3f3f3f3f3f3f3f3f;
int n,m;
struct Edge{
int u,v,w;
bool operator<(const Edge&b)const{
if(w^b.w)return w>b.w;//最大生成树
}
};
vector<Edge> edge1,edge2;
int fa[NN],C;
int Find(int x){
if(x==fa[x])return x;
return fa[x]=Find(fa[x]);
}
pa Kruskal(int sl){
lop(i,1,n)fa[i]=i;
int sum=0,cnt=0,cho=0,A=0,B=0;
while(cho<C){
Edge o;int col;
if(B==m||edge1[A].w>=edge2[B].w-sl)o=edge1[A],A++,col=0;
else o=edge2[B],B++,col=1;
int u=o.u,v=o.v;
int tu=Find(u),tv=Find(v);
if(tu==tv)continue;
fa[tu]=tv;
cho++,cnt+=col,sum+=o.w-col*sl;
}
return {cnt,sum};
}
signed main(){
io;cin>>n>>m;
lop(i,1,m){
int u,v,w;cin>>u>>v>>w;
edge1.pb({u,v,w});
edge2.pb({u,v,-w});
}
sort(edge1.begin(),edge1.end());
sort(edge2.begin(),edge2.end());
int k=(n-1)/2;C=k*2;
int l=-2e9,r=2e9;
while(l<r){
int mid=l+r>>1;
pa res=Kruskal(mid);//res.fi表示负权边的最少数量
if(res.fi>k)l=mid+1;//斜率
else r=mid;
}
cout<<(Kruskal(l).se+l*k);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号