语文作业 题解

U474832 语文作业 题解

题目描述

语文老师给 hzx 与 lph 布置了语文寒假读书作业，这本书太厚了，总共有 \(n\) 页。

老师会在开学时进行检查，任意翻阅连续的 \(m\) 页，如果这 \(m\) 页里至少有 \(k\) 页进行批注，那么 hzx 与 lph 就会过关，否则就只能在地府里见着他们了。

然而，老师要求，若想在第 \(i\) 页进行批注，则需要写 \(a_i\) 个字。

lph 和 hzx 太懒了，想尽可能少写字，却又想通过检查。于是请你算一算最少需要批注几个字。

对于 \(100\%\) 的数据，\(1\leq k\leq m\leq n \leq 1000\)。

算法一：

将至少选择 \(k\) 页变为至多有 \(m-k\) 页不选

将一页“选”或“不选”在图上体现出来。对于第 \(i\) 页：

• 如果选的话，会贡献 \(a_i\) 的权值，用容量为 \(1\)，费用为 \(a_i\) 的边表示。

• 如果不选，则会消耗所有包含它的区间的“不选”的次数

  将所有 \(n-m+1\) 个区间编号，建成一条链，每个区间用容量为 \(m-k\)，费用为 \(0\) 的边表示，设包含 \(i\) 的区间编号为 \([l,r]\)，那么向这条链的对应位置连接出链的边如入链的边，即可表示。

总体如下图：

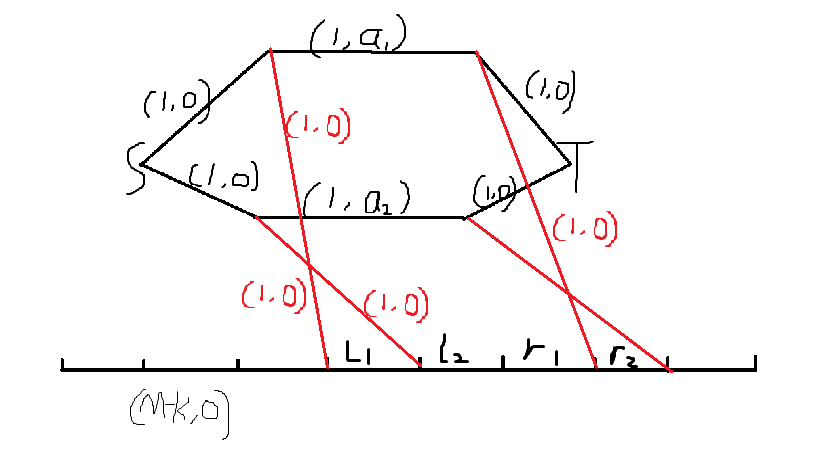
点数，边数，流量都是 \(\mathcal O(n)\)，复杂度 \(\mathcal O(n^3)\)。

算法二

将至少选择 \(k\) 页变为至多有 \(m-k\) 页不选，并且一开始选择所有的，考虑减去那些。

将所有页串成一条链，一页被减去意味着在接下来的 \(m\) 页中都要消耗一的删减次数，那么我们用如下建图方式：

• 将每个点 \(i\) 向 \(i+1\) 连一条容量为 \(\infin\)，费用为 \(0\) 的边。

• 将每个点 \(i\) 向 \(i+m\) 连一条容量为 \(1\)，费用为 \(a_i\) 的边。

• \(s\to 1\) 连一条容量为 \(m-k\)，费用为 \(0\) 的边。

• \(n\to t\) 连一条容量为 \(m-k\)，费用为 \(0\) 的边。

如下图：

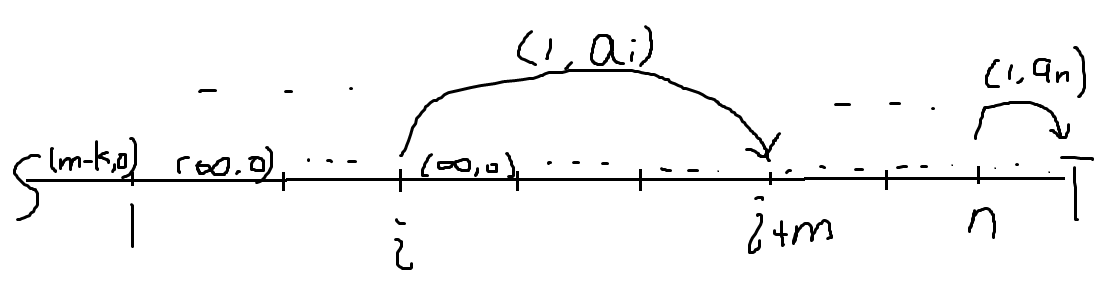
点数，边数为 \(\mathcal O(n)\)，最大流为 \(\mathcal O(m)\) 复杂度 \(\mathcal O(n^2m)\)。