做题记录（三）

做题记录

题目名称	做题时间	题目标签
Wormhole Sort S	2024.1.25
一双木棋	2024.1.25
洪水	2024.1.26	DDP
邮局	2024.1.26
Lawrence	2024.1.27
系统设计	2024.1.29	字符串Hash
最长双回文串	2024.1.30	Manacher
水管局长	2024.1.30	LCT
魔法森林	2024.1.30	LCT
背单词	2024.1.31	字典树
美味	2024.1.31	构造，主席树
战略游戏	2024.2.1	园方树
Victor and String	2024.2.1	回文树
Z 函数与manacher	2024.2.2	利用前期同等信息
KMP与回文自动机	2024.2.2	失败指针
Prefixes and Suffixes	2024.2.2
L 语言	2024.2.2
销售基因链	2024.2.3	特殊字符定位法
OKR-Periods of Words	2024.2.3
生成魔咒	2024.2.3

Wormhole Sort S

2024.1.25

题目做法

观察性质

1. 虫洞是双向的，且可以无限使用

2. 若选用了一个小的，则选用所有比它大的不会使答案更劣

3. 最终要使\(\forall i\in [1,n],i与p_i联通\)

那么双向的边联通问题，很明显可以用并查集。

关于判断最终答案，如果直接搜索，会超时

观察性质

1. 为使所有的都满足，有一个不满足就不用搜索了。
2. 随着虫洞增多，先前满足的也不用再搜索了。

于是我们可以使用一个从1到n的指针。经行判断。

代码：

sort(hole+1,hole+1+m);
int j=1;
while(j<=n&&Find(j)==Find(p[j]))j++;
if(j==n+1){
    cout<<-1;
    return 0;
}
for(int i=1;i<=m;i++){
    int a=hole[i].a,b=hole[i].b;
    if(Find(a)==Find(b))continue;
    fa[Find(a)]=Find(b);//注意：并查集一定是祖先相连 
    while(j<=n&&Find(j)==Find(p[j]))j++;
    if(j==n+1){
        cout<<hole[i].w;
        return 0;
    }
}

题目反思

• 关于分析题目：题目->数学语言/信息学语言->样例验证

• 关于优化：找到更新不变的量、不变的关系

一双木棋

2024.1.25

题目做法

观察性质，首先将每一行当作整体

1. 对于每一列来说，由于他只能从上到下依次摆放，所以记录高度就能确定一列的状态
2. 对于行之间，左一个的高度必须大于等于右一个的高度。
3. 双方的决策为min-max对抗搜索。

所以我们可以直接搜索做。

将这几行的高度hash一下状态压缩为一个long long数，结合unordered+map进行记忆化就行了

题目反思

关于二维的点问题，可以将一行或一列当作一个整体，将二维问题变为一维问题

洪水

2024.1.26

题目做法

观察性质

1. 图形是一棵树，不断修改权值

2. 目标是从子树内删除若干个点使根不与叶子联通的最小权值。

易得方程\(f_i=\min(w_i,\sum_{j\in son(x)}f_j)\)

由于在修改权值，所以这是一个DDP，按照套路:

1. 首先将树链剖分的重儿子分出来，得：\(f_i=\min(w_i,f_{hvy[i]}+g_i)\)其中\(g_i=\sum_{j\in son(x)\wedge j\neq hvy[x]}f_j\)

2. 接着统一转移方程形式,使其一块只与重儿子有关，一块只与本身有关：\(f_i=\min(0+w_i,f_{hvy[x]}+g_i)\)

3. 设计矩阵运算：\(C=A*B\iff C_{i,j}=\min\{A_{i,k}+B_{k,j}\}\)

4. 设未知转移方程：\(\begin{pmatrix}f_{hvy[i]}&0\end{pmatrix}*\begin{pmatrix}u_1&u_2\\u_3&u_4\end{pmatrix}=\begin{pmatrix}f_i&0\end{pmatrix}\)

5. 展开得：\(\left\{\begin{aligned}f_i=min(f_{son[i]}+u_1,0+u_2)\\0=min(f_{son[i]}+u_3,0+u_4)\end{aligned}\right.\)

6. 解得\(U=\begin{pmatrix}g_i&w_i\\\infin&0\end{pmatrix}\)

7. 用模板树剖+矩阵线段树维护即可

题目反思

DDP基本步骤

1. 找到原始方程

2. 分出重儿子

3. 统一方程形式

4. 设计运算

5. 设出转移矩阵，展开求解

DDP不变之处

• 矩阵线段树

DDP变化之处

1. 树剖时的初始状态更新——需要原始DP数组与转移矩阵，最终用转移矩阵代替原始DP数组

2. 每次更新时的轻边之间的转移

系统设计

2024.1.29

题目做法

观察性质：

1. a序列会改变，但树的形态不会改变

2. 给定的序列固定，其遍历的节点也随之固定

3. 最终有效的（让遍历节点更改的）序列一定是 \(l\sim r\) 的一个前缀。且最终答案的前缀序列的任意前缀一定合法，其余前缀不合法。也就是说具有单调性。

4. 从 \(x\) 出发可以看作从根节点 \(root\) 走到 \(x\) 在接着走。

于是可以预处理出树上任意遍历前缀。接着用二分 \(l\sim r\) 的前缀，并加上 \(root\sim x\) 这段路径，看是否在之前的预处理中出现过。那么这个可以用 Hash 进行快速比较。

细节：二分的左端点应为 \(l-1\)，因为它可以一步不走。

这里是用树状数组维护待修改的序列前缀Hash

题目反思

不论是树还是序列，段匹配问题可以用 Hash 解决。对于本题来说，是树上遍历顺序与序列的匹配，遍历顺序与序列都是连续的。

最长双回文串

2024.1.30

题目做法

观察性质：

1. 在manacher算法中，回文串边界一定是#

2. 两个连着的回文串左右的#一定有共用

维护最长回文半径 \(p[i]\) 的同时，再分别维护两个东西，以 \(i\) 为开头的最长回文子串的长度 \(ll[i]\)，和以 \(i\) 为结尾的最长回文子串的长度 \(rr[i]\)。

那么在更新 \(p[i]\)时，我们可以先算到最远边界，也就是：

\(ll[i-p[i]]=\max p[i],rr[i+p[i]]=\max p[i]\)

在计算完这些之后，便向更小的范围更新，也就是：

\(rr[i]=\max(rr[i],rr[i+2]-2),ll[i]=\max(ll[i],ll[i-2]-2)\)

接着枚举每个#就行了

题目反思

在manacher算法中，回文串边界一定是#。在处理时，可以从#下手

水管局长

2024.1.30

题目做法

删边->连边->最小生成树 + 连边删边->LCT,

LCT维护MST

题目反思

LCT维护边权需要化边权为点权：

link(u,v); -> link(u, id),link(v, id);

魔法森林

2024.1.30

题目做法

观察性质：

1. 与a,b两个有关，并分别去路径上的最大值。求和最小值

于是可以将边对 a 排序，接着以 b 为权值动态维护MST。固定一维信息，将a从小到大排序，则每次加入的边的a一定是当前最大的a 。接着统计出，每个 a 时的答案，取最小值。这个用LCT可以维护

题目反思

1. 开数组不取决于用多少，而取决于最大下标是多少

2. Root()函数可以代替并查集（动态并查集？）

3. 与多个元素有关时，可以通过排序，限制一维元素的取值，从而单独考虑其他维度。（CDQ?）

背单词

2024.1.31

题目做法

分析易得只有第三个有用

于是要让一个字符串的后缀先放

且其最大后缀放的时间与其本身放的时间应尽量靠近

1.建出字典树

因为是求后缀，所以可以先建出字典树

2. 重构树

跳过白点，保留红点（白点无用，可以忽略）

3.以子树大小排序

树越小，越先出来，让别的子树等的时间越少，并且不可能出来，因为子树小，那么子树的子树更小

4.遍历重构树

计算答案

void ReDFS(int x){
    int dfn=++cnt;
    for(int y:ed[x]){
        ans+=1+cnt-dfn;
        ReDFS(y);
    }
    return;
}

题目反思

重构字典树，找到结尾节点(有点像虚树)

美味

2024.1.31

题目做法

异或最大值，显然是要构造数

直接构造 \(ans=a_i+x\) 这一个整体，那么只需要看是否存在一个\(a=ans-x\)就行了，因为构造的数其实是一个半已知数，接着逐步缩小\(a\)的范围

假设从高到低处理到第 \(i\) 位(从右往左数,个位是第 \(0\) 位),设\(i+1\sim 18\)为求出的 \(a[i]\) 的答案为 \(ans\)

若第 \(b\)的第\(i\)位是 \(1\),那么我们希望它是长这样的

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b:−−−1∗∗ ∗\\ (min)a[j]+x:−−−0\ 0\ 0\ 0\\ (max)a[j]+x:−−−0\ 1\ 1\ 1\\ \]

容易求出\(a[i]∈[ans−x,ans−x+(1<<i)−1]\)

同理当 \(b\) 的第 \(i\) 位是 \(0\) 时\(a[i]∈[ans−x+(1<<i),ans−x+(1<<i+1)−1]\)

我们可以直接主席树上查询对于第\(i\)个人的\(l_i\sim r_i\)内有无\(a[i]\)满足上述条件

• 当b的第i位是1时，若有这样一个\(a[i]，ans+=0<<i，\)反之\(ans+=1<<i\)
• 当b的第i位是0时，若有这样一个\(a[i]，ans+=1<<i，\)反之\(ans+=0<<i\)

题目反思

1. 构造答案：将所有有关的值当作一个整体构造最终的答案。

2. 将区间加 \(x\) 再求 \(l\sim r\) 的数可以看作求\(l-x\sim r-x\)的数

3. 构造答案法解最大异或和，\(O(Nlog^2A)\)

战略游戏

2024.2.1

题目做法

首先使用 Tarjan 算法建出圆方树，然后答案就是 圆方树 上包含所有关键点的最少点数联通块 的圆点数量 减去 关键点的数量。

对园方树的关键点按照其dfn序进行排序，答案就是相邻两点

题目反思

dfn序性质：

1. 任意子树是连续的

2. 以 \(x\) 为根的子树就转化为了 \([dfn_x​,dfx_x​+siz_x​−1]\)。

3. 唯一确定一个节点，用于Tarjan

4. 对于树上若干关键点，将其以dfn序排序，相邻两点距离之和（包括第一与最后）为它们最小联通块的边数的两倍

Victor and String

2024.2.1

题目做法

题目反思

Z 函数

2024.2.2

题目做法

结论

对于 \(i>0，\)对任意\( 0≤l<i \)都可以递推得：

\(\forall 0≤x<\min(z(i−l),l+z(l)−i),s[(i)+(x)]=s[(0)+(x)]\)

感性理解

以上定义我们可以得到，在模式串 b 中，[0,nxt[k]−1] 和 [k,p] 两段是相等的。如下图所示，蓝方框是相等的：

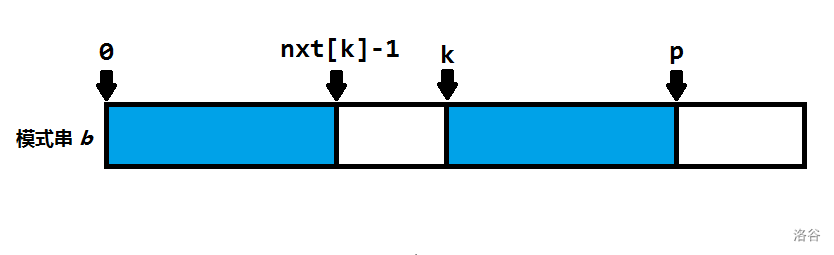
所以绿方框相等

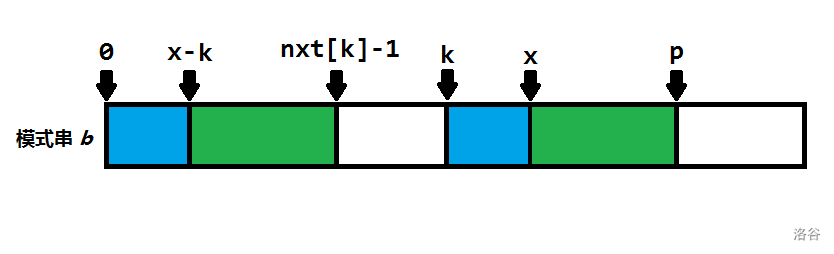
所以灰方框相等

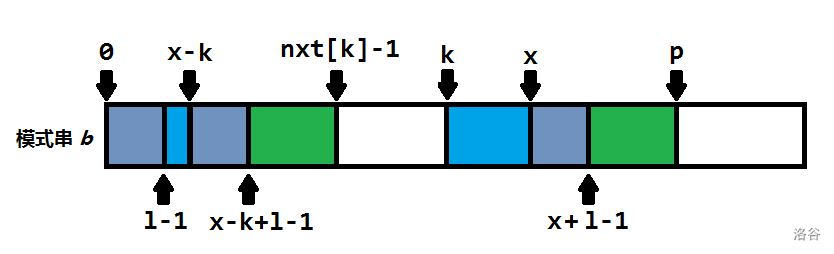
接着暴力扩展

证明

\(    \ S[(i)+x]\\=S[(l)+(i+x-l)]\\=S[(0)+(i+x-l)]\color{Red}{(x\le l+z(l)-i)}\\=\color{black}S[(i-l)+(x)]\\=S[(0)+(x)]\color{Red}(x\le z(i-l))\)

题目反思

与manacher类似，一个是对称，一个是平移，运用前面已有的内容

L 语言

2024.2.2

销售基因链

2024.2.3

生成魔咒

2024.2.3