取消等价转移——CF771E题解

取消等价转移——CF771E题解

---

很容易设出 \(dp_{i,j}\) 表示第一行选到 \(i\)，第二行选到 \(j\) 的方案数

首先考虑部分分。

\(|a_i|\le 1\)，那么产生贡献的一个矩阵不会超过 \(2\)，那么就没必要考虑 \(|i-j|\ge 4\) 的状态了。证明如下：

不妨设 \(i<j\)，那么我与其从 \(dp_{i,j}\to dp_{i,j+2}\) ，不如通过 \(dp_{i,j}\to dp_{i+2,j}\to dp_{i+2,j+2}\)，这一定是不会更劣的，因为 \(dp_{i,j+2}\to dp_{i+2,j+2}\) 不会更优。

同理另一个部分分只需要考虑 \(|i-j|<20\) 的情况即可。

顺着这个思路，我们发现其本质是，如果有对于任意状态 \(dp_{i,j}\)，如果是单独更新一行的话，我们没必要同时对一维增加两次。

于是对于所有 \(i\)，我们只需要记录状态 \(dp_{i,i}\)（以方便两行更新），以及 \(\min j_1\text{ st.}dp_{j_1,i}=dp_{i,i}+1\) 与 \(\min j_2\text{ st.}dp_{i,j_2}=dp_{i,i}+1\) 即可。

这样就只有 \(\mathcal O(n)\) 个状态。复杂度 \(\mathcal O(n)\)。

---

但是这有很多实现细节，还有另一种思路。

对于一个状态 \(dp_{i,j}\) 来说我们设 \(lstA[i]\) 表示最大的 \(k\) 使得第一行 \([k+1,i]\) 中存在一个和为 \(0\) 的矩形，\(lstB[i]\) 同理为考虑第二行的。\(lstC[i]\) 同理表示同时考虑两行的大矩形。

那么 \(dp_{i,j}=\max\{dp_{lstA[i],j},dp_{i,lstB[j]},dp_{lstC[\min\{i,j\}],lstC[\min{i,j}]}\}+1\)

将这个转移看作是从 \((n,n)\) 通过以下三种转移到达\((0,0)\) 的过程

• \((i,j)\to (lstA[i],j)\)

• \((i,j)\to (i,lstB[j])\)

• \((i,j)\to (lstC[\min(i,j)],lstC[\min(i,j)]\)

根据思路一分析的性质，当 \(lstA[i]\ne lstB[j]\) 的时候，先走第一条还是第二条转移是等价的，于是我们规定走 \(lstA[i],lstB[j]\) 更大的那一条，这一定包含原来所有的转移过程，得到正确的答案。

这样一来，先不考虑形如 \((i,i)\) 的状态，所有可以转移到的合法状态满足性质：若存在合法状态 \((i_i,j_1)\) 则一定不会存在状态 \((i_2,j_2)\) 使得 \([i_1<i_2]\oplus [j_1<j_2]=1\)。

画图理解就是

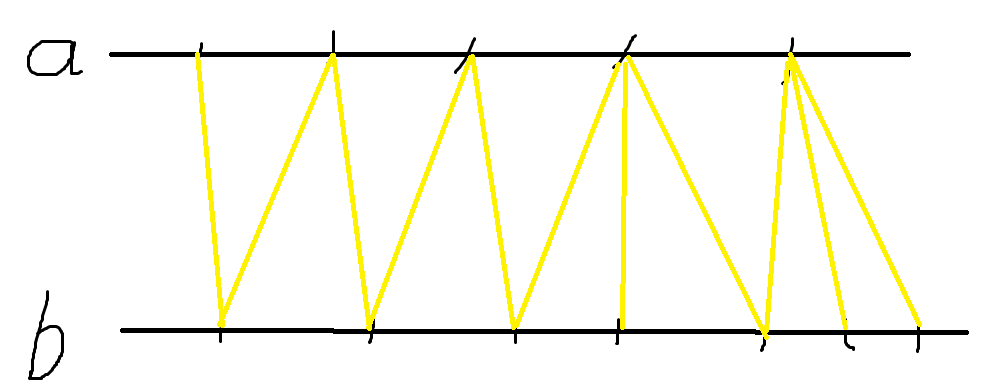
其中所有的黄线就是合法状态

简单的说就是所有合法状态偏序，由于两维的状态的范围都是 \([1,n]\)，不难分析出仅有 \(\mathcal O(n)\) 的状态合法。
加上 \((i,i)\) 的状态也只有 \(\mathcal O(n)\) 个状态合法。

于是直接记忆化搜索即可。

总结

• 通过分析转移性质从而减少状态一个 remarkable 的技巧。

• 把dp转移看作边，当两类边的行走不分先后（即先1后2与先2后1等价），应该考虑只走其中一个。

• 不要扭着看似正确的思路想，分析特殊性质是很有用的。

• 设 \(lst\) 的更新，即找最大的满足可以累加贡献或满足限制的位置。

注意

转移的时候要比较 \(lstA\) 与 \(lstB\) 而不能是 \(i,j\)，否则当一边已经无路可走即 \(lst=-1\) 的时候会错，给一个 hack：

4
9 9 9 9
1 -1 4 -4

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int NN=1e6+5,INF=0x3f3f3f3f3f3f3f3f;
int n;
int dp[NN][3],a[NN],b[NN],lstA[NN],lstB[NN],lstC[NN];
unordered_map<int,int> pos,g[NN];
int DFS(int u,int d){
    if(u<0||d<0)return -INF;
    if(!u&&!d)return 0;
    if(g[u].count(d))return g[u][d];
    int res=0;
    if(lstA[u]>lstB[d])res=max(DFS(lstA[u],d)+1,res);
    else   res=max(DFS(u,lstB[d])+1,res);
    int lst=lstC[min(u,d)];
    g[u][d]=max(res,DFS(lst,lst)+1);
    return g[u][d];
}
signed main(){
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i],a[i]+=a[i-1];
    for(int i=1;i<=n;i++)cin>>b[i],b[i]+=b[i-1];
    memset(lstA,-1,sizeof lstA);pos[0]=0;
    for(int i=1;i<=n;i++){
        if(pos.count(a[i]))lstA[i]=pos[a[i]];
        pos[a[i]]=i;
        lstA[i]=max(lstA[i],lstA[i-1]);//巧妙，这样就处理了“空格子不选的问题” 
    }
    unordered_map<int,int>().swap(pos);
    memset(lstB,-1,sizeof lstB);pos[0]=0;
    for(int i=1;i<=n;i++){
        if(pos.count(b[i]))lstB[i]=pos[b[i]];
        pos[b[i]]=i;
        lstB[i]=max(lstB[i],lstB[i-1]);
    }
    unordered_map<int,int>().swap(pos);
    memset(lstC,-1,sizeof lstC);pos[0]=0;
    for(int i=1;i<=n;i++){
        if(pos.count(a[i]+b[i]))lstC[i]=pos[a[i]+b[i]];
        pos[a[i]+b[i]]=i;
        lstC[i]=max(lstC[i-1],lstC[i]);
    }
    cout<<DFS(n,n);
    return 0;
}