pollard rho 学习笔记

pollard rho 二次学习笔记

适用问题

现在我们要实现这样一个问题：对于一个大合数 \(n(n \approx 10^{18})\)，找到其任意一个非平凡因子（就是除去 \(1\) 和 \(n\) 的因子）。

一些朴素的想法

我会暴力！因为 \(n\) 是合数，其最小非平凡因子 \(p\le \sqrt n\)，所以直接遍历是 \(\mathcal O(\sqrt n)\) 的复杂度，无法接受。

我会判断答案！我们发现，虽然找到一个因子 \(p\) 是很难的，但是给一个正整数 \(p\) 去判断其是否是 \(n\) 的因数是简单的，直接看判断 \(n\bmod p=0\)。于是可以每次随机一个数并检验，这样下一次成功的概率为 \(\frac {d(n)}{n}\) 而 \(\max_{i\le 10^{18}}d(i)\approx 10^5\)，则一次成功的概率约为 \(10^{-12}\)，这太低了。

我会 gcd！我们发现寻找两个数的 gcd 是有求解性（非判定性）的 \(\mathcal O(\log n)\) 的算法的，于是只需要每次找一个数 \(p\) 然后判断 \(\gcd(p,n)>1\) 即可，这样最坏情况下一次成功概率为 \(\frac {1}{\sqrt n}=10^{-9}\)，要大了许多，但还是不够。

“一个数的因子不可求解而两个数的gcd却可快速求解”这一性质是 pollard rho 的关键。

pollard rho的初步思想

假设 \(n\) 的一个因子为 \(p\)，那么我们随便选择若干不重复正整数 \(\{x_i\}\)，使得 \(\forall i,j,x_i\not\equiv x_j\pmod p\) 的概率为 \(\frac{p^{\underline {|\{x_i\}|}}}{p^{|{x_i}|}}\)。这是因为 \(|\Z_p|=p\)，根据生日悖论原理，我们期望取 \(\mathcal O(\sqrt p)\) 个数时满足 \(\exists i,j,x_i\equiv x_j\pmod p\)，这时 \(\gcd(|x_i-x_j|,n)\) 便是 \(n\) 的一个非平凡因子。

考虑将这样的随机过程确定下来，我们可以构造一个随机自映射 \(f:\Z_p\to \Z_p\)，即 \(f\) 映射再 \(\Z_p\) 上是确定的，即 \(\forall x\equiv y\pmod p,f(x)\equiv f(y)\pmod p\)。

这样 \(x\leftarrow f(x)\) 的过程走出了一个 \(\rho\)，成环的地方就是我们想要的。

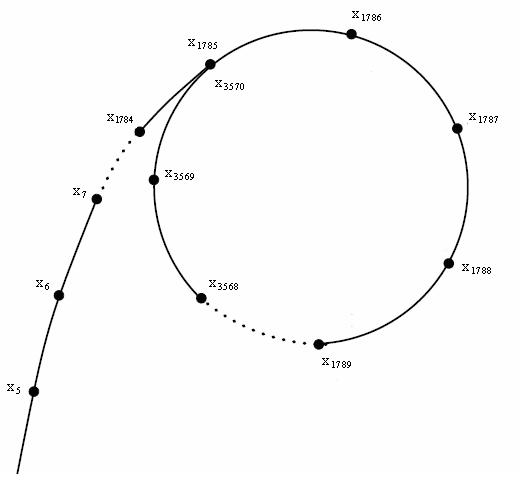
然而根据 \(p\) 去构造 \(f\) 不现实，我们可以构造 \(f(x)=(x^2+c)\bmod n\)，其中 \(c\) 是一个 \([1,n]\) 的随机数，来作为随机生成函数。而这样一个函数恰好满足需要的两个性质：

• \(\forall p|n,f\) 在 \(\Z_p\) 上随机。

• \(\forall p|n,f\) 满足自映射性质，证明显然。

现在就只需要考虑如何判断成环即可。

判环

假设两个人在赛跑，A 的速度快，B 的速度慢，经过一定时间后，A 一定会和 B 相遇，且相遇时 A 跑过的总距离减去 B 跑过的总距离一定是圈长的倍数。

一开始 \(a=b\) 每次 \(f(a)\to a,f(b)\to b\) 这样每次是需要检查 \(\gcd (|a-b|,n)>1\)，这说明在 \(\forall p|\gcd(|a-b|,n)\) 的 \(\Z_p\) 上都成环了，而 \(\gcd (|a-b|,n)\) 又正是我们想要的。

若 \(\gcd (|a-b|,n)=n\) 我们失败了，并且以后都不会成功，因为 \(\forall p|n,p\) 总是同时成环，这时就要重新随机一个 \(c\) 再次处理。设 \(p\) 为 \(n\) 的最小质因数，复杂度 \(\mathcal O(\sqrt p\log n)\)。

这种判环方法叫做 floyed 判环，需要对 \(n=4\) 的情况进行特判。

由于“倍增优化”只对brent 判环有正确性保证，这里就不介绍了。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,c;
mt19937_64 rnd(time(0));
int f(int x,int n){return ((__int128)x*x+c)%n;}
int pollard_rho(int n){
	if(n==4)return 2;//floyed判环刚好解决不了n=4的情况，这是一个巧合。 
	c=rnd()%n+1;
	int x=rnd()%n+1,a,b;a=b=x;
	while(true){
		a=f(a,n),b=f(f(b,n),n);
		if(__gcd(abs(a-b),n)>1)return __gcd(abs(a-b),n);
	}
}
signed main(){
    cin>>n;
    int x;
    do x=pollard_rho(n);while(x==n);
    cout<<x;
    return 0;
}