2025.2.21的模拟赛题“樱花树”题解

2025.2.21的模拟赛题“樱花树”题解

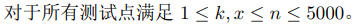
为避免混淆，题目中的 \(X\) 在下文中为大写。

操作标号法，将不同的操作标号，并用无序列表的方式罗列各自的限制，可以使得逻辑清晰

称前 \(k-1\) 次操作成为1号操作，第 \(k\) 次（不含）以后的操作称作2号操作

设 \(f_{x,i,j}\) 表示在 \(x\) 的子树中，1号操作做了 \(i\) 次，2号操作做了 \(j\) 次
限制就是

• \(X\) 到跟的路径不能做1号操作，x的子树中不能做2号操作
• \(X\) 节点本身的操作既不计入1，也不计入2，可以看作不操作
• 子树中执行了2号操作，其到根节点就不能执行1号操作

dp 方程也十分简单了，

\[f_{x,a,b}f_{y,A,B}{a+A\choose a}{b+B\choose b}\to f'_{x,a+A,b+B} \]

这样复杂度 \(\mathcal O(n^3)\)。

考虑优化，令 \(f_{x,i}\) 表示在 \(x\) 的子树中操作 \(i\) 次的方案数，若 \(x\) 是 \(X\) 及其祖先，则强制令其不删除。这个转移是简单的。

将节点分为三类

对于 \(x\) 的子树，可以直接用一个普通的背包求解

对于 \(x\) 外的非祖先，其实也没必要分的那么清楚，可以简单的存个总的操作次数

主要是对于 \(x\) 的祖先，需要把进行了几次 \(x\) 前的操作分出来，但主要对于 \(x\) 外的非祖先也不是那么好分，方案数不定。

我们发现1号操作

一种巧妙地思路是，设 \(g_{x,i}\) 表示从根处理到节点 \(x\) ，其中在 \(x\) 节点之前被选中的节点数有 \(i\) 个的方案数。

首先考虑如何从父亲继承：

\[g_{x,i}=[x\ne 1\land x\ne X]g_{fa,i}+\sum_{j=i}^ng_{fa,j} \]

什么意思呢？

• 首先如果 \(x\) 节点不进行删除操作，那么所有在 \(fa\) 节点之后操作的也会在 \(x\) 节点之后，然而当 \(x=1\ or\ X\) 的时候 \(x\) 必须执行删除操作，所以有 \([x\ne 1\land x\ne X]g_{fa,i}\) 的贡献

• 如果 \(x\) 要执行删除操作，那么对于每一种 \(fa\) 之后的删除节点的操作序列，都可以选择任意多的节点放在 \(x\) 之前删除，其余的放在 \(x\) 之后操作，由于每种操作序列的顺序是确定的，这里不需要乘以组合数，有 \(\sum_{j=i}^ng_{fa,j}\) 的贡献

接下来考虑如何合并 \(x\) 的子树，既然这些节点都在 \(x\) 之后操作了，那么合并就十分简单了，有：

\[g_{x,i}\times f_{x,j}\times {i+j\choose i}\to g'_{x,i+j} \]

于是我们在 \(\mathcal O(n^2)\) 的时间中解决了这道题。

代码（去掉取模了，应该是很好理解的）：

g[0]=1;
for(int x:anc){
    for(int i=all,sum=0;i>=0;i--){
        sum+=g[i];
        g[i]=(x==1||x==u?0:g[i])+sum;
    }
    for(int i=0;i<=all;i++)tmp[i]=g[i],g[i]=0;
    for(int i=0;i<=all;i++)
        for(int j=0;j<=siz[x];j++)
            g[i+j]+=tmp[i]*f[x][j]*c[i+j][i];
    all+=siz[x];
}
cout<<g[K-1];