小郭的矩形
小郭的矩形
——洋葱式推式子+拆组合数递推式子+\({0\choose 0}\) 不能拆+等式两边同时前缀和
题目描述
\[f(i,j)=\begin{cases}p\times f(i-1,j)+q\times (i,j-1)+c&&i\geq1,j\geq1\\a_i&&i\geq1,j=0\\b_j&&i=0,j\geq1\\0&&i=j=0\end{cases}
\]
\[ans=\sum_{i=0}^n\sum_{j=0}^nh^{i(n+1)+j}f(i,j)
\]
求 \(ans\) 对 \(998244353\) 取模的结果。
题解
分别考虑 \(a_i,b_i,c\) 对中心区域的贡献
\(a_i\) 的贡献
\(P=p\times h^{n+1},Q=q\times h,a_i\times h^{i(n+1)}\to a_i\)
形如:
\[\begin{bmatrix}
1&Q&Q^2&Q^3\\
&QP&Q^2P&Q^3P\\
&QP^2&Q^2P^2&Q^3P^2
\end{bmatrix}
\]
所以贡献为:
\[ans=\sum_{x=1}^na_x(1+Q\sum_{i=0}^{n-x}\sum_{j=0}^{n-1}Q^iP^j{i+j\choose i})
\]
令 \(f(x)=\sum_{i=0}^{x}Q^i\sum_{j=1}^{i-1}P^j{i+j\choose i}\),则 \(ans=\sum_{i=0}^na_x(1+Q\times f(n-x))\)
令 \(g(x)=\sum_{j=0}^{n-1}P^j{x+j\choose j}\),则 \(f(x)=\sum_{i=0}^x Q^ig(i)\)
因为:
\[\begin{aligned}
g(x)&=\sum_{i=0}^{n-1}P^i{x+i\choose i}\\
&=\sum_{i=0}^{n-1}P^i({x+i-1\choose i}+{x+i-1\choose i-1})\\
&=\sum_{i=0}^{n-1}P^i{x+i-1\choose i}+P\sum_{i=0}^{n-2}P^i{x+i\choose i}\\
&=g(x-1)+Pg(x)-P^n{x+n-1\choose n-1}\\
\end{aligned}
\]
所以:\(g(x-1)=(1-P)g(x)+P^n{x+n-1\choose n-1}\)。
于是可以 \(\mathcal O(n)\) 求解。
\(b_i\) 的贡献
\(b_i\leftarrow b_i\times h^i\)
形如:
\[\begin{bmatrix}
1&&\\
P&QP&Q^2P\\
P^2&QP^2&Q^2P^2\\
P^3&QP^3&Q^2P^3
\end{bmatrix}
\]
所以贡献为:
\[ans=\sum_{x=1}^nb_x(1+P\sum_{i=0}^{n-1}\sum_{j=0}^{n-x}Q^iP^j{i+j\choose i})
\]
令 \(ans=\sum_{x=1}^nb_x(1+f(n-x)),f(x)=\sum_{j=0}^{n-x}P^jg(j),g(x)=\sum_{i=0}^{n-1}Q^i{i+x\choose i}\)
\[\begin{aligned}
g(x)&=\sum_{i=0}^{n-1}Q^i{i+x\choose i}\\
&=\sum_{i=0}^{n-1}Q^i{i+x-1\choose i}+Q\sum_{i=0}^{n-2}Q^i{i+x\choose i}\\
&=g(x-1)+Qg(x)-Q^n{x+n-1\choose n-1}
\end{aligned}
\]
所以 \(g(x-1)=(1-Q)g(x)+Q^n{x+n-1\choose n-1}\),可以 \(\mathcal O(n)\) 求解。
\(c\) 的贡献
\[ans=\sum_{x=1}^n\sum_{y=1}^nh^{x(n+1)+y}(\sum_{i=0}^{n-x}\sum_{j=0}^{n-y}P^iQ^j{i+j\choose i})
\]
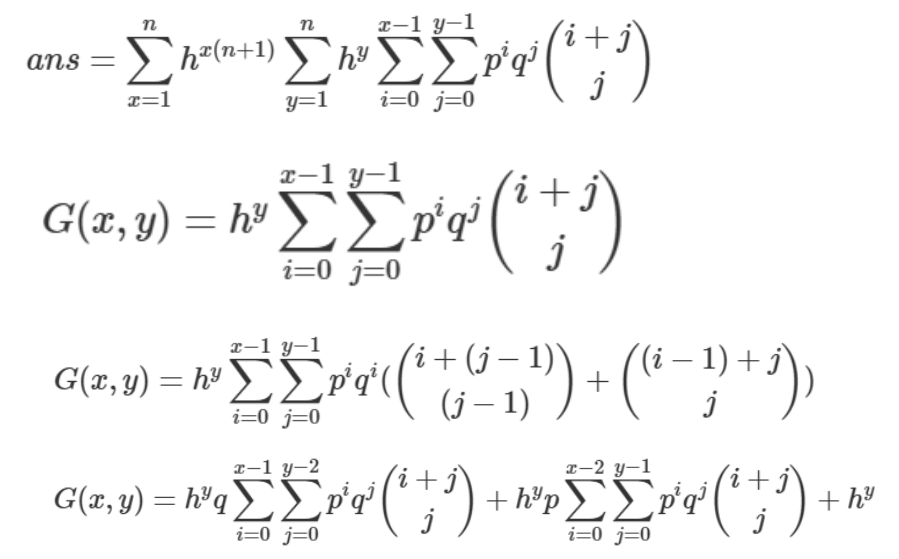
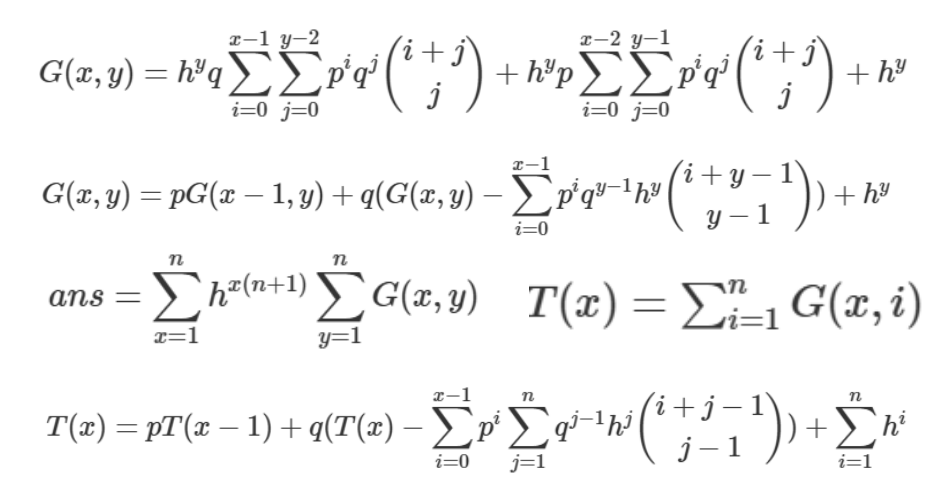
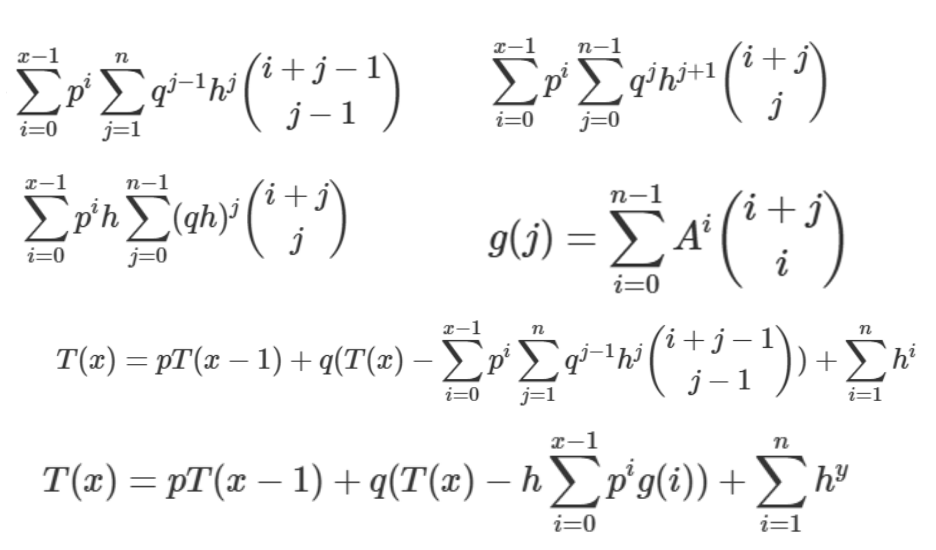


 浙公网安备 33010602011771号
浙公网安备 33010602011771号