博弈论
博弈论学习笔记
基本模型
对于一般博弈论,可以看 APIO2025 刘恒熙的授课《博弈理论入门》。这类游戏在 OI 题中很少出现。但是这东西很强,可以推出公平组合游戏的 SG 函数。
当左右决策不同时,我们将整个博弈看作一棵树。
对于公平组合游戏,将整个博弈过程看作一张DAG。
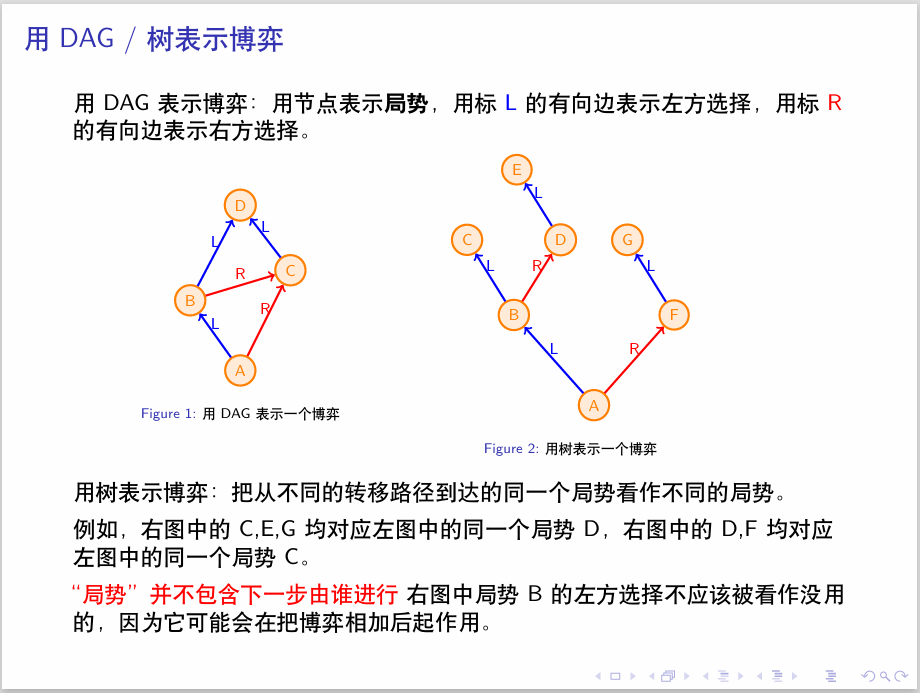
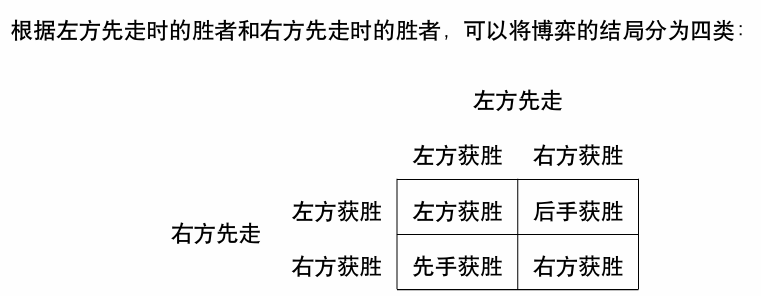

对于任何一个无偏游戏,我们可以通过写下其后继状态来递归确定这个游戏。设 \(x\) 的后继状态为 \(y_1\sim y_k\),则 \(x=\{y_1,y_2,\cdots,y_k\}\)
定义多个游戏的和,表示每次在多个游戏中随便选择一个游戏走一步,知道最后一方不能在任何游戏中行走时判负。
形式化的,游戏 \(x_1\) 与游戏 \(x_2\) 的和定义为:
这是一个递归定义,\(y_{1*}\) 表示 \(x_1\) 的后继游戏,\(y_{2*}\) 表示 \(x_2\) 的后继游戏。
如果两个局面 \(x,y\) 在博弈中行为完全相同,则记作 \(x=y\)。
Nim 博弈
有 \(n\) 个石子堆,第 \(i\) 个石子堆有 \(a_i\) 个,每次从一个石子堆中拿走至少一个石子,无法行动者负。
结论:当且仅当当 \(\bigoplus a_i=0\) 时先手必败。
证明分为三个步骤:
-
当 \(\forall i, a_i=0\) 时,根据定义先手必败,满足结论。
-
当 \(\bigoplus a_i\ne 0\) 一定存在某种移动使得 \(\bigoplus a_i=0\)。
假设 \(\bigoplus a_i=k,k\ne 0\),则我们要把一个状态 \(a_i\) 改作 \(a_i'\) 使得 \(k\oplus a_i\oplus a_i'=0\)。
假设 \(k\) 的最高位为 \(d\),那么一定存在某个 \(a_i\) 二进制下第 \(d\) 位为 \(1\),而 \(a'=a_i\oplus k\) 这一位为 \(0\)。
所以 \(a_i>a_i'\),移动合法。
-
当 \(\oplus a_i=0\) 一定不存在某种移动使得 \(\oplus a_i =0\)。
假设 \(a_i\to a_i'\) 使得 \(\oplus a_i=0\) ,则 \(a_i\oplus a_i'=0\implies a_i=a_i'\),移动不合法。
我们将”有 \(n\) 个石子的一个石子堆“这个状态记作 \(*n\),显然有 \(*n=\{*0,*1,\cdots ,*(n-1)\}\)。称作 nimber。
那么一个 Nim 博弈记作 \(\sum_{i=1}^n*a_i\)。
SG 函数
对于游戏 \(x=\{y_1,y_2,\cdots,y_k\}\) 定义 \(SG\) 函数:
若 \(x\) 无后继,则先手必败,\(SG(x)=0\)。
用 SG 函数表示 Nimber
很明显有 \(SG(*0)=0\),\(SG(*n)=\operatorname{mex}_{i=0}^{n-1}SG(*i)=n\)。
SG 定理
若 \(SG(x)=y\),则 \(x=*y\)。
证明:
设 \(x=\{y_1,\cdots y_k\}\),假设对于 \(\forall i,y_i\) 都满足 SG 定理,现在证明 \(x\) 也满足 SG 定理。
首先如果 \(x\) 走到了一个 \(y_i\) 使得 \(SG(y_i)>SG(x)\) 那么 \(y_i\) 一定可以再走到一个 \(z\) 使得 \(SG(z)=SG(x)\),根据”化简博弈:绕开可逆行动",这样的行动时无意义的,我们可以直接删去。
于是 \(x=\{*0,*1,\cdots,*(SG(x)-1)\}=*SG(x)\)。
这样我们可以通过 \(nimber\) 的性质研究任何博弈的性质。
巴什博弈
一堆石子,共 \(n\) 个两人轮流取走 \([1,m]\) 个石子,无法行动者负。
结论:若 \((m+1)|n\),则先手必败,否则先手必胜。
证明:直接使用 SG 函数:设还剩 \(x\) 个石子的局面为 \(X\)。则:
很明显,当 \((m+1)|n\) 时 \(SG(N)=0\)。
阶梯 Nim
有 \(n\) 堆石子,每次选择一个 \(i\ge 1\),从 \(a_{i+1}\) 移动至少 \(1\) 个石子到 \(a_i\),无法行动者负。
结论:当且仅当 \(\bigoplus_{i=1}^{\lfloor\frac n2\rfloor}a_{2i}=0\),即偶数位置异或和为 \(0\) 时,先手必败。
简要证明:因为不论从奇数堆想偶数堆移动多少,下一手总是可以移动走,回到一个等价的状态,根据”化简博弈:绕开可逆行动",这样的行动时无意义的,我们可以直接删去。
于是就等价于在偶数位置上玩 Nim 博弈。
当然可以用 SG 函数严谨证明,即证明 \(SG(\{a_i\})=\bigoplus_{i=1}^{\lfloor\frac n2\rfloor}a_{2i}\)。
Anti-Nim
有 \(n\) 个石子堆,第 \(i\) 个石子堆有 \(a_i\) 个,每次从一个石子堆中拿走至少一个石子,无法行动者胜。
结论:设 \(k=\max_ia_i,X=\bigoplus a_i\),则先手必败当且仅当 \([k>1]\oplus [X=0]\)。
K-Nim
有 \(n\) 个石子堆,第 \(i\) 个石子堆有 \(a_i\) 个,每次从至少 \(1\) 至多 \(k\) 个石子堆中拿走至少一个石子,无法行动者负。
结论:设每个数第 \(i\) 位的 \(1\) 的个数之和为 \(b_i\),先手必败当且仅当 \(\forall i,(k+1)|b_i\)。
一些解题技巧
假设法
利用了一个公平组合游戏局面不是先手必胜就是先手必败,那么就可以假设一个局面是先手必胜还是先手必败,思考其决策。
例题:2024.7.9T1 在本题中,发现无论去除 1 后的局面是先手必胜还是先手必败,都可以通过相应的决策使得初始局面时先手必胜。
博弈论DP
就是从终态往前推
Game on Sum
题面
Alice 和 Bob 正在玩一个游戏,游戏分为 n 个回合,Alice 和 Bob 要轮流对一个数 x 进行操作,已知这个数初始值是 0。
具体每个回合的行动规则如下:
- Alice 选择一个在区间 [0,k] 之间的实数 t。
- Bob 可以选择让 x 变成 x+t 或者 x−t,但是 Bob 在 n 个回合之内至少选择 m 次让 x 变成 x+t。
Alice想让最终的 x 最大,Bob 想让最终的 x 最小。
已知双方均采用最优策略,求最终的 x 值(对 10^9+7 取模)。
数据范围保证:1≤m≤n≤2000,k≤10^9+7。
题解
CF1628D2 Game on Sum (Hard Version) - 洛谷专栏 (luogu.com.cn)
Alice先走,Bob后走其实就是让最小值最大。
打表看结论
并且博弈论问题如果不是用 DP,那一定是找结论。且数据范围很大时——\(\mathcal O(N)\),一定是找结论。与其观察什么时候先手必胜,不如观察什么时候先手必败,
打表发现先手必败当且仅当 R 与 L 括号匹配。证明方法与 Nim 博弈相同,分为可以到必败态与只能到必胜态。
”还剩 \(n\) 个石子,限制为 \(k\)“的状态记作 \((n,k)\),则可以列出 \(SG\) 函数:
打出 \([SG(n,k)>0]\) 的表为:
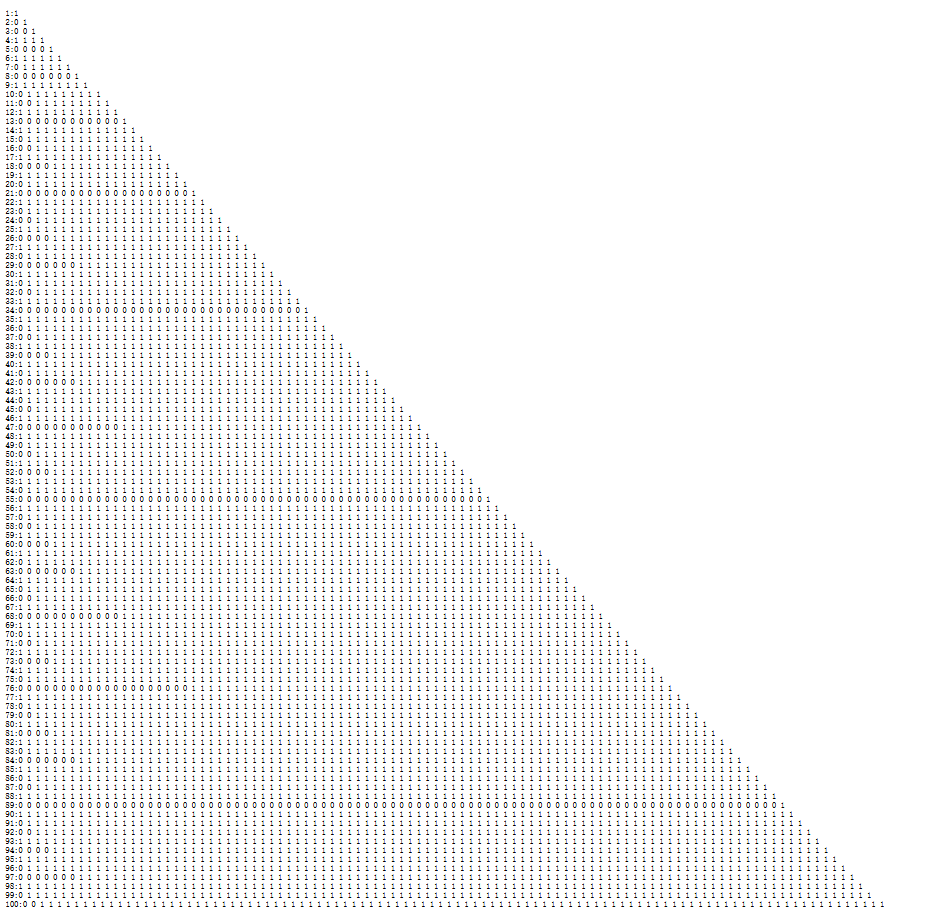
先是发现在斐波那契数处 \(0\) 非常的多,接着发现其他地方 \(0\) 的也和斐波那契数列有关,最终可以得到以下结论:
设正整数 \(n\) 拆成若干个不同的斐波那契数之和后,其中最小的为 \(\tau(n)\) 则 。
于是 \(ans=f(N-1)=\sum_{n=1}^{N-1}[\tau(n)\le k]\),设小于等于 \(n\) 的最大的斐波那契数为 \(x\) 则有 \(f(n)=f(x-1)+f(n-x)+[x\le k]\),计算即可,复杂度 \(\mathcal O(T\log N)\)。
用 \((x,t)\) 表示在 \(x\) 节点上,tax 为 \(t\) 的状态。
从SG函数角度考虑。首先对于一个没有任何出边的点 \(z\),其实等价于一个 Nim 石子堆,即 \(SG(z,t)=t\)。
对于一个直接与叶子 \(z\) 相连的点 \(y\),有:
那么 \(SG(y,1)\) 可以取到无穷大。我们设此时 \(SG(y,1)=\omega\),满足 \(\omega\) 是一个无穷大的量。
对于状态 \((y,t)\),根据定义有:
所以 \(SG(y,t)=t\times \omega=t\omega\)。
对于一个直接与 \(y,z\) 相连的点 \(x\),有:
那么 \(x\) 可以取到 \(\omega\) 个 \(\omega\),于是记 \(SG(x,1)=\omega^2\),同理 \(SG(x,t)=t\omega^2\)。
按照这种规则,我们可以求得每个点的SG函数,然后对其异或后求游戏和。运算规则为:
这是因为不同 \(\omega\) 的次幂之间没有定义 \(\oplus\),所以不能计算。
设最后异或的结果为 \(\bigoplus_i a_i\omega^i\)
于是可以猜测先手必败当且仅当最后的结果 \(=0\),即每一位上的异或和都等于 \(0\)。也十分好证明:
- 对于停止局面,所有城市上的 tax 都等于 \(0\),成立。
- 当 \(\oplus =0\) 时,无论怎么移动,一定会使得 \(\oplus \ne 0\)。
- 当 \(\oplus \ne 0\) 时,取满足 \(a_t\ne 0\) 的最大的 \(t\),用类似 Nim 的方式找到一个对应的点 \(x\),满足 \(SG(x,1)=\omega^t\),首先让他减少为 \(h_x\gets h_x\oplus a_t\),其次考虑每条出边,由于可以到达所有的 \(o\le t\),设 \(x\) 的出点为 \(y\),\(SG(y,1)=\omega^o\)将 \(h_y\gets h_y\oplus a_o\) 即可。注意 \(o\) 相同的 \(y\) 只能取一个。
代码:
#include<bits/stdc++.h>
#define io ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define file(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout)
#define int long long
#define lop(i,a,b) for(int i=a;i<=b;i++)
#define pol(i,a,b) for(int i=a;i>=b;i--)
#define fi first
#define se second
#define mset(a,v) memset(a,v,sizeof a)
#define mcpy(a,b) memset(a,b,sizeof b)
#define umap unordered_map
#define pb push_back
#define pc(x) __builtin_popcountll(x)
using namespace std;
typedef pair<int,int> pa;
typedef vector<int> vi;
const int NN=2e5+5;
int n,m,h[NN];
vector<int> ed[NN];
bool vst[NN];
bool deal[NN];
int bit[NN];//每一位的指数
int a[NN];//异或多项式
int mex(vi v){
sort(v.begin(),v.end());
int cnt=0;
for(int o:v){
if(o<cnt)continue;
if(o!=cnt)return cnt;
cnt++;
}
return cnt;
}
void DFS(int x){
if(vst[x])return;
vst[x]=1;
vi v;
for(int y:ed[x]){
DFS(y);
v.pb(bit[y]);
}
bit[x]=mex(v);
return;
}
int HighBit(int x){
x|=x>>1;
x|=x>>2;
x|=x>>4;
x|=x>>8;
x|=x>>16;
x|=x>>32;
return x-(x>>1);
}
signed main(){
cin>>n>>m;
lop(i,1,n)cin>>h[i];
lop(i,1,m){
int u,v;cin>>u>>v;
ed[u].pb(v);
}
lop(x,1,n)if(!vst[x])DFS(x);
lop(x,1,n)a[bit[x]]^=h[x];
int d=0;
lop(b,0,n-1)d|=a[b]>0;
if(!d){
cout<<"LOSE\n";
return 0;
}
cout<<"WIN\n";
//找到最高位
int hib=0,p=0;
pol(b,n-1,0)if(a[b]){hib=b;break;}
//遍历每个点,找到最高位对应的点
lop(x,1,n){
if(bit[x]!=hib)continue;
if(h[x]&HighBit(a[hib])){p=x;break;}
}
//找到点了
h[p]=h[p]^a[hib];//先减少这个节点使得当前位满足
for(int y:ed[p]){
if(deal[bit[y]])continue;
deal[bit[y]]=1;
h[y]=a[bit[y]]^h[y];//任意改变权值,使得bit[y]为满足限制
}
lop(i,1,n)cout<<h[i]<<" ";
return 0;
}
从理解题意到想出解法再到AC,一共用时:1h29min25s。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号