P3688 [ZJOI2017] 树状数组题解

记录一下做这道题的心路历程，说明在没有事先知道“九条是求成了后缀和”的情况下如何发现，以及解释一些部分分的做法。

sub1,18pts：暴力搜索

无脑枚举，复杂度 $\mathcal O(n^m)$。

代码：

#include<bits/stdc++.h>
#define int long long
#define loop(i,a,b) for(int i=a;i<=b;i++)
#define pool(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
const int NN=1e5+5,MOD=998244353;
int n,m,ac[NN],wa[NN],p[NN];
int QP(int a,int b){
    int c=1;
    for(;b;b>>=1){
        if(b&1)c=1ll*c*a%MOD;
        a=1ll*a*a%MOD;
    }
    return c;
}
void AC_Add(int x){
    for(;x<=n;x+=x&-x)ac[x]^=1;
}
int AC_Ask(int x){
    if(x==0)return 0;
    int sum=0;
    for(;x;x-=x&-x)sum^=ac[x];
    return sum;
}
int AC_Query(int l,int r){
    return AC_Ask(r)^AC_Ask(l-1);
}
void WA_Add(int x){
    for(;x;x-=x&-x)wa[x]^=1;
}
int WA_Ask(int x){
    if(x==0)return 0;
    int sum=0;
    for(;x<=n;x+=x&-x)sum^=wa[x];
    return sum;
}
int WA_Query(int l,int r){
    return WA_Ask(r)^WA_Ask(l-1);
}
struct Oper{
    int op,l,r;
    void read(){
        cin>>op>>l>>r;
    }
}qwq[NN];
int ans[NN];
void DFS(int x,int cnt){
    if(x==m+1)return;
    if(qwq[x].op==2){
        ans[x]=(ans[x]+(AC_Query(qwq[x].l,qwq[x].r)==WA_Query(qwq[x].l,qwq[x].r))*p[cnt])%MOD;
        DFS(x+1,cnt);
    }else{
        loop(i,qwq[x].l,qwq[x].r){
            AC_Add(i),WA_Add(i);
            DFS(x+1,cnt+1);
            AC_Add(i),WA_Add(i);
        }
    }
    return;
}
signed main(){
    cin>>n>>m;
    int cnt=0;
    p[0]=1;
    loop(i,1,m){
        qwq[i].read();
        if(qwq[i].op==1){
            cnt++;
            p[cnt]=1ll*p[cnt-1]*QP(qwq[i].r-qwq[i].l+1,MOD-2)%MOD;
        }
    }
    DFS(1,0);
    loop(i,1,m)if(qwq[i].op==2)cout<<ans[i]%MOD<<"\n";
    return 0;
}

但这份代码并不是一无是处，它可以帮我们对拍，并且我们的思路也将从这开始

sub1~3,48pts：DP

根据上述搜索，我们应该考虑记忆化进行剪枝，发现统计答案的时候只与AC_Query(qwq[x].l,qwq[x].r)==WA_Query(qwq[x].l,qwq[x].r)这个值有关，记为 $d$，所以我们可以考虑将其记录下来，并且注意到各个询问之间是没有关系的，我们可以枚举并分别处理。

对于第 $id$ 个询问，记录 $f_{i}$ 表示进行前 $i$ 次操作后 $d=0$ 的概率， $p$ 表示第 $i$ 个操作对 $d$ 造成变化的概率，则有 $f_{i}=p(1-f_{i-1})+(1-p)f_{i-1}$，那么如何求得 $p$？这就要看九条的错误代码的性质：

我们发现其查询（红色）是从左下到右上，修改（蓝色）是从右下到左上，而这两者相交的充要条件就是蓝色线条的起点在红色线条起点的右边，即如果一个修改操作在一个查询操作的右边，就会产生贡献，那不就是后缀和吗？

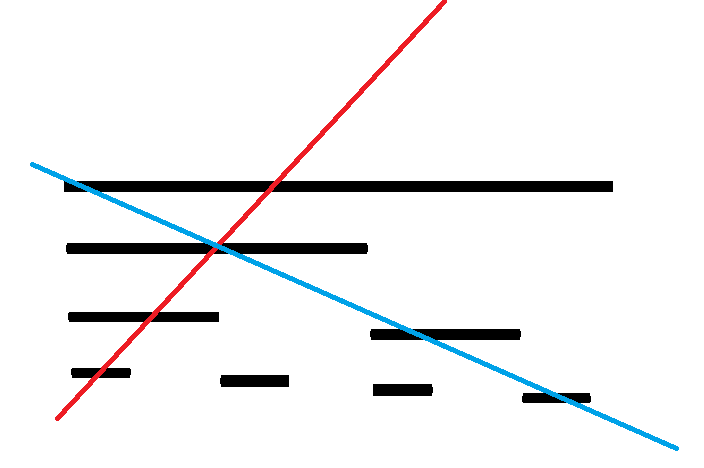
于是 AC_Query 就是查询 $[l,r]$ 的值， WA_Query 就是查询 $[l-1,r-1]$ 的值，那么使得答案不同当且仅当修改了 $l-1,r$ 这两个位置，枚举每个询问，假设包含了 $x$ 个，则 $p=\frac{x}{R-L+1}$。

注意当 $l=1$ 的时候需要特判，此时 AC_Query 查询 $[1,r]$ 的值，WA_Query 查询 $[r,n]$ 的值，那么使得答案不同当且仅当没有修改 $r$，$p=\frac{R-L+1-[L\le r\le R]}{R-L+1}$。

复杂度 $\mathcal O(nm)$。

代码如下：

#include<bits/stdc++.h>
#define loop(i,a,b) for(int i=a;i<=b;i++)
#define pool(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
const int NN=1e5+5,MOD=998244353;
int n,m,f;
int QP(int a,int b){
    int c=1;
    for(;b;b>>=1){
        if(b&1)c=1ll*c*a%MOD;
        a=1ll*a*a%MOD;
    }
    return c;
}
struct Oper{
    int op,l,r;
    void read(){cin>>op>>l>>r;}
}qwq[NN];
struct Seq{int t,l,r;};
vector<Seq> vec_qry;
int ans[NN];
int In(Oper b,int x){return b.l<=x&&x<=b.r;}
int main(){
    cin>>n>>m;
    loop(i,1,m){
        qwq[i].read();
        if(qwq[i].op==2)vec_qry.push_back({i,qwq[i].l,qwq[i].r});
    }
    for(Seq qry:vec_qry){
        f=1;
        loop(i,1,qry.t-1){
            int cnt=0;
            if(qwq[i].op==2)continue;
            if(qry.l!=1)cnt=In(qwq[i],qry.r)+In(qwq[i],qry.l-1);
            else cnt=qwq[i].r-qwq[i].l+1-(qwq[i].l<=qry.r&&qry.r<=qwq[i].r);
            int p=1ll*cnt*QP(qwq[i].r-qwq[i].l+1,MOD-2)%MOD;
            f=(f+p-2ll*p*f%MOD+MOD)%MOD;
        }
        cout<<(f+MOD)%MOD<<"\n";
    }
    return 0;
}

All,100pts：二维线段树

考虑到 $0\le x\le 2$，我们可以直接分类讨论！

$l-1\in [1,L-1],r\in[1,L-1]\cup[R+1,n]\implies p=0$
$l-1\in [1,L-1],r\in[L,R]\implies p=\frac 1{R-L+1}$
$l-1\in [L,R],r\in [L,R]\implies p=\frac2{R-L+1}$
$l-1\in [L,R],r\in [R+1,n]\implies p=\frac 1{R-L+1}$
$l-1\in [R+1,n],r\in [R+1,n]\implies p=\frac 1{R-L+1}$
$l-1=0,r\in [1,L-1]\cup[R+1,n]\implies p=1$
$l-1=0,r\in [L,R]\implies p=\frac{R-L}{R-L+1}$

这就变为了一个二维数点问题。

因为转移 $ \begin{bmatrix}1-p,p\p,1-p\end{bmatrix}\begin{bmatrix}f_{i-1}\1-f_{i-1}\end{bmatrix}=\begin{bmatrix}f_{i}\1-f_{i}\end{bmatrix}$ 形如一个对称矩阵，有结合律，于是可以直接用线段树进行维护。

复杂度 $\mathcal O(m\log^2n)$。

代码如下：

#include<bits/stdc++.h>
#define loop(i,a,b) for(int i=a;i<=b;i++)
#define pool(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
const int NN=1e5+5,MOD=998244353;
int n,m;
int QP(int a,int b){
    int c=1;
    for(;b;b>>=1){
        if(b&1)c=1ll*c*a%MOD;
        a=1ll*a*a%MOD;
    }
    return c;
}
struct SegTr{
    int ls,rs,v;
    #define ls(x) sgt[x].ls
    #define rs(x) sgt[x].rs
    #define v(x) sgt[x].v
}sgt[NN*400];
int rt[NN<<2],tot;
int Mul(int p,int q){return (1-p-q+2ll*p*q%MOD)%MOD;}
void PruneY(int&p,int l,int r,int v,int L=1,int R=n){
    if(l>R||L>r||l>r)return;
    if(!p)p=++tot,v(p)=1;
    if(l<=L&&R<=r){v(p)=Mul(v(p),v);return;}
    int mid=L+R>>1;
    PruneY(ls(p),l,r,v,L,mid);
    PruneY(rs(p),l,r,v,mid+1,R);
    return;
}
void PruneX(int p,int l,int r,int inl,int inr,int v,int L=0,int R=n){
    if(l>R||L>r||l>r)return;
    if(l<=L&&R<=r)return PruneY(rt[p],inl,inr,v);
    int mid=L+R>>1;
    PruneX(p<<1,l,r,inl,inr,v,L,mid);
    PruneX(p<<1|1,l,r,inl,inr,v,mid+1,R);
    return;
}
int PickY(int p,int pos,int L=1,int R=n){
    if(!p)return 1;
    if(L==R)return v(p);
    int mid=L+R>>1;
    if(pos<=mid)return Mul(PickY(ls(p),pos,L,mid),v(p));
    else        return Mul(PickY(rs(p),pos,mid+1,R),v(p));
}
int PickX(int p,int pos,int inpos,int L=0,int R=n){
    if(L==R)return PickY(rt[p],inpos);
    int mid=L+R>>1;
    int tmp=PickY(rt[p],inpos);
    if(pos<=mid)return Mul(PickX(p<<1,pos,inpos,L,mid),tmp);
    else        return Mul(PickX(p<<1|1,pos,inpos,mid+1,R),tmp);
}
int Mod(int p){return (p%MOD+MOD)%MOD;}
signed main(){
    cin>>n>>m;
    loop(i,1,m){
        int op,l,r;cin>>op>>l>>r;
        if(op==1){
            int p=QP(r-l+1,MOD-2);
            PruneX(1,1,l-1,l,r,Mod(1-p)),PruneX(1,0,0,1,l-1,0);
            PruneX(1,l,r,r+1,n,Mod(1-p)),PruneX(1,0,0,r+1,n,0);
            PruneX(1,l,r,l,r,Mod(1-2*p)),PruneX(1,0,0,l,r,p);
        }
        else cout<<Mod(PickX(1,l-1,r))<<"\n";
    }
    return 0;
}

posted @ 2024-09-05 22:16 lupengheyyds 阅读(37) 评论(0) 收藏举报

刷新页面返回顶部

Loading

lupengheyyds

P3688 [ZJOI2017] 树状数组题解

P3688 [ZJOI2017] 树状数组题解

sub1,18pts：暴力搜索

sub1~3,48pts：DP

All,100pts：二维线段树

公告

Loading

lupengheyyds

P3688 [ZJOI2017] 树状数组 题解

P3688 [ZJOI2017] 树状数组 题解

sub1,18pts：暴力搜索

sub1~3,48pts：DP

All,100pts：二维线段树

公告

P3688 [ZJOI2017] 树状数组题解

P3688 [ZJOI2017] 树状数组题解